(1) 囲碁の必勝法
囲碁というゲームは、 局地戦が何箇所かできますので、 常に全体を見ながら進めていかなければなりません。 囲碁の必勝法として 「 両方が先手になるところに打ちなさい、 それも価値の大きいところから。」 という教えがあります。 もし間違って 「 両方が先手になるところ 」 の第3番目に価値の大きいところを打ったとしたら、 相手から 「 両方が先手になるところ 」 の1番目と2番目に大きな価値のところを先手で打たれることになります。 もし 「 両方が先手になるところ 」 が他に少ししかない場合には、 「 相手からは先手になるけれどもこちらからは後手になるところ 」 に打つほうが価値が高くなる場合があり、 そのときには後手になるのを覚悟でそう打たれることもあります。 「 こちらからは先手になるけれども相手からは後手になるところ 」 は、 相手からは 「 両方が先手になるところ 」 がなくならないうちは、 めったに打ってきませんので急ぐことはありません。 コウ争いが起こった時の道具として取っておくべきです。
この手は先手になるのか後手になるのか、 そしてどこが一番価値が高いのか、 それがいつも解っているのなら、 上記の必勝法を守りさえすればいいのですが、 それがいつも解らないから勝ったり負けたりするのです。 それが少しでも解るようになるための訓練法として、 自分が手抜きをしたらどうなるのか、 また相手が手抜きをしたらどうなるのかを考えてから、 次の自分の手を考えるという方法があります。 これを 「 手抜きの仮想法 」 と言うことにします。 もし、 相手が2手続けて同じ局地戦場に打ったために自分が被る被害よりも、 他の 「 両方が先手になるところ 」 の局地戦場で自分が先手をとって得る利害の方が大きいと思うのならば、 その局地戦からは引き上げることです。 また、 もし自分が2手続けて同じ局地戦場に打って得る利益が、 他の 「両方が先手になるところ」 の局地戦場で相手が先手をとったために被る被害よりも少ないと思うのならば、 相手の打った手に対して手を抜くことです。
上手(うわて)と勝負するときは、 上手は上記のことをよくわかっているので 「 上手が打つところは必ず一番価値の高い両方が先手になるところである。」 と決めつけないことです。 勝負が終わった後で上手から褒められるのは、 「 あそこはよく手を抜いたね。」 という場合が多いのです。 上記のような訓練を続けていれば、 きっと上手の打った石のそばしか打てなくなる恐怖から解放されることでしょう。 もちろんそれまでには幾多の失敗をすることとは思いますが、 失敗は成功の基です。
囲碁のゲームの最後に残るのは 「 両方が後手になるところ 」 です。 そこでも、 価値の大きいところから打っていきます。 ゲームの最後のほうはヨセと言われます。 ヨセこそ囲碁の本髄です。 なぜならばヨセこそが囲い合いだからです。 ということは、 ヨセになる前は囲うよりももっと大事なことがあるということです。 どこからがヨセになるのか、 ヨセの最初のほうは大ヨセと言われます。 中盤から終盤の最初の大ヨセに移行するタイミング、 タイミングといってもそれは 「 両方が先手になるところに打ちなさい、 それも価値の大きいところから。」 という原則に従ってゲームを進行させたときに囲い合いになる瞬間のことですが、 それがまた解りにくいのです。 それが少しでも解るようになる訓練法として、 「 手抜きの仮想法 」 とともに 「 出入りの計算 」 があります。 出入り計算とは、 囲い合いをしたときに、 自分からヨセたとき と 相手からヨセたとき の囲う地の差を求めることです。 出入りは、 打つ手の価値の大きさの指標になります。
出入り =
 +
+ 
 ヨセに関係するあるエリアにおいて、 自分からヨセたときの、
ヨセに関係するあるエリアにおいて、 自分からヨセたときの、自分の地から相手の地を引いたもの。
 ヨセに関係するそのエリアにおいて、 相手からヨセたときの、
ヨセに関係するそのエリアにおいて、 相手からヨセたときの、相手の地から自分の地を引いたもの。
ヨセも 「 両方が先手になるところに打ちなさい、 それも価値の大きいところから。」 という原則は同じです。 ヨセでは、 特に 「 両方が先手になるところ 」 が重要ですからそれをとことん優先してください。 次にヨセで大切になるところは、 「 こちらからは先手になるけれども相手からは後手になるところ 」 です。 最後に大切なのは、 「 相手からは先手になるけれどもこちらからは後手になるところ 」 と 「 両方が後手になるところ 」 です。 ただし、 「 相手からは先手になるけれどもこちらからは後手になるところ 」 は実際の出入りを2倍して、 「 両方が後手になるところ 」 の出入りと比較し、 価値の大きいところから着手してください。 なぜなら、 「 相手からは先手になるけれどもこちらからは後手になるところ 」 を1つ潰す(つぶす)ということは、 相手が 「 相手からは先手になるけれどもこちらからは後手になるところ 」 と 「 両方が後手になるところ 」 よりも優先する 「 こちらからは先手になるけれども相手からは後手になるところ 」 を1つ潰すことになるからです。
図1 第1線のヨセ_両先手: 出入り4目
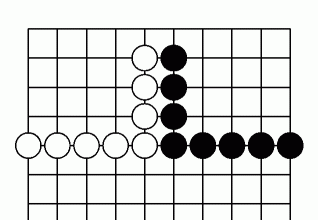
図2 第1線のヨセ_片先手 または 片後手 : 出入り3目
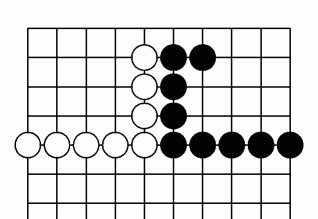
図3 第1線のヨセ_両後手: 出入り2目
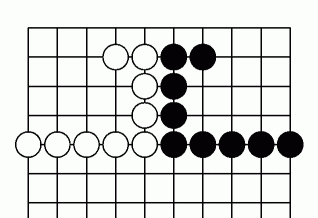
黒の立場からすると、 図1 が両先手、 図2が片先手、 図3が両後手 ですから、 素直に、 図1が最優先、 図2が2番目、 図3が3番目 になります。
白の立場からすると、 図1 が両先手、 図2が片後手、 図3が両後手 ですから、 図1が最優先は当然。 その次は、 後手どうしの出入りを比較して、 図2の出入りは価値にして6目、 図3の出入りは価値にして2目、 ですから、 図2が2番目、 図3が3番目 になります。
(2) 半コウの出入りは 3分の2目
第1線のハネツギの両後手ヨセは 2目 の価値であり、 戸締りが完了する直前の相手の陣地に出るのは 1 目 の価値です。 しかし、 半コウを抜いたりついだりするのはそれよりも価値が低くて、 3分の2目 です。 半コウの出入りを計算してみましょう。
最初の半コウの形 : 半コウは両後手とみなします。
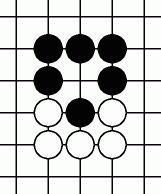
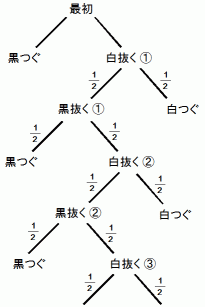
黒先手の場合 :
黒がついでコウを解消することになります。
黒の地 − 白の地 = 0 − 0 = 0
白先手の場合 :
あげはまの数 = 地 になります。
黒がついでコウが解消された場合は、黒と白とであげはまの数は等しくなります。
白がついでコウが解消された場合は、あげはまの数は白が1個多くなります。
黒がコウの場所に2回打ってコウを解消する確率を
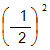 とみなします。
とみなします。黒がコウの場所に3回打ってコウを解消する確率を
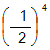 とみなします。
とみなします。黒がコウの場所に4回打ってコウを解消する確率を
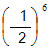 とみなします。
とみなします。白がコウの場所に2回打ってコウを解消する確率を
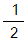 とみなします。
とみなします。白がコウの場所に3回打ってコウを解消する確率を
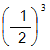 とみなします。
とみなします。白がコウの場所に4回打ってコウを解消する確率を
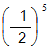 とみなします。
とみなします。白の地 − 黒の地 は次の式で与えられます。
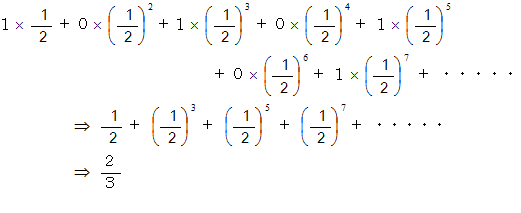
したがって、 出入りは :
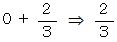
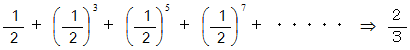 の理由 :
の理由 :その
 : 十進BASIC のプラグラムを用いて概算する
: 十進BASIC のプラグラムを用いて概算するLET U = 0
FOR i = 1 TO 1000
LET U = U + ( 1 / 2 ) ^ ( 2 * i − 1 )
NEXT i
PRINT U
END
その
 :
: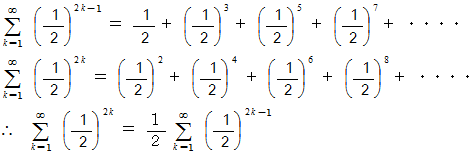
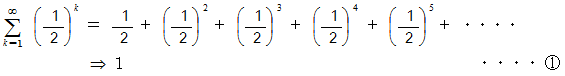
* この式については、 数理論 > 等比数列の無限和 をご覧ください。
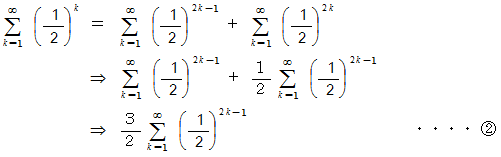
 と
と  より
より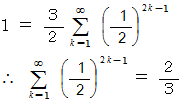
 その他の数学 へ戻る
その他の数学 へ戻る