n を１以上の整数とします。
f (n) を n の多項式で表せば、関数 f (n) がどんな関数であるのかを示したことになります。

（１） 等差数列型漸化式： f (n＋1) ＝ f (n) ＋ q

　　f (n) ＝ f (1) ＋ (n−1) q

　　　　例 ）　f (n＋1) ＝ f (n) ＋ 2　　f (1) ＝ 1　　のとき
　　　　　　　　　f (n) ＝ 1 ＋ 2 (n−1)
　　　　　　　　　数列： f (1)　f (2)　f (3)　f (4)　・ ・ ・
　　　　　　　　　　　　　　　　＝　1　3　5　7　・ ・ ・

（２） 等比数列型漸化式： f (n＋1) ＝ r f (n)

　　f (n) ＝ r ⁿ⁻¹ f (1)

　　　　例 ）　f (n＋1) ＝ 2 f (n)　　f (1) ＝ 1　　のとき
　　　　　　　　　f (n) ＝ 2 ⁿ⁻¹
　　　　　　　　　数列： f (1)　f (2)　f (3)　f (4)　・ ・ ・
　　　　　　　　　　　　　　　　＝　1　2　4　8　・ ・ ・

（３） 階差数列型漸化式： f (n＋1) ＝ f (n) ＋ g (n)

　　n ≧ 2　のとき
　　　　

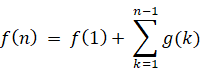
　　　　例 ）　f (n＋1) ＝ f (n) ＋ 2 n　　f (1) ＝ 1　　のとき
　　　　　　　　　f (1) ＝ 1
　　　　　　　　　n ≧ 2　のとき
　　　　　　　　　　　
　　　　　　　　　　　　　　
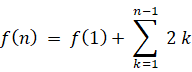
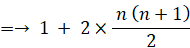
　　　　　　　　　　　　　　＝→　n ²＋n＋1
　　　　　　　　　数列： f (1)　f (2)　f (3)　f (4)　・ ・ ・
　　　　　　　　　　　　　　　　＝　1　3　7　15　・ ・ ・

※ 参考： 大学生のための数学 ＞ 数理論 ＞ 解ける漸化式づくりのための特性方程式