任意の x から y への関数を表す式を とし、 y ＝ x　を として、 これらの式をグラフで表します。
　まず、 ある点 （ x，y ） ＝ （ a ₁ ， ０ ） から出発して y 軸 と平行に移動し、 に突き当たる所まで行きます。 その座標を （ a ₁ ， a ₂ ） とします。 次に、 x 軸 と平行に移動し、 に突き当たる所まで行きます。 その座標は （ a ₂ ， a ₂ ） です。 その次に、 y 軸 と平行に移動し、 に突き当たる所まで行きます。 その座標を （ a ₂ ， a ₃ ） とします。 そのまた次に、 x 軸 と平行に移動し、 に突き当たる所まで行きます。 その座標は （ a ₃ ， a ₃ ） です。　・ ・ ・ ・　というふうに繰り返していくと、 Ａ ：　同じ軌道を通るようになる場合　　　Ｂ ：　原点から果てしなく離れていく場合　　　Ｃ ：　 と のグラフの交点に無限に近づいていく場合　　の３通りあります。 一番目の例としては、 y = −x ＋ ４　があり、 二番目の例としては、 y ＝ ２x − ２　があります。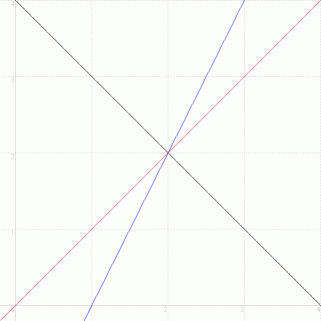

　　　　　　　


今回は Ｃ の場合について考察していくことにしましょう。 まず、 次の式を見てください。
　　　　
次の式を考えます。
　　　　
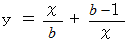
また、次の漸化式を考えます。
　　　　
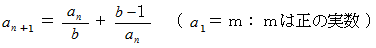
すると、 次の式が成り立ちます。
　　　　
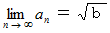
なぜなら、 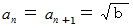だからです。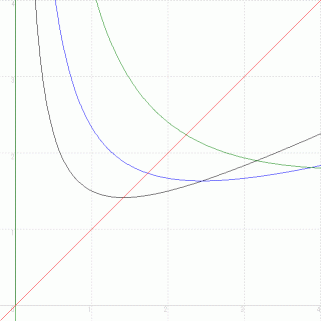

　　　　　　　


　 この原理をプログラムで利用することによって、 いろんな自然数の正の平方根の近似値を求めることができます。

の平方根　

近似値に漸近 ：

　２ の正の平方根　≒　1.4142135623730950・・・
　３ の正の平方根　≒　1.7320508075688772・・・
　５ の正の平方根　≒　2.2360679774997896・・・
　７ の正の平方根　≒　2.6457513110645905・・・

　　プログラムの内容 ：