自然対数の底である ネイピア数を
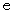 とすると、
とすると、 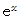 のマクローリン展開式に
のマクローリン展開式に 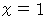 を代入して、 次の式を得ることができます。
を代入して、 次の式を得ることができます。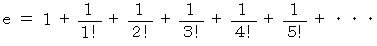
この式は、 次のように書いた方が美しいと言われます。
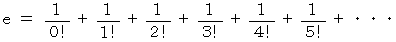
「 えっ! 嘘でしょう。 そしたら
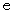 は無限大になっちゃうよ。
は無限大になっちゃうよ。 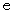 は およそ
は およそ 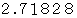 の無理数なんだから。」 と、 そう考えていらっしゃる貴方。 実は、 なんと
の無理数なんだから。」 と、 そう考えていらっしゃる貴方。 実は、 なんと 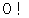 は
は  ではなく
ではなく  なのです。
なのです。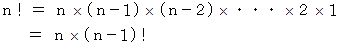
この式に
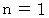 を代入すると、
を代入すると、 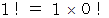 となり、
となり、 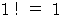 なので
なので 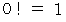 になります。
になります。 数理論 へ戻る
数理論 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る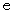 とすると、
とすると、 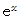 のマクローリン展開式に
のマクローリン展開式に 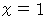 を代入して、 次の式を得ることができます。
を代入して、 次の式を得ることができます。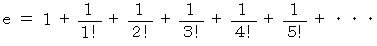
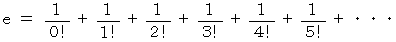
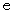 は無限大になっちゃうよ。
は無限大になっちゃうよ。 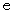 は およそ
は およそ 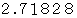 の無理数なんだから。」 と、 そう考えていらっしゃる貴方。 実は、 なんと
の無理数なんだから。」 と、 そう考えていらっしゃる貴方。 実は、 なんと 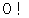 は
は  ではなく
ではなく  なのです。
なのです。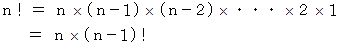
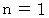 を代入すると、
を代入すると、 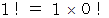 となり、
となり、 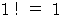 なので
なので 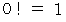 になります。
になります。