世界地図が書かれたビーチボールを２つ用意してください。 まず１つ目のビーチボールから。 呼気の代わりに湯に溶解した天草(あまくさではありません）を注入して膨らませたら、 水につけて冷やし、 ところてん にします。 （ ちなみに、 ところてんを凍結乾燥すると寒天になります。） そうしたら赤道面に平行に１センチメートル間隔でスライスしていきます。 スライスしても切断面がずれないように注意してください。 続いて、 北極点から南極点に向かって東経180度 （ 西経180度 ） の経線をカッターナイフで切り裂いてください。 そして、 ところてんから切断された地図の部分部分をはぎ取って、 平面上に配置して、 北極点が最上になるようにして地図を再構築してください。 次に２つ目のビーチボールです。 １つ目のビーチボールとやり方はほとんど同じです。 ただ、 赤道面に平行に１ナノメートル間隔でスライスするところが違うだけです。

　 ２つ目のビーチボールからできた平面地図は、 長半径と短半径が 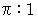の横長の楕円形をしています。 ビーチボールの半径を とし、 その平面地図の赤道を 軸 とし、 東経０度 西経０度 ）の経線を 軸 とすると、 その平面地図の形を表す式は次のようになります。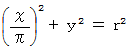
　　　　　
　 ビーチボールの中心から極に向かってビーチボールの半径の 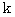倍 だけ離れたところでスライスされた円形面の円周の長さは 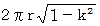だからです。 　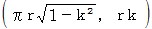は上記の式で表される楕円上の点になります。

　 元々のビーチボール上の 東経180度・北緯０度 の点は、 平面地図では 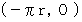と 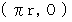の２つの点になっています。 では、 元々のビーチボール上の 東経Ａ度・北緯Ｂ度 の点は、 平面地図ではどんな座標になっているでしょうか？

　 答え ：

　　　　　

　 解説 ：

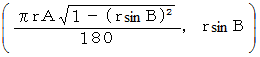
　 次の図を見ると、 北緯Ｂ度の点は 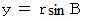になっていることがわかります。
　　　　　

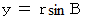　 のとき、 楕円内は　　になっていますから、 東経Ａ度の点は次のようになります。
　　　　　

　 残念ながら、 このような世界地図はこの世に出回っていません。 それは極に近づくほど面積が過小表現されるからです。 極に近づくほど 軸方向の間隔が過小表現されるのです。 これは、 長方形のメルカルト図法による世界地図とは反対です。 そこで、 軸座標を変更して次のような座標に変換します。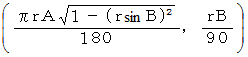
　　　　　
　 こうして長半径と短半径が 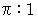の横長の楕円形をした面積誤差の少ない世界地図が出来上がりました。 なお、 現在出回っている面積どおりに表現されている世界地図は、 モルワイデ図法によるもので、 それは、 長半径と短半径が２対１の横長の楕円形をしています。