(14) 時間の基底が虚数であることを忘れていませんか
今までは、 時間を実数とする時空間で考えてきましたが、 相対性理論が扱っているミンコフスキー時空間は、 時間が虚数なのです。 したがって、 本当のローレンツ変換は直交直線座標系から斜交直線座標系への座標変換ではなく、 直交直線座標系から直交直線座標系への座標変換であり、 位置ベクトルの大きさを変えない等長変換なのです。 そのことを見ていくことにしましょう。
1次元虚数時間と1次元空間が直交する2次元ミンコフスキー時空間の基底 :
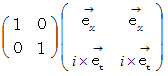
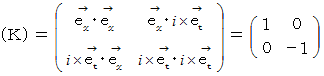


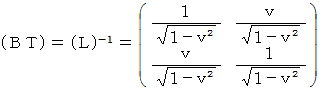
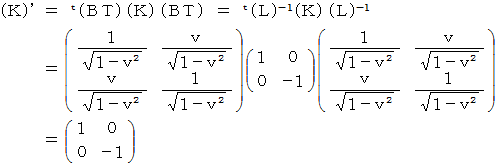
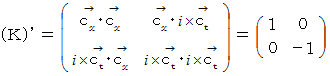
この式から、 ローレンツ変換後の基底が生成する時空間は直交座標
系であることがわかります。
というと、 ローレンツ変換後の基底は、 直交座標系の時間軸と空間
軸が近づくようにそれぞれ
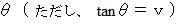 ずつ回転してい
ずつ回転しているのだから、 直交座標系であるわけがないだろうと思われるかもしれ
ませんが、 虚数角の回転ですので、 そうなるのです。
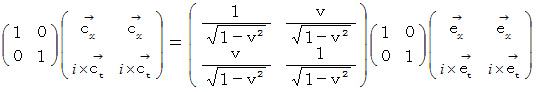
したがって、
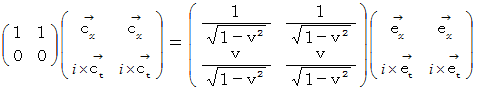
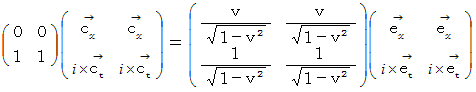
 のローレンツ変換 :
のローレンツ変換 :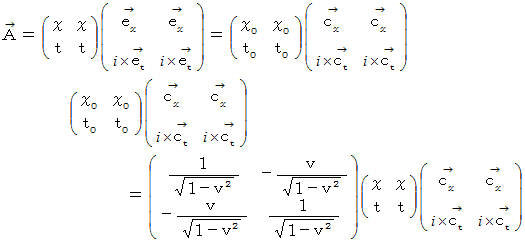

 の大きさ :
の大きさ :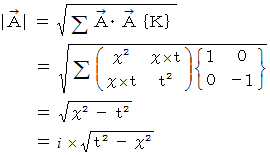
ローレンツ変換後の位置ベクトル
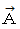 の大きさ :
の大きさ :

 前ページへ戻る
前ページへ戻る