目 次
(1) 物質の移動についての座標変換(2) 物質の出来事についての座標変換( 双子のパラドックス )
(3) 物質の姿についての座標変換
(4) 今日の特殊相対性理論に対する批判
(5) ニュートン力学的観察 と 相対論的観察 を結ぶ 固有時間不変の定理
(6) 4次元時空間距離を不変にする座標変換
(7) ベクトルの座標変換で考える同時刻の相対性
(8) 特殊相対性理論の守備範囲
(9) これまでのまとめ
(10) トンネルと列車のパラドックス
(11) ガリレイ変換とローレンツ変換とでの変換後の基底の比較
(12) 逆ガリレイ変換とローレンツ収縮でローレンツ変換を作る
(13) 方眼紙にローレンツ変換の図を作成してみよう
(14) 時間の基底が虚数であることを忘れていませんか
大学生のための数学 > 線形代数学 > 位置ベクトルの座標変換
(1) 物質の移動についての座標変換
直交座標系から斜交座標系へのベクトルの座標変換の1例として、 「 ローレンツ変換 」 があります。 今は、 光の速さを
 とする単位系で考えることにします。 ある慣性系が他の慣性系に対して速さ
とする単位系で考えることにします。 ある慣性系が他の慣性系に対して速さ  で等速直線運動しています。 図-1 を見てください。 E,C,D の空間を次のようにします。
で等速直線運動しています。 図-1 を見てください。 E,C,D の空間を次のようにします。E 時空間座標系 : ローレンツ変換前の直交直線座標系
 が生成するベクトル空間
が生成するベクトル空間
C 時空間座標系 : ローレンツ変換後の斜交直線座標系
 が生成するベクトル空間
が生成するベクトル空間
E 時空間慣性系に対して、 速さ  で等速直線運動している慣性系
で等速直線運動している慣性系

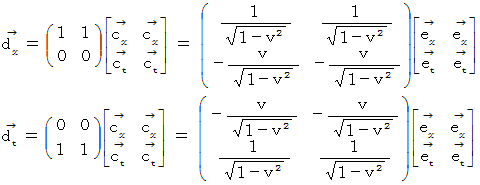
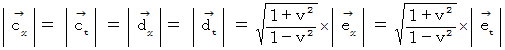
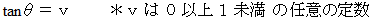
ローレンツ変換 の2つのモデルケースたち :
E 時空間座標系の中での 物質C と 光 の移動
物質C ( 空間移動の速さ
 ; 時空間移動の方向
; 時空間移動の方向 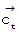 )
)光 ( 空間移動の速さ
 ; 時空間移動の方向
; 時空間移動の方向 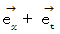 )
)
C 時空間座標系の中での 物質C と 光 の移動
物質C ( 空間移動の速さ
 ; 時空間移動の方向
; 時空間移動の方向 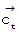 )
)光 ( 空間移動の速さ
 ; 時空間移動の方向
; 時空間移動の方向 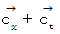 )
)光の速さを  とする単位系では、ローレンツ変換テンソル
とする単位系では、ローレンツ変換テンソル
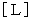 の表現行列は、 次のように表されます。
の表現行列は、 次のように表されます。
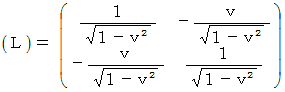
したがって、
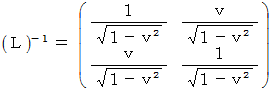
 物質C の時空間移動についてのローレンツ変換
物質C の時空間移動についてのローレンツ変換静止している観察者 ( 第1観察者 ) の座標系での物質C の時空間移動 ( 直交座標系 )
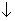
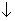
その観察者が観察する、 物質C に並走して移動している観察者 ( 第0観察者 ) の座標系での物質C の時空間移動 ( 斜交座標系 )
つまり、
第1観察者による、 物質C の時空間移動についての、 第3者的な主観的観察
( ただし、 物質C の速度は、 当事者的な主観的観察になります。)
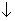
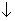
第1観察者による、 第0観察者の物質C の時空間移動についての当事者的な主観的観察についての、 当事者的な客観的観察
( つまり、 第1観察者による、 物質C の時空間移動についての、 当事者的な客観的観察 )
* コメント
当事者的な観察 : 観察の対象となる物質が静止している。
ただし、 速度については、 移動している物質ではなくて、
その基準になる物質が静止している場合は、 当事者的な
観察になります。
第3者的な観察 : 観察の対象となる物質が移動している。
主観的な観察 : 観察者が携帯している時計や物差しを使用する。
客観的な観察 : 観察している物質が携帯している時計や物差しを使用する。

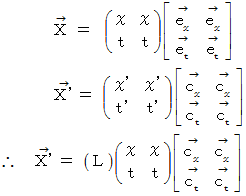
 物質Cの時空間移動 についての 逆ローレンツ変換
物質Cの時空間移動 についての 逆ローレンツ変換静止している観察者が観察する、 物質C に並走して移動している観察者の座標系での物質C の時空間移動 ( 斜交座標系 )
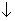
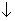
静止している観察者の座標系での物質C の時空間移動 ( 直交座標系 )
つまり、
第1観察者による、 第0観察者の物質C の時空間移動についての当事者的な主観的観察についての、 当事者的な客観的観察
( つまり、 第1観察者による、 物質C の時空間移動についての、 当事者的な客観的観察 )
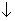
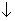
第1観察者による、 その物質の時空間移動についての、 第3者的な主観的観察
( ただし、 物質C の速度は、 当事者的な主観的観察になります。)
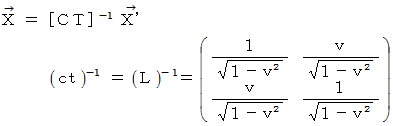

さて、 位置ベクトル 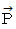 があり、 それは E 時空間では次のように表されるものとします。
があり、 それは E 時空間では次のように表されるものとします。
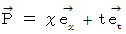
位置ベクトル 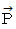 の E 時空間における大きさは
の E 時空間における大きさは 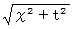 です。
です。
位置ベクトル 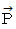 は C 時空間では、 次のように表されます。
は C 時空間では、 次のように表されます。
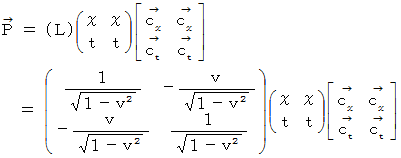
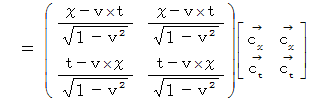
位置ベクトル 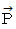 の C 時空間での大きさを求めてみましょう。
の C 時空間での大きさを求めてみましょう。
以下の式が求める答えであるとしてはいけません。
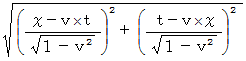
なぜならば、 それは、 位置ベクトル 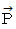 の C 時空間での表示をわざわざ E 時空間に移植して E 時空間でその大きさを測定しているからです。
の C 時空間での表示をわざわざ E 時空間に移植して E 時空間でその大きさを測定しているからです。
斜交座標系でのベクトルの大きさを求めるためには、 次の式たちのどちらかを使用しなければなりません。
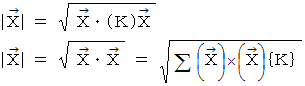
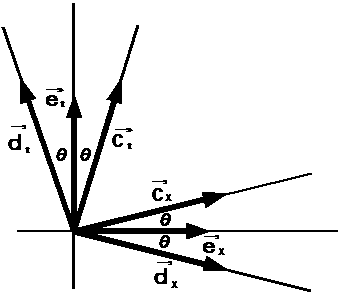
どちらの式を用いるにしても 「 計量テンソル 」 が必要になります。 その 「 計量テンソル 」 の求め方には、 2通りあります。 1番目の計量テンソルの求め方は、 図-2 の幾何学的方法です。
図-2

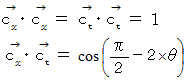
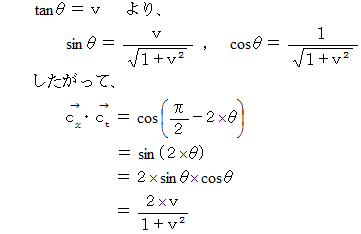
したがって、 座標変換後の斜交座標系の計量テンソルの表現行列は次のようになります。
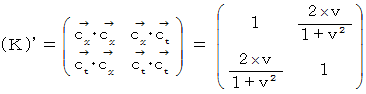
2番目の計量テンソルの求め方は、 計量テンソルの座標変換式を用いるものです。
ローレンツ変換前の時空間の計量テンソルの表現行列は単位行列です。 ローレンツ変換後の時空間の計量テンソルの表現行列を 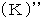 とすると、 次の式が成り立ちます。
とすると、 次の式が成り立ちます。

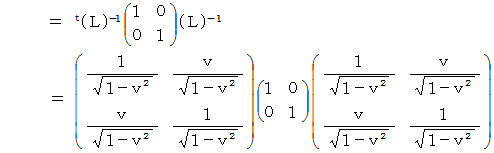
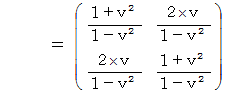
さて、 ここで注意しなければならないことがあります。 それは、 この場合の計量テンソルは、 直交直線座標系の自然基底の要素たちの大きさを  とする基準による計量テンソルになっているということです。 そこで、 これをローレンツ変換後の基底の要素たちの大きさを
とする基準による計量テンソルになっているということです。 そこで、 これをローレンツ変換後の基底の要素たちの大きさを  とする基準による計量テンソルに変換する必要があります。 直交直線座標系の自然基底の要素たちの大きさを
とする基準による計量テンソルに変換する必要があります。 直交直線座標系の自然基底の要素たちの大きさを  とする基準によると、 次の式が成り立ちます。
とする基準によると、 次の式が成り立ちます。
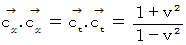
したがって、 この場合の計量テンソルの表現行列
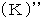 を
を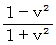 倍してやる必要があります。したがって、 ローレンツ変換後の基底の要素たちの大きさを
倍してやる必要があります。したがって、 ローレンツ変換後の基底の要素たちの大きさを  とする基準による計量テンソルは次のようになります。
とする基準による計量テンソルは次のようになります。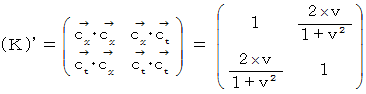
では、 まず、 次の式を用いて位置ベクトル
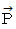 のC時空間での大きさを求めてみましょう。
のC時空間での大きさを求めてみましょう。
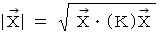
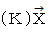 は、 反変ベクトル表示を共変ベクトル表示に換える演算です。
は、 反変ベクトル表示を共変ベクトル表示に換える演算です。

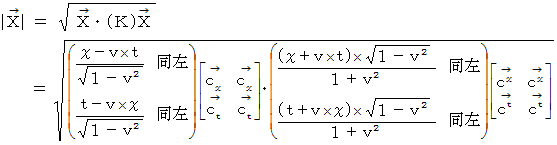
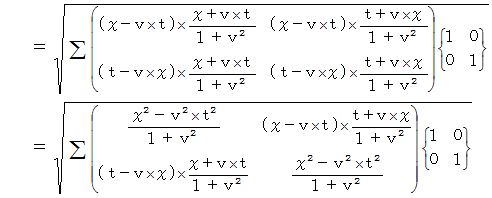
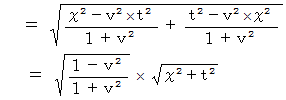
次に、 次の式を用いて位置ベクトル 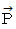 のC時空間での大きさを求めてみましょう。
のC時空間での大きさを求めてみましょう。
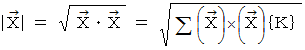
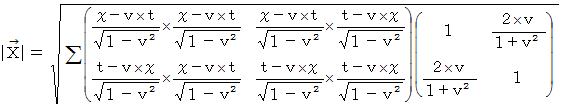
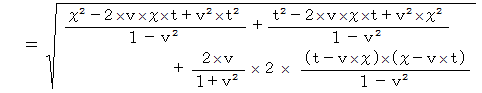
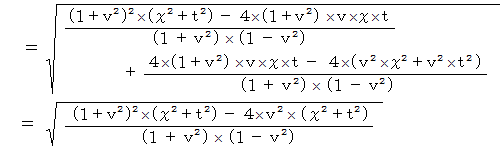
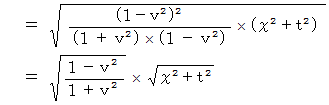
ローレンツ変換に限らず一般の座標変換では、 位置ベクトルの大きさの表現方法は変化するものの、 それは基底の要素たちの大きさや向きが変化したために起きる現象であって、 実質的な位置ベクトルの大きさは変化しません。 それもそのはず、 ベクトル空間の座標変換とは、 同一ベクトルの2つの異なるベクトル空間における表示形式の違いを見るものだからです。 ( この事実を  とします。)
とします。)
しかし、 このことから 「 ローレンツ変換によって時間が収縮したり空間が伸展したりするというのは、 単位の変化を忘れたことによる、 間違いである。」 という結論を導き出すことは間違っています。 なぜなら、 ローレンツ変換により、 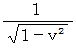 倍に伸びていた時間が元に縮む割合は
倍に伸びていた時間が元に縮む割合は  倍であり、
倍であり、  倍に縮んでいた空間が元に伸びる割合は
倍に縮んでいた空間が元に伸びる割合は 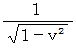 倍であり、 基底の要素たちが大きくなる割合は
倍であり、 基底の要素たちが大きくなる割合は 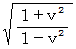 倍であり、 基底の要素たちの大きさの変化率と時間の収縮率や空間の伸展率との積が
倍であり、 基底の要素たちの大きさの変化率と時間の収縮率や空間の伸展率との積が  にならないからです。
にならないからです。
* 移動している慣性系の時間は伸びており ( 時がゆっくり経過しており )、
移動している慣性系の空間は縮んでいます。

ローレンツ変換は、 次のような性質を持つベクトル空間の座標変換です。
 4次元時空間 ( 今は、 簡略化のため、 空間を1次元として考えています。)
4次元時空間 ( 今は、 簡略化のため、 空間を1次元として考えています。)
 直交直線座標系から斜交直線座標系への変換
直交直線座標系から斜交直線座標系への変換
 基底の要素たちの大きさが一様に変化する。
基底の要素たちの大きさが一様に変化する。
 変換前の座標系での位置ベクトル表示に用いられる数値を
変換前の座標系での位置ベクトル表示に用いられる数値を  と
と  とし、
とし、
変換後の座標系での位置ベクトル表示に用いられる数値を 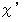 と
と 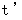 とすると、
とすると、
次の式が成り立つ。 これは 「 固有時間不変の法則 」 と言われる。
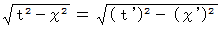
ローレンツ変換で不変なもの、  と
と  の意味を考えましょう。
の意味を考えましょう。
 実質的な位置ベクトルの大きさ :
実質的な位置ベクトルの大きさ : 
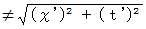
これは、 2つの座標系で観察開始から観察終了までに物質の状態の変化が同一であるということを表しています。
 固有時間 :
固有時間 : 

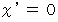 のとき
のとき 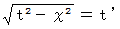 なので、 ローレンツ変換後に静止している慣性系の時間に相当する、 ローレンツ変換で不変なものです。 ローレンツ変換前に速さ
なので、 ローレンツ変換後に静止している慣性系の時間に相当する、 ローレンツ変換で不変なものです。 ローレンツ変換前に速さ  で移動している慣性系の時間が
で移動している慣性系の時間が  で、 移動する距離が
で、 移動する距離が  です。
です。
 なので、 ローレンツ変換前に速さ
なので、 ローレンツ変換前に速さ  で移動している慣性系は、 ローレンツ変換後に時間が収縮している ( 例えば、 元来は60秒経過しているものが、 50秒しか経過していないことになっている。) ことがわかります。
で移動している慣性系は、 ローレンツ変換後に時間が収縮している ( 例えば、 元来は60秒経過しているものが、 50秒しか経過していないことになっている。) ことがわかります。
 ばいおりんのその他の相対論関連論文集 へ戻る
ばいおりんのその他の相対論関連論文集 へ戻る