(13) 方眼紙にローレンツ変換の図を作成してみよう
考えやすくするため、 空間が1次元の、 2次元時空間を考えます。
ある時空点を位置ベクトル
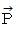 で表すことにします。
で表すことにします。 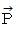 のローレンツ変換前の直交座標系での座標を
のローレンツ変換前の直交座標系での座標を 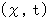 とし、
とし、 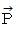 のローレンツ変換後の斜交座標系での座標を
のローレンツ変換後の斜交座標系での座標を 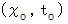 とします。
とします。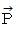 の客観的な大きさを
の客観的な大きさを 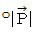 とし、
とし、 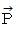 のローレンツ変換前の直交座標系における大きさを
のローレンツ変換前の直交座標系における大きさを 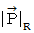 とし、
とし、 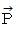 のローレンツ変換後の斜交座標系における大きさを
のローレンツ変換後の斜交座標系における大きさを 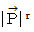 とします。
とします。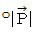 はローレンツ変換にて不変で、 次の式が成り立ちます。
はローレンツ変換にて不変で、 次の式が成り立ちます。
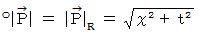
また、 ローレンツ変換ですので、 次の式が成り立っています。
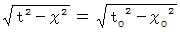
自転しながら速さ
 で等速直線運動 ( 静止を含む ) をしている物質が、 1自転したときの時空間移動を、 時空原点を起点とする位置ベクトル
で等速直線運動 ( 静止を含む ) をしている物質が、 1自転したときの時空間移動を、 時空原点を起点とする位置ベクトル  で表すことにします。
で表すことにします。  のローレンツ変換前の直交座標系における座標を
のローレンツ変換前の直交座標系における座標を  とし、
とし、 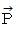 のローレンツ変換後の斜交座標系における座標を
のローレンツ変換後の斜交座標系における座標を 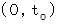 とします。
とします。すると、 次の式たちが成り立ちます。
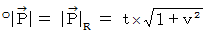
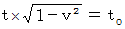 ( 固有時間不変の法則より )
( 固有時間不変の法則より ) )が命ですから、
)が命ですから、  を用いて座標値を表します。
を用いて座標値を表します。 直交座標系で、 位置ベクトル
直交座標系で、 位置ベクトル 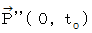 を描きます。
を描きます。* 最初にこうするのは、 「 第0観察者の物質についての当事者的な主観的
観察 」 を意識化するためです。
 次に、 この位置ベクトル
次に、 この位置ベクトル 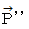 を
を 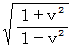 倍 した写像を描きます。
倍 した写像を描きます。すると、 この位置ベクトルは
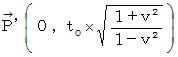 になります。
になります。*
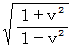 は、 ローレンツ変換では変換後の斜交座標系の基底が変換
は、 ローレンツ変換では変換後の斜交座標系の基底が変換前の直交座標系の基底の
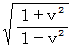 倍になっていることに由来します。
倍になっていることに由来します。 その次に、 その位置ベクトル
その次に、 その位置ベクトル 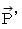 を時計回りに
を時計回りに 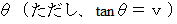 回転させた写像
回転させた写像 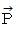 を描きます。 コンパスが必要です。
を描きます。 コンパスが必要です。すると、 この位置ベクトルは
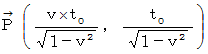 になります。
になります。 この位置ベクトル
この位置ベクトル 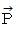 が、 第1観察者 { 第1観察者 は 第0観察者 ( 第0観察者は物質に対して静止しています。) に対して速さ
が、 第1観察者 { 第1観察者 は 第0観察者 ( 第0観察者は物質に対して静止しています。) に対して速さ  で移動しています。} の観察する、 物質が1自転したときの時空間移動になります。 この位置ベクトル
で移動しています。} の観察する、 物質が1自転したときの時空間移動になります。 この位置ベクトル 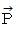 について、 第1観察者の座標系 から 第1観察者が観察する第0観察者の座標系 へのローレンツ変換をします。 第1観察者が観察する第0観察者の座標系は斜交座標系です。 その中身は、 第1観察者が観察する、 物質の立場に立った、 物質の時空間移動と活動になっています。
について、 第1観察者の座標系 から 第1観察者が観察する第0観察者の座標系 へのローレンツ変換をします。 第1観察者が観察する第0観察者の座標系は斜交座標系です。 その中身は、 第1観察者が観察する、 物質の立場に立った、 物質の時空間移動と活動になっています。ローレンツ変換前 ( 直交座標系表示 ) :

ローレンツ変換後 ( 斜交座標系表示 ) :
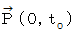
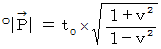 です。
です。 です。
です。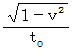 であり、 ローレンツ変換後の第1観察者の物質の立場に立った相対論的観察による物質の自転スピード
であり、 ローレンツ変換後の第1観察者の物質の立場に立った相対論的観察による物質の自転スピード 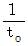 に比べて
に比べて 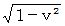 倍 遅くなっています。 もちろんニュートン力学的観察は正しくありません。 しかし、 ニュートン力学的観察 と 相対論的観察 とを比べて、 「 移動している物質の活動スピードは、 移動していないときに比べて遅くなっている。」 と定説は結論づけます。
ローレンツ変換後の第1観察者の物質の立場に立った相対論的観察 ( 第1観察者の物質についての当事者的な客観的観察 ) に対応する 第0観察者の物質の立場に立った相対論的観察 ( 第0観察者の物質についての当事者的な主観的観察 ) では、 この物質の位置ベクトルは、 直交座標系で
倍 遅くなっています。 もちろんニュートン力学的観察は正しくありません。 しかし、 ニュートン力学的観察 と 相対論的観察 とを比べて、 「 移動している物質の活動スピードは、 移動していないときに比べて遅くなっている。」 と定説は結論づけます。
ローレンツ変換後の第1観察者の物質の立場に立った相対論的観察 ( 第1観察者の物質についての当事者的な客観的観察 ) に対応する 第0観察者の物質の立場に立った相対論的観察 ( 第0観察者の物質についての当事者的な主観的観察 ) では、 この物質の位置ベクトルは、 直交座標系で 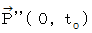 と表されます。
と表されます。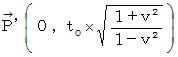 ではありません。
ではありません。第0観察者の相対論的観察による物質の自転スピードは
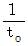 です。 第1観察者の相対論的観察から、 第0観察者の相対論的観察に変更しても、 物質の自転スピードは不変です。 この、 第1観察者の相対論的観察から、 第0観察者の相対論的観察へ変更 ( 写像でも座標変換でもない変換 ) こそ、 相対性理論がまとめるべき結論であると考えます。
です。 第1観察者の相対論的観察から、 第0観察者の相対論的観察に変更しても、 物質の自転スピードは不変です。 この、 第1観察者の相対論的観察から、 第0観察者の相対論的観察へ変更 ( 写像でも座標変換でもない変換 ) こそ、 相対性理論がまとめるべき結論であると考えます。相対性理論において、 時間の長さを比較すべき対象は、 ローレンツ変換の前後ではなくて、 斜交座標系における位置ベクトル
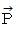
 と 直交座標系における位置ベクトル
と 直交座標系における位置ベクトル 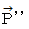
 であると、 考えます。 相対論的な座標変換は、 斜交座標系における位置ベクトル
であると、 考えます。 相対論的な座標変換は、 斜交座標系における位置ベクトル 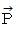
 から 直交座標系における位置ベクトル
から 直交座標系における位置ベクトル 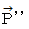
 への時間の不変を内包するような座標変換であるべきだと、 考えます。
への時間の不変を内包するような座標変換であるべきだと、 考えます。 次のページへ進む
次のページへ進む