（２） 物質の出来事についての座標変換（ 双子のパラドックス ）

　 思い浮かべてください。 今、 Ｅ 時空間座標系の中で、 物質Ｃ が速さ で等速直線運動しながら時空間を移動しています。 物質Ｃ には、 別の場所から飛んできた量子が衝突します。 観察が開始されてから量子に衝突するまでに物質Ｃ は１回転します。 その間の物質Ｃ の時空間移動を図で表しながら、 座標変換を考えてみましょう。


　Ｅ 時空間座標系における 物質Ｃ と 反物質Ｃ' の観察とは、
　　　　　　　　　　　　　＊　「 反物質 」 という言い方は、 間違っているかもしれません。
言葉で表すと、
　 （ Ｅ 時空間座標系の観察者を第１観察者と呼び、 Ｃ 時空間座標系の観察者を第０観察者と呼ぶことにする。）
　　　「 第１観察者による、 物質Ｃの出来事についての、 第３者的な主観的観察 」
になります。

図で表すと、 次のようになります。 直交座標系です。

　　　　



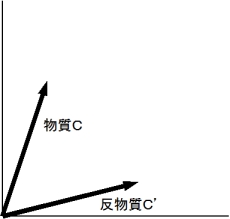
　Ｃ 時空間座標系における 物質Ｃ と 反物質Ｃ' の観察とは、

言葉で表すと、
　　　「 第１観察者による、 物質Ｃの出来事についての、 当事者的な客観的観察 」
になります。

図で表すと、 次のようになります。 斜交座標系です。

　　　　



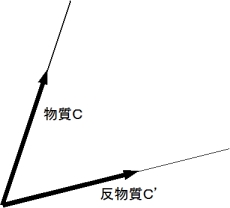
Ｅ 時空間座標系 から Ｃ 時空間座標系 への座標変換は、 次のようになります。

物質Ｃ の位置ベクトル のローレンツ変換 ：
　　

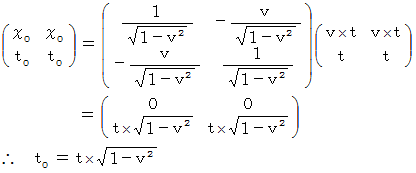
反物質Ｃ' の位置ベクトル のローレンツ変換 ：
　　

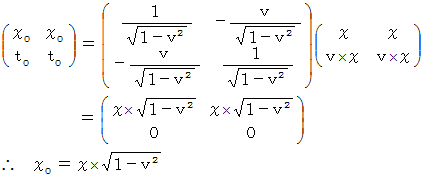
　 したがって、 「 ローレンツ変換によって、 物質や反物質が移動している空間も時間も収縮し、 逆ローレンツ変換 （ ローレンツ変換の逆変換 ） によって、 空間も時間も伸展します。」 と言うこともでき、 定説と異なる結論に達します。 定説では、 ローレンツ変換によって、 空間は伸展し時間は収縮し、 逆ローレンツ変換によって、 空間は収縮し時間は伸展します。 空間が収縮するというのは、 物質が短くなることを意味し、 時間が伸展するというのは、 物質の活動が遅くなることを意味します。

　 また、 の図 と の図 を比較してください。 物質Ｃ や 反物質Ｃ' の移動を表すベクトルは同じです。
　　　　 の 物質Ｃの移動を表すベクトルは、 直交座標系で、 次のように表されます。
　　　　　　　　　　
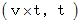
　　　　 の 物質Ｃの移動を表すベクトルは、 斜交座標系で、 次のように表されます。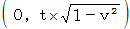
　　　　　　　　　　
　 と で物質Ｃの移動を表すベクトルが同じであるということは、 たとえば、 物質Ｃが移動中に１回転したという事実は、 と で共通であるということです。 したがって、 移動にかかる時間が よりも のほうが少ないので、 よりも のほうが回転スピードが速いことになります。

　 「 観察者によって物質の速さが異なるので、 観察者によって物質の長さや活動スピードが異なる。」 という相対性理論の定説に対して、 私は反論しています。 「 ローレンツ変換 」 は、 「 相対論的座標変換 」 ではなくて、 「 同一観察者の観察における、 ニュートン力学的観察 （ 第３者的な主観的観察 ） から 相対論的観察 （ 当事者的な客観的観察 ） への翻訳 」 なのだから、 「 観察者によって、 物質の長さが異なったり、 物質の活動のスピードが異なったり、 するようなことはない。」 というのが、 私見です。