(4) 今日の特殊相対性理論に対する批判
今日の特殊相対性理論では、 「 移動している慣性系は、 静止している慣性系に比べて、 時間が伸展し空間が運動方向に収縮している。 つまり、 移動している物質は状態変化のスピードが遅く、 移動している物質は運動方向に収縮している。」 というのが常識になっています。 定説はこれについての解説を次のような手段で行っています。
 物質が1自転する時間について、 当事者的な客観的観察 ( 物質が移動していないとみなされる慣性系で、 物質に対して静止している物さしを用いて観測する ) と 第3者的な主観的観察 ( 物質が移動しているとみなされる慣性系で、 観察者に対して静止している物さしを用いて観測する ) とを比べ、 その違いから 「 移動している慣性系では、 時間の経過スピードが遅い。」 と結論づける。
物質が1自転する時間について、 当事者的な客観的観察 ( 物質が移動していないとみなされる慣性系で、 物質に対して静止している物さしを用いて観測する ) と 第3者的な主観的観察 ( 物質が移動しているとみなされる慣性系で、 観察者に対して静止している物さしを用いて観測する ) とを比べ、 その違いから 「 移動している慣性系では、 時間の経過スピードが遅い。」 と結論づける。
 第3者的な主観的観察において同時刻に存在する2つの空点の距離について、 当事者的な客観的観察 と 第3者的な主観的観察 とを比べて、 その違いから 「 移動している慣性系の空間は運動方向に空間が収縮している 」 と結論づける。
第3者的な主観的観察において同時刻に存在する2つの空点の距離について、 当事者的な客観的観察 と 第3者的な主観的観察 とを比べて、 その違いから 「 移動している慣性系の空間は運動方向に空間が収縮している 」 と結論づける。
これは、 ローレンツ変換 あるいは 逆ローレンツ変換 の図で示すと次のようになります。
ただし、 物質 や 矢 の速さを  とします。
とします。
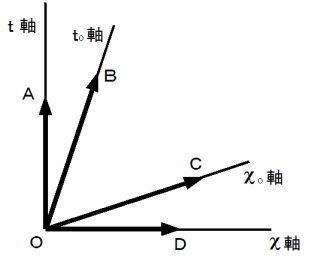
「 移動している物質の状態変化のスピードが遅こと 」 の解説は、 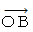 の直交座標系表示での時間の値が、 斜交座標系表示での時間の値よりも
の直交座標系表示での時間の値が、 斜交座標系表示での時間の値よりも  倍大きいことを示すことによって達成される。
倍大きいことを示すことによって達成される。
「 移動している物質が運動方向に収縮していること 」 の解説は、 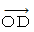 の直交座標系表示での空間の値が、 斜交座標系表示 での空間の値よりも小さくて
の直交座標系表示での空間の値が、 斜交座標系表示 での空間の値よりも小さくて 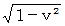 倍になっていることを示すことによって達成される。
倍になっていることを示すことによって達成される。
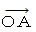 :
: 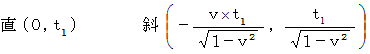
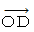 :
: 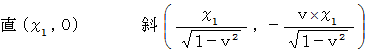
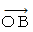 :
: 
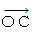 :
: 
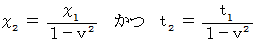 のときは、 直線AB は
のときは、 直線AB は 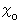 軸に平
軸に平行、 かつ、 直線CD は
 軸に平行 になり、 位置ベクトルはそれぞれ次の
軸に平行 になり、 位置ベクトルはそれぞれ次のようになる。
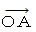 :
: 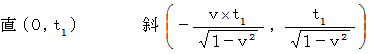
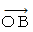 :
: 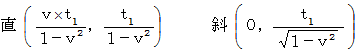
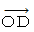 :
: 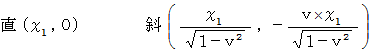
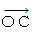 :
: 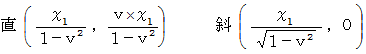
このように、 時空間位置ベクトルは、 その方向によって、 その空間値や時間値が、 斜交座標表示よりも直交座標表示の方が大きくなる場合もあるし小さくなる場合もあります。 したがって、 時空間位置ベクトルの選び方次第では、 移動している慣性系の時間や空間が収縮することもあり伸展することもあります。
では、 なぜ 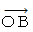 と
と 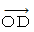 が選ばれたのでしょうか?
が選ばれたのでしょうか? 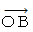 と
と 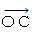 や
や 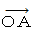 と
と 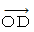 のように対称的になっていないのに不自然さを感じるのは私だけでしょうか?
のように対称的になっていないのに不自然さを感じるのは私だけでしょうか?
それは、 次の理由によります。 静止している矢の長さを計るのであれば、 異なる時刻に矢の両端が存在する空点を観察してもいいのですが、 移動している矢の長さを計るためには、同時刻に矢の両端が存在する空点を観察しなければなりません。 それには写真を撮って時間を止めた状態にしてから観察するといいかもしれませんが、 物理学的観察は認識とは違いますので、 写真をとらなくてもきちんと観察できるものとします。 直線座標系では矢は移動しており、斜交座標系では矢は静止しています。 したがって、 直線座標系では同時刻に矢の両端が存在する空点を観察しなければなりませんが、 斜交座標系では同時刻に矢の両端が存在する空点を観察しなくともその長さを測ることができます。 したがって、 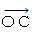 でなくて
でなくて 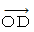 なのです。
なのです。
では、 点状物質が1回転する時間を計るのには、 点状物質はずっと同じ空点に存在しなくていいのでしょうか? 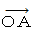 でなくて
でなくて 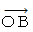 でいいのでしょうか? 点状物質が1回転する時間を計るのには、 点状物質が1回転し始める時点と1回転し終わる時点とを観察する必要があります。 そのためには時間の流れを待たなければなりません。 私たちは空間については一時点にして無限大に観察 ( 認識ではありません ) することができますが、 時間については一空点にして一時点しか観察することができないのです。 ちょっと話が横道にそれてしまいましたが、 答えは 「
でいいのでしょうか? 点状物質が1回転する時間を計るのには、 点状物質が1回転し始める時点と1回転し終わる時点とを観察する必要があります。 そのためには時間の流れを待たなければなりません。 私たちは空間については一時点にして無限大に観察 ( 認識ではありません ) することができますが、 時間については一空点にして一時点しか観察することができないのです。 ちょっと話が横道にそれてしまいましたが、 答えは 「 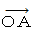 でなくて
でなくて 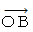 でいいのだ。」 です。 なぜなら、 第3者的な客観的観察 ( ニュートン力学的観察 ) においては、 同一の慣性系内であれば、 すべての空点で時刻は同一になっているからです。 では、 時間経過のスピードを比較するために
でいいのだ。」 です。 なぜなら、 第3者的な客観的観察 ( ニュートン力学的観察 ) においては、 同一の慣性系内であれば、 すべての空点で時刻は同一になっているからです。 では、 時間経過のスピードを比較するために 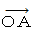 でなくてわざわざ
でなくてわざわざ 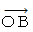 を選択する理由は何でしょうか? 当事者的な客観的観察 ( 相対論的観察 ) においては、 同一の慣性系内であっても、 空点が異なると時刻が異なるからでしょうか? いいえ、 そんなことはありません。 では何故でしょうか? それは、 相対性理論には 「 座標変換にて固有時間は不変である。」 という定理があり、 それを過剰に意識しているためであると考えます。 固有時間とは、 当事者的な客観的観察における時間です。 固有時間は、 当事者的な客観的観察 ( 斜交座標系 ) の時間なのですが、 これを 「 静止している物質に宿る物質固有の時間 」 であると勘違いしているから、
を選択する理由は何でしょうか? 当事者的な客観的観察 ( 相対論的観察 ) においては、 同一の慣性系内であっても、 空点が異なると時刻が異なるからでしょうか? いいえ、 そんなことはありません。 では何故でしょうか? それは、 相対性理論には 「 座標変換にて固有時間は不変である。」 という定理があり、 それを過剰に意識しているためであると考えます。 固有時間とは、 当事者的な客観的観察における時間です。 固有時間は、 当事者的な客観的観察 ( 斜交座標系 ) の時間なのですが、 これを 「 静止している物質に宿る物質固有の時間 」 であると勘違いしているから、 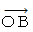 でなくてはだめだと考えてしまうのだろうと思います。
でなくてはだめだと考えてしまうのだろうと思います。
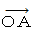 を選んでいたとしたら、 移動している物質の状態変化のスピードは速いことになったはずです。
を選んでいたとしたら、 移動している物質の状態変化のスピードは速いことになったはずです。このように、 時空間位置ベクトルは、 その方向によって、 その空間値や時間値が、 斜交座標表示よりも直交座標表示の方が大きくなる場合もあるし小さくなる場合もあります。 しかし、 これでいいのです。 それなのに
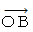 と
と 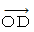 のみをピックアップして、 それから得られる 「 ニュートン力学的観察 」 と 「 相対論的観察 」 の違いを、 移動している慣性系と静止している慣性系での、 時間経過スピードの違いや空間の体積の違いにすり変えているのが、 今日の特殊相対性理論であると、 私は考えています。
のみをピックアップして、 それから得られる 「 ニュートン力学的観察 」 と 「 相対論的観察 」 の違いを、 移動している慣性系と静止している慣性系での、 時間経過スピードの違いや空間の体積の違いにすり変えているのが、 今日の特殊相対性理論であると、 私は考えています。
 次のページへ進む
次のページへ進む