(5) ニュートン力学的観察 と 相対論的観察 を結ぶ 固有時間不変の定理
ニュートン力学的観察 と 相対論的観察とでは、 「 AのBに対する速さ 」 が違います。 例えば、 相対論的観察 ( 斜交座標系 ) では、 「 光速不変の原理 」 により、 速さ  で移動しているA君に対するA君に真正面から向かって来る光の速さは
で移動しているA君に対するA君に真正面から向かって来る光の速さは  ですが、ニュートン力学的観察 ( 直交座標系 ) では、 A君に対するA君に真正面から向かって来る光の速さは
ですが、ニュートン力学的観察 ( 直交座標系 ) では、 A君に対するA君に真正面から向かって来る光の速さは 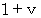 です。
です。
これに対して、 ニュートン力学的観察 と 相対論的観察 とでは、 「 固有時間 」 は必ず等しくなっています。 例えば、 ニュートン力学的観察において 「 フィギュアスケーターが1秒間に3回転して2m移動した。」 は、 フィギュアスケーターの立場で観察する相対論的観察に翻訳すると、 「 フィギュアスケーターが同じ位置で1秒間よりも短い時間に3回転した。」 になります。 ( 相対論的観察は、 物質に起こった出来事の時刻については、 物質が移動していないとみなして観察します。) このように、 ニュートン力学的観察 と 相対論的観察とでは、 フィギュアスケーターが3回転する間の経過時間と移動空間が異なります。 しかし、 固有時間は同一です。 式で表すと次のようになります。
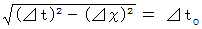
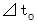 が、 相対論的観察による時間で、 固有時間になります。
が、 相対論的観察による時間で、 固有時間になります。
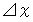 はニュートン力学的観察による移動空間で、
はニュートン力学的観察による移動空間で、 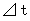 はニュートン力学的観察による時間です。
はニュートン力学的観察による時間です。
この 「 固有時間不変の定理 」 は 「 光速不変の原理 」 に由来します。 ニュートン力学的観察において 「 静止している観察者Aに対する光子の速さは  であり、 運動している観察者Bに対する光子の速さは
であり、 運動している観察者Bに対する光子の速さは  ではない。」 ですが、 これを観察者Aによる観察者Bの立場に立った相対論的観察に翻訳すると、 「 光速不変の原理 」 に由り、 「 観察者Bに対する光子の速さは
ではない。」 ですが、 これを観察者Aによる観察者Bの立場に立った相対論的観察に翻訳すると、 「 光速不変の原理 」 に由り、 「 観察者Bに対する光子の速さは  である。」 となります。 これは 「 2人の相対的等速直線運動をしている観察者たちがいるとき、 静止しているとみなされる2人の観察者に対する同一の光子の速さ 」 は同一であるということです。 これに対して、 一般の物質の移動について言うと、 ニュートン力学的観察において 「 静止している観察者Aに対する物質Cの速さは
である。」 となります。 これは 「 2人の相対的等速直線運動をしている観察者たちがいるとき、 静止しているとみなされる2人の観察者に対する同一の光子の速さ 」 は同一であるということです。 これに対して、 一般の物質の移動について言うと、 ニュートン力学的観察において 「 静止している観察者Aに対する物質Cの速さは  であり、 運動している観察者Bに対する物質Cの速さは
であり、 運動している観察者Bに対する物質Cの速さは  ではない。」 が、観察者Aによる観察者Bの立場に立った相対論的観察に翻訳されると、 「 静止している観察者Bに対する物質Cの速さは
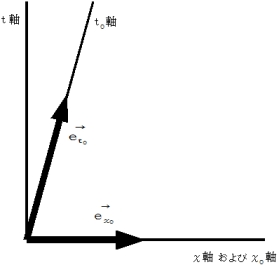
ではない。」 が、観察者Aによる観察者Bの立場に立った相対論的観察に翻訳されると、 「 静止している観察者Bに対する物質Cの速さは  ではない。」 となり、 「 2人の相対的等速直線運動をしている観察者たちがいるとき、 静止しているとみなされる2人の観察者に対する同一の物質の速さ 」 は異なります。 したがって、 光子の速さは一般の物質の速さとは違う特別なものです。 よって、 光子の移動と物質の移動を同一線上のものと捉えるわけにはいけません。 しかし、 「 2人の相対的等速直線運動をしている観察者たちがいるとき、 静止しているとみなされる2人の観察者に対する同一の光子の速さ 」 のように、 2人の観察者にとって共通するものであって、 なおかつ、 それが光子の移動と物質の移動に関して2人の観察者にとって共通する他の何かを持っていれば、 光子の移動と物質の移動を同一線上のものと捉えることができるはずです。 そこで、 まず、 光子の移動に関して、2人の観察者に共通するものを探してみましょう。 そのために、 1つのベクトルで表される光子の移動について、 直交座標系表示 ( ニュートン力学的観察 ) と 斜交座標表示 ( 相対論的観察 ) とを比べてみます。 すると、 ありますあります、 共通するものが。
ではない。」 となり、 「 2人の相対的等速直線運動をしている観察者たちがいるとき、 静止しているとみなされる2人の観察者に対する同一の物質の速さ 」 は異なります。 したがって、 光子の速さは一般の物質の速さとは違う特別なものです。 よって、 光子の移動と物質の移動を同一線上のものと捉えるわけにはいけません。 しかし、 「 2人の相対的等速直線運動をしている観察者たちがいるとき、 静止しているとみなされる2人の観察者に対する同一の光子の速さ 」 のように、 2人の観察者にとって共通するものであって、 なおかつ、 それが光子の移動と物質の移動に関して2人の観察者にとって共通する他の何かを持っていれば、 光子の移動と物質の移動を同一線上のものと捉えることができるはずです。 そこで、 まず、 光子の移動に関して、2人の観察者に共通するものを探してみましょう。 そのために、 1つのベクトルで表される光子の移動について、 直交座標系表示 ( ニュートン力学的観察 ) と 斜交座標表示 ( 相対論的観察 ) とを比べてみます。 すると、 ありますあります、 共通するものが。
それは、 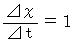 と
と 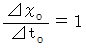 という式の形式です。
という式の形式です。
これらの式より、 光子の移動については、 次の式が成り立っていますので、
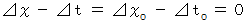
物質の移動については、 次の式が成り立つと仮定します。
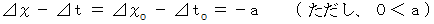
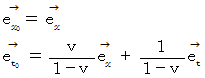
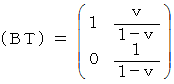
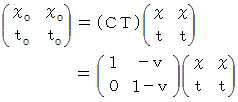
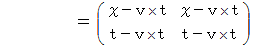

すると、 速さ
 で移動している物質については、 ニュートン力学的観察 と 相対論的観察 では、 空間の幅は同じですが、 時間については、 ニュートン力学的観察のほうが 相対論的観察よりも
で移動している物質については、 ニュートン力学的観察 と 相対論的観察 では、 空間の幅は同じですが、 時間については、 ニュートン力学的観察のほうが 相対論的観察よりも 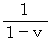 倍 長くなります。 これは、 今日の相対論的に言うと、 「 移動している物質の活動スピードは
倍 長くなります。 これは、 今日の相対論的に言うと、 「 移動している物質の活動スピードは 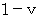 倍 になり、 静止しているときよりも遅くなる。」 ということになります。 今日の相対性理論とは異なります。
倍 になり、 静止しているときよりも遅くなる。」 ということになります。 今日の相対性理論とは異なります。では、 どうして、 この式は採用されず、 代わりに
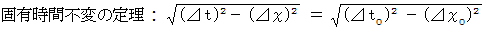 を持っているローレンツ変換にその席を譲ったのでしょうか? それは、 電磁気学の基本方程式であるマクスウェルの方程式について、 相対性原理 ( 物理学法則はどんな座標系でも成立するという原理 ) が守られるための座標変換が、 ローレンツ変換であったためです。 ローレンツ変換は、 物質の移動についても光の移動と共通する次の式が成立していると仮定しています。
を持っているローレンツ変換にその席を譲ったのでしょうか? それは、 電磁気学の基本方程式であるマクスウェルの方程式について、 相対性原理 ( 物理学法則はどんな座標系でも成立するという原理 ) が守られるための座標変換が、 ローレンツ変換であったためです。 ローレンツ変換は、 物質の移動についても光の移動と共通する次の式が成立していると仮定しています。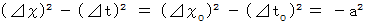
*
 は 固有時間です。
は 固有時間です。光の場合は、

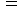
 です。
です。この式を証明する実験は困難であり、 未だにこの仮定が正しいのか間違いなのか証明されていないと、 私は考えています。
 次のページへ進む
次のページへ進む