(1) 暗号の進化
-
昔は、 暗号化とその解読は、 関数と逆関数の原理を使用していました。 ある文章を暗号化して公開し、 それを仲間が解読するためには、 仲間と自分に共通する 関数 と その逆関数 と 暗証番号 の3つがあればよかったのです。 文字はコード表によって数値に置き換えることができますので、 文章の暗号化とは数値の暗号化に他なりません。 そのモデルを十進BASIC を使ってプロブラミングしてみました。 コンピューターのプログラムとは、 関数の一種です。
A → □ → A’ → ■ → A
 四角は関数です。
四角は関数です。でも、 この方法はあまりも常識すぎて、 すぐに他人から解読されてしまいそうです。 そこで、 進んだ距離だけ後戻りするのではなく、 さらに先に一定の距離だけ進めることによって元に戻そうという発想が生まれてきたのです。 それには周期関数を利用します。 どれだけ先に進めると元に戻るのかは、 周期関数が持っている周期によって異なりますので、 元の数値がどれだけ進められて変換されているのかが解かったとしても、 元に戻す方法が解らないのです。
中には周期が自明な周期関数もあります。 たとえば、 回転という座標変換であれば、 120度回転させたものならば、 さらに240度回転させれば元に戻ることが解るのですが、 それは回転という座標変換の周期が360度であることを私たちは知っているからです。 ですから、 回転による点の暗号化はすぐに他人から解読されてしまう恐れがあります。 それはともあれ、 周期関数を利用した暗号化の例として、 回転による点の暗号化と解読法について見ていきましょう。
たとえば、
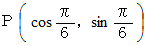 が真実の点であるとします。 これを暗号化して P’にします。 たとえば、 反時計回りに60度回転させて得られる P’( 0 , 1 ) です。 それは次のようにして求めます。
が真実の点であるとします。 これを暗号化して P’にします。 たとえば、 反時計回りに60度回転させて得られる P’( 0 , 1 ) です。 それは次のようにして求めます。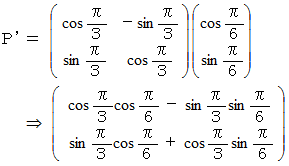
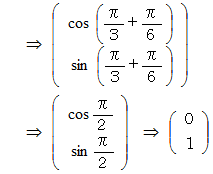
そこでヒントとして
 を公開しておきます。 回転においては、 周期が2πであることは自明のことですので、 解読は次のようになります。
を公開しておきます。 回転においては、 周期が2πであることは自明のことですので、 解読は次のようになります。
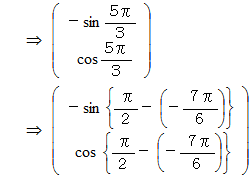
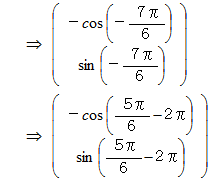

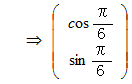
なお、 逆関数を使う解読法は次のようになります。

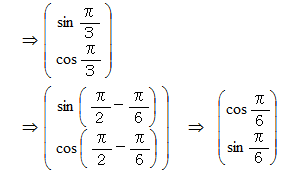
-
RSA 暗号 は、 周期関数を利用したものです。 暗号化するのにどれだけ進めたのかを公表しますが、 周期を公表しませんので、 周期がわかる暗証番号を知っている人でなければ解読できません。
自然数 mh を自然数 n で割った余りは、h = 1 から1ずつ増やしていくと、どこかで h = 1 のときと等しくなります。さらに h を1ずつ増やしていきそれをずっと続けると、ある周期 u を持って h = 1 のときと等しくなります。
自然数値化された文字が m に相当します。自然数値化された文字を暗号化するには、m を w ( ただし、w は 1 より大きくて u より小さい u の約数で素数 ) 乗したものを n で割った余りの数に置き換えます。 自然数値化された文字を見つけるには、暗号化された数を u/w 乗したものを n で割った余りを求めます。
-
A, b, c, n, m, P を自然数、 S, T, j, k を素数とします。
A は 自然数値化された文字に相当します。 S と T は 暗号でやりとりする2人だけが知っている素数です。 k も 暗号でやりとりする2人だけが知っています。
n = S × T であり、「 n は割る数ですよ」と暗号を解くヒントとして公表します。 また、j も「これは暗号化するときに用いた累乗数ですよ」と暗号を解くヒントとして公表します。
暗号をやりとりする2人のうち暗号を受け取る方が、もし S か T のどちらかを忘れてしまったとしても、n が公表されるので、k さえ覚えておけば暗号を解くことが出来ます。
n が大きな数のとき、 n = S × T という形に素因数分解することは相当に困難です。 例えば「 1694952641 を素因数分解すると S × T の形になるが、 S と T の数字を求めよ。」という問題があるときに、 コンピューターでも答えにたどり着くまでに相当な時間がかかります。 答えは 3323 × 510067 なのですが。 RSA 暗号 では、 実際に S と T の数字が解れば、 たとえ k の値を知らなくとも、あとどれだけ進めれば元に戻るのかが解るのですが、 S と T の数字を発見するのが至難の業なのです。
MOD( A ,n )は A を n で割った余りを表します。
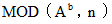 を 「 A についての n を法とし b を累乗数とする 累乗剰余数 」 と言うことにします。
を 「 A についての n を法とし b を累乗数とする 累乗剰余数 」 と言うことにします。n = S × T のとき、「 ある自然数についての n を法とし b を累乗数とする 累乗剰余数 がその自然数に等しくなる。」ということが、 n 未満の全て自然数で生じることがあり、そのときの累乗数 b は、 次のように表されます。
 ・ ・ ・( 重要な性質その1 )
・ ・ ・( 重要な性質その1 )( m = 1,2,3,4,・・・ )
※ 参考: 数理論 > 乗余数の性質 の(8)(9)
※ 参考: 数理論 > オイラーの定理
たとえば、 「 ある自然数についての 253 を法とし b を累乗数とする 累乗剰余数 がその自然数に等しくなる。」 ということが、 253 = 11 × 23 未満の全ての自然数で生じているときの累乗数 b は、 小さい順に次のようになります。
111 221 331 441 551 661 ・ ・ ・ ・
これは、 累乗数に関して周期 110 でそういうことが生じるということです。
ここで、
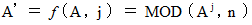 ( A < n ) という関数を考えます。
( A < n ) という関数を考えます。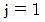 のとき
のとき 
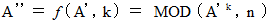 とすると、
とすると、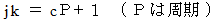 のとき、
のとき、 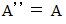 ・ ・ ・( 重要な性質その2 )
・ ・ ・( 重要な性質その2 )※ 参考: 数理論 > 乗余数の性質 の(9)
たとえば、 累乗数 b : 111 221 331 441 551 661 ・ ・ ・ ・ のとき、
これらの数のうち j k と表現することのできる数を探しますと、 111 = 3 × 37 があります。
すると次のようになります。
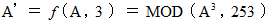
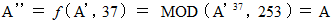
このことを確かめるためのプログラムを3つ、 十進BASIC で作ってみました。
-
I love you. → キャラクターコードによる数列化
→ 73 32 108 111 118 101 32 121 111 117 46
公開鍵 : ( 累乗数 3 , 法 253 )
秘密鍵 : ( 累乗数 37 )
暗号化は、 数列の数たちを 「 それぞれの数についての 253 を法とし 3 を累乗数とする 累乗剰余数 」 に置き換えるという操作になります。 公開鍵の情報によってここまではみんなすぐに分かるのですが、 これを元に戻す方法は、 秘密鍵の情報がない限り簡単に見つかりません、
解読は、 暗号化数列の数たちを「 それぞれの数についての 253 を法とし、 37 を累乗数とする 累乗剰余数 」に置き換えるという操作になります。 そして、 得られた数列をキャラクターコード表によって文字に変換しますと、 I love you. になります。
もし、秘密鍵を知らない人が暗号を解読しようとすると、まず、253 が 11 × 23 で表されることを見つけなければなりません。そして次に 10 と 22 の最小公倍数が 110 であることを見つけなければなりません。それから、110+1 が 3 × 37 で表されることを見つけなければなりません。
このケースについて、 暗号化および解読のプログラムを十進BASIC で作ってみました。
-
公開鍵は、暗号を解読するためのヒントに相当します。 暗号化された数は自然数値化された文字を何乗かしたものをある数で割った余りなのですが、何乗していてどんな数で割っているのかをヒントとして公開するのです。 秘密鍵は、暗号化された数を何乗してから公開鍵で示された数で割った余りを求めればいいのかを示すものです。
公開鍵: 法 と 暗号化のための累乗数 ※ 法 = 割る数 = 素数S × 素数T
秘密鍵: 解読のための累乗数
秘密鍵の数を見つけるには、公開鍵で示された割る数を素因数分解して、2つの約数となる素数を見つけて( 相当に困難です )から、それらから 1 引いた数どうしの最小公倍数を見つけて、それに 1 を足したものを公開鍵で示された累乗数で割ります。
公開鍵の累乗数: (S−1) や (T−1) と互いに素な数( j とする )
秘密鍵の累乗数: k とする
(S−1) と (T−1) の最小公倍数 を W とする。 ← オイラーの定理に由来
jk − 1 = mW ( m は 任意の自然数 ) が成り立つ。
自然数値化された文字 A の暗号化: MOD ( Aj, 法 )
MOD ( Aj, 法 ) の解読:
MOD ( {MOD ( Aj, 法 ) }k, 法 ) = ( Ajk (mod 法) =→ Ajk (mod 法)
=→ Ajk−1 × A (mod 法) =→ AmW × A (mod 法) =→ 1 × A (mod 法)
=→ A (mod 法)
 数理論 へ戻る
数理論 へ戻る