（１）　回転中心を同定する方法

　 正方形の折り紙を２枚用意してください。 この２枚を少しずらせて重ね合わせます。 そのときに影をみると１６角形の星型になるようにします。 では、 上の正方形だけを 平行移動 または 回転 させて２枚の折り紙をきちんと重ねて合わせてください。

　 すると、 まず上の正方形の重心を回転中心として正方形の辺がそれぞれ平行になるように回転させてから、 きちんと重なるように上の正方形を平行移動させる人と、 まずどれかの頂点が重なるように上の正方形を平行移動させてから、 その重なった頂点を回転中心として上の正方形を回転させる人とに分かれると思います。 あなたはどっちですか？

　 では、 平行移動せずに回転だけで２枚の折り紙をきちんと重ねて合わせてくださいと言われたらできますか？　その回転の中心点Ｐは不動点と言われます。

不動点の証明 ：

∠ＡＥＣ ＝ ∠ＥＣＤ ＝ ９０°
∠ＢＦＣ ＝ ∠ＦＣＡ ＝ ９０°
ＥＣ ＝ ＦＣ
∠ＣＡＢ ＝ χ°
∠ＥｅＰ ＝ ∠ＦｆＰ ＝ ９０°



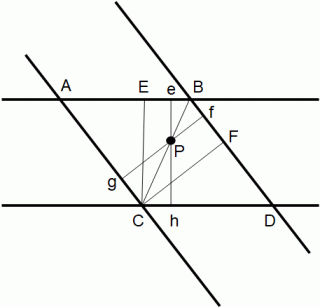
△ＡＥＣ と △ＤＦＣ は相似
△ＢＥＣ と △ＢｅＰ は相似
△ＢＦＣ と △ＢｆＰ は相似
∠ＥＣＦ ＝ ∠ｅＰｆ ＝ ∠ｈＰｇ ＝ χ°
ｅＰ ＝ ｆＰ
ｈＰ ＝ ｇＰ

　 点Ｃを中心に、 直線ＡＣと直線ＢＤを反時計回りにχ°回転すると、 それぞれ、 直線ＣＤと直線ＡＢに重なる。
　 線分ＢＣ上の点Ｐを中心に、 直線ＡＣと直線ＢＤを反時計回りにχ°回転すると、 それぞれ、直線ＣＤと直線ＡＢに重なる。