(3) 社会的総資本の増大方程式
-
先ほどの式6つを再掲します。
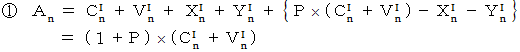
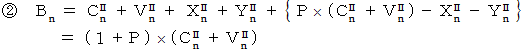
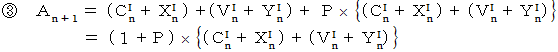
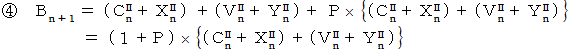
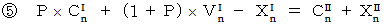

 グループにおける、 投下資本金に占める材料や道具の費用の比率を
グループにおける、 投下資本金に占める材料や道具の費用の比率を 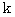 とし、
とし、  グループにおける、 投下資本金に占める材料や道具の費用の比率を
グループにおける、 投下資本金に占める材料や道具の費用の比率を  とし、
とし、 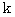 や
や  は時間的に一定であると仮定します。 すると、 次のようになります。
は時間的に一定であると仮定します。 すると、 次のようになります。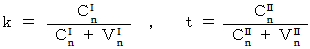

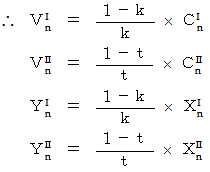
すると、

 は次のようになります。
は次のようになります。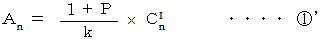
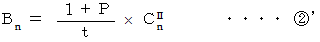
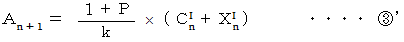
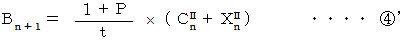
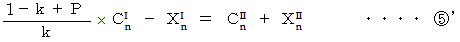
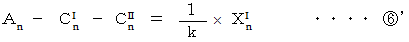
 より、
より、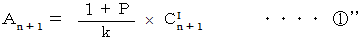
 より、
より、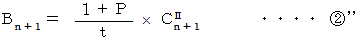
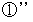 と
と 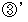 より、
より、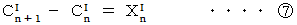
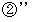 と
と  より、
より、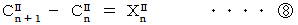
 と
と  より、
より、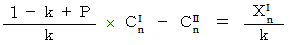
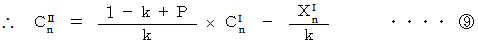
 と
と 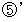 より、
より、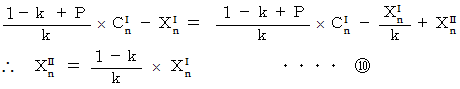
 と
と  より、
より、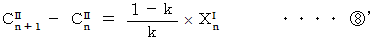
 より、
より、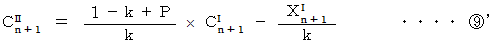
 と
と  より、
より、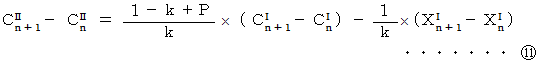
 と
と  と
と  より、
より、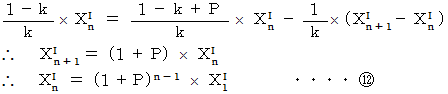
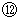 と
と  より、
より、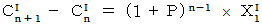
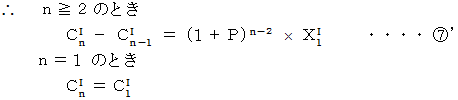
 と
と  より、
より、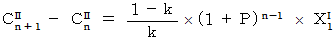
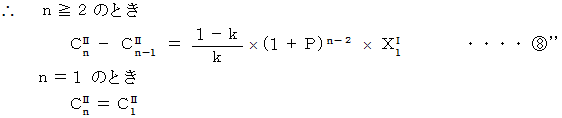
 より、
より、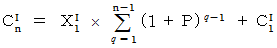
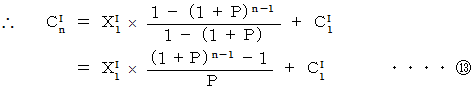
同様にして、
 より、
より、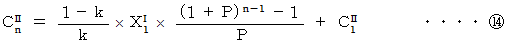
 と
と  より、
より、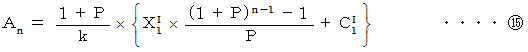
 と
と  より、
より、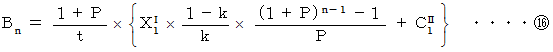
 ただし、
ただし、
 は、 平均利潤率である。
は、 平均利潤率である。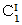 は、
は、  グループ における、 初回の資本の回転時に投与された
グループ における、 初回の資本の回転時に投与された材料や道具の費用であり、
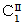 は、
は、  グループ における、 初回の
グループ における、 初回の資本の回転時に投与された材料や道具の費用である。
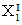 は、
は、 
グループにおける<第2回目の資本の回転の時、 拡大再生産ぶんと
して組み入れられる部分の内の、 材料や道具の費用になるぶんで
ある。
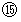 と
と 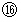 が、 理想的な経済モデルでの社会的総資本の増大方程式です。 単利ローンのような
が、 理想的な経済モデルでの社会的総資本の増大方程式です。 単利ローンのような  倍の式ではなく、 複利ローンのような
倍の式ではなく、 複利ローンのような  乗の式になっていることに注目してください。 つまり、 社会の富は、 雪だるま式に大きくなっていきます。 もちろん、 次第に
乗の式になっていることに注目してください。 つまり、 社会の富は、 雪だるま式に大きくなっていきます。 もちろん、 次第に 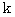 や
や  は増大していくので、 こんなに簡単な式ではすみません。 その上、 このモデルは、 国内での非商品経済部分の商品経済への転換の余地のある場合のモデルですから、 このような式になっているのです。 したがって、 この式は現在ではほとんど使用価値はありません。
は増大していくので、 こんなに簡単な式ではすみません。 その上、 このモデルは、 国内での非商品経済部分の商品経済への転換の余地のある場合のモデルですから、 このような式になっているのです。 したがって、 この式は現在ではほとんど使用価値はありません。 次ページへ進む
次ページへ進む