（４） 複合命題の真偽
-
「 私は子である。」という命題が真の場合について考えます。 このとき、「 私は親である。」という命題は、 人によっては真の場合も偽の場合もあります。 したがって、「 私は子であるか、 または、 私は親である。」という命題は、 どの人にとっても真になり、「 私は子であり、 かつ、 私は親である。」という命題は、 ある人にとっては偽になります。 このような「 合成命題 」のことを、 私は「 複合命題 」と言っています。「 複合命題 」にも真偽があります。「 または 」の入った複合命題の場合は、「 私は子である。」という命題が真であるか、 または、「 私は親である。」という命題が真であるならば、 真になりますが、「 かつ 」の入った複合命題の場合は、「 私は子である。」という命題が真であり、 かつ、「 私は親である。」という命題が真でなければ、 真になりません。
複合命題の真偽の判定には、 集合論でよく使われるベン図が便利です。
「 私は子である。」という命題をＡとし、「 私は親である。」という命題をＢとします。
命題Ａが真のときを、 次のように表すことにします。
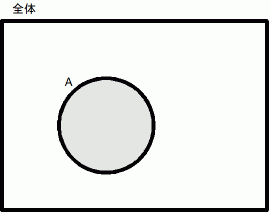
命題Ａが偽のときを、 次のように表すことにします。
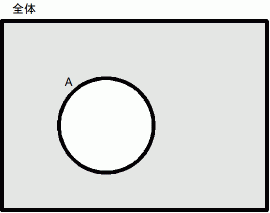
例えば、 命題Ａが偽で命題Ｂが真のときは、 次のように図を重ねます。
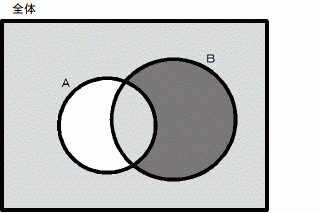
また、 命題Ａが偽で命題Ｂも偽のときは、 次のように図を重ねます。
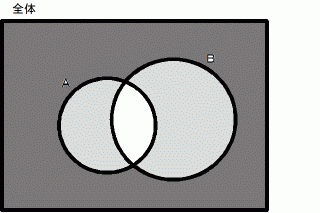
このように重ねた図のサークルＡとサークルＢが共有する （ 重なる ） 部分の色を見てください。「 または 」の入った複合命題の場合は、 そこが白のときは偽で、 それ以外は真になります。「 かつ 」の入った複合命題の場合は、 そこが濃いグレイのときは真で、 それ以外は偽になります。
-
「 吾輩は猫である。」という命題が「 真 」であるならば、「 吾輩は動物である。」という命題は必ず「 真 」になります。 それは「 猫 」という集合が「 動物 」という集合に内包されているからです。「 もし吾輩が猫であるのならば、 吾輩は動物である。」というのも命題であり、 このような「 合成命題 」のことを「 包含命題 」と私は言っています。「 ならば 」の前に来る部分命題は「 前件 」と言い、「 ならば 」の後にくる部分命題は「 後件 」と言います。
-
前 件
後 件
前件
後件真
真
真（誠真）
真
偽
偽（誠偽）
偽
真
真
偽
偽
真
-
前 件
後 件
前件
後件真
真
真
真
偽
真
偽
真
偽（誠偽）
偽
偽
真（誠真）
-
前 件
後 件
前件
後件真
真
真
真
偽
偽
偽
真
偽
偽
偽
偽
-
前 件
後 件
前件
後件真
真
偽
真
偽
偽
偽
真
偽
偽
偽
真
「 もし 」の入った包含命題は、「 吾輩は猫である。」という命題が真であり、 かつ、「 吾輩は動物である。」という命題が偽であるならば、 偽になりますが、 その他の場合は、 すべて真になります。 また、 この命題の「 前件 」と「 後件 」を置き換えた「 集合の逆包含関係 」が成り立っている場合の「 包含命題 」（ 具体的には「 もし吾輩が動物であるのならば、 吾輩は猫である。」という命題になります。） については、「 吾輩は動物である。」という命題が偽であり、 かつ、「 吾輩は猫である。」という命題が真であるならば、 偽になりますが、 その他の場合は、 すべて真になります。
順包含関係の場合の 包含命題の真偽表
逆包含関係の場合の 包含命題の真偽表
表で、（ 誠真 ）や（ 誠偽 ）と書いたところは、 納得できると思いますが、 それ以外のところは、「 反対じゃないの？」と思われる人が多いと思います。 この表は「 疑わしきは罰せず 」の立場をとる哲学の世界での判定だからなのです。
ケースバイケースの場合は、 次のようになっています。
現実の世界 ： ケースバイケースで、 真もあり偽もあり
数学の世界 ： 偽とする
哲学の世界 ： 真とする
実は、 哲学の世界における包含命題の真偽の判定方法は、 次のような手順になっているのです。
「私は子である。」
真か偽か？ 証言 ： ○ です。「私は親である。」
真か偽か？ 証言 ： □ です。この２つの証言から、 包含命題が偽であることが証明できるのなら、 この包含命題は偽であり、 証明できないのなら、 この包含命題は真である。 なお、「 包含命題が偽であることの証明 」とは「 すべての主語の場合において、 包含命題が偽になることを明らかにするということ。」である。
では、 一つずつ見ていくことにしましょう。
「 吾輩は猫である。」
真か偽か？ 証言 ： 真です。「 吾輩は動物である。」
真か偽か？ 証言 ： 真です。この２つの証言から、「 吾輩は猫であるので、 吾輩は動物である。」は真である。
したがって、 この２つの証言から「もし吾輩が猫であるのならば、 吾輩は動物である。」が偽であることが証明できないので、 この包含命題は真である。
これをベン図で書くと、 次のようになります。
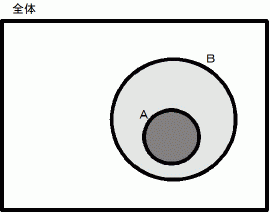
「 吾輩は猫である。」
真か偽か？ 証言 ： 真です。「 吾輩は動物である。」
真か偽か？ 証言 ： 偽です。この２つの証言から、「 吾輩は猫であるので、 吾輩は動物ではない。」は偽である。
したがって、 この２つの証言から「 もし吾輩が猫であるのならば、 吾輩は動物である。」が偽であることが証明できるので、 この包含命題は偽である。
これをベン図で書くと、 次のようになります。
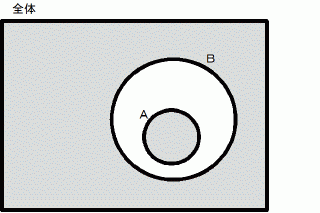
「 吾輩は猫である。」
真か偽か？ 証言 ： 偽です。「 吾輩は動物である。」
真か偽か？ 証言 ： 真です。この２つの証言から、「吾輩は猫ではないので、 吾輩は動物である。」は、 吾輩が米の場合は偽になるが、 吾輩が犬の場合は真になる。
したがって、 この２つの証言から「 もし吾輩が猫であるのならば、 吾輩は動物である。」が偽であることが証明できないので、 この包含命題は真である。
これをベン図で書くと、 次のようになります。
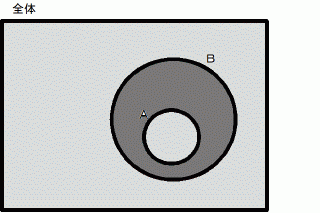
「 吾輩は猫である。」
真か偽か？ 証言 ： 偽です。「 吾輩は動物である。」
真か偽か？ 証言 ： 偽です。この２つの証言から、「 吾輩は猫ではないので、 吾輩は動物ではない。」は、 吾輩が犬の場合は偽になるが、 吾輩が米の場合は真になる。
したがって、 この２つの証言から「 もし吾輩が猫であるのならば、 吾輩は動物である。」が偽であることが証明できないので、 この包含命題は真である。
これをベン図で書くと、 次のようになります。
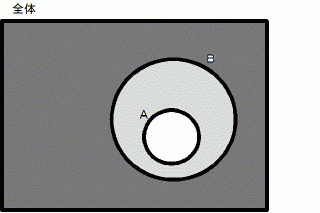
（ ここからは、 逆包含関係です。）
「 吾輩は動物である。」
真か偽か？ 証言 ： 真です。「 吾輩は猫である。」
真か偽か？ 証言 ： 真です。この２つの証言から、「 吾輩は動物であるので、 吾輩は猫である。」は、 吾輩が猫の場合は真であるが、 吾輩が犬の場合は偽である。
したがって、 この２つの証言から、「 もし吾輩が動物であるのならば、 吾輩は猫である。」が偽であることが証明できないので、 この包含命題は真である。
これをベン図で書くと、 次のようになります。
「 吾輩は動物である。」
真か偽か？ 証言 ： 真です。「吾輩は猫である。」
真か偽か？ 証言 ： 偽です。この２つの証言から、「 吾輩は動物であるので、 吾輩は猫ではない。」は、 吾輩が犬の場合は真であるが、 吾輩が猫の場合は偽である。
したがって、 この２つの証言から「 もし吾輩が動物であるのならば、 吾輩は猫である。」が偽であることが証明できないので、 この包含命題は真である。
これをベン図で書くと、 次のようになります。
「 吾輩は動物である。」
真か偽か？ 証言 ： 偽です。「 吾輩は猫である。」
真か偽か？ 証言 ： 真です。この２つの証言から、「 吾輩は動物ではないので、 吾輩は猫である。」は偽である。
したがって、 この２つの証言から「 もし吾輩が動物であるのならば、 吾輩は猫である。」が偽であることが証明できるので、 この包含命題は偽である。
これをベン図で書くと、 次のようになります。
「 吾輩は動物である。」
真か偽か？ 証言 ： 偽です。「 吾輩は猫である。」
真か偽か？ 証言 ： 偽です。この２つの証言から、「 吾輩は動物でないので、 吾輩は猫ではない。」は真である。
したがって、 この２つの証言から、「 もし吾輩が動物であるのならば、 吾輩は猫である。」が偽であることが証明できないので、 この包含命題は真である。
これをベン図で書くと、 次のようになります。
これらの重ね合わせたベン図からわかることは、 どこかに濃いグレイがある場合は、 その包含命題は真であり、 どこにも濃いグレイがない場合は、 その包含命題は偽であることがわかります。
今までは、 哲学の世界における包含命題の真偽について述べましたが、 数学の世界における包含命題の真偽はそれと異なります。
数学の世界での 順包含関係の場合の 包含命題の真偽表
包含命題が真になるのは、 次のベン図のときのみです。数学の世界での 逆包含関係の場合の 包含命題の真偽表
包含命題が真になるのは、 次のベン図のときのみです。つまり、 前件のグレイの範囲が、 後件のグレイの範囲に完全に含まれているときのみが、 数学の世界では「 真」の包含命題になります。 数学では、 すべてのケースについて包含命題の文章が正しくない限り、 その包含命題は真ではないのです。
次のページへ進む