(6) 包含命題の「 逆 」「 裏 」「 対偶 」
-
さて、 包含命題には、「 逆 」「 裏 」「 対偶 」があります。「 逆 」は、「 集合の順包含関係 」が成り立っているときの包含命題 と「 集合の逆包含関係 」が成り立っている場合の包含命題との関係であり、 今見てきたところです。「 逆 」も含めて、「 裏 」と「 対偶 」について具体的に見てみましょう。
基本包含命題の例 : ( このケースでは、 順包含関係になっている。)
「 もし吾輩が猫であるならば、 吾輩は動物である。」
( 真なので真は
 誠真 )
誠真 )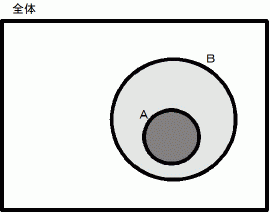
 基本包含命題は、 必ず「 もし主語が集合Xに属するならば、 主語は
基本包含命題は、 必ず「 もし主語が集合Xに属するならば、 主語は集合Yに属する。」という形をとります。
逆 :
「 もし吾輩が動物であるならば、 吾輩は猫である。」
( 真なので真は
 真 )
真 )
 吾輩が猫の場合は真になり、 吾輩が犬の場合は偽になります。
吾輩が猫の場合は真になり、 吾輩が犬の場合は偽になります。これは、 逆包含関係の ( 真なので真は
 真 )になっています。
真 )になっています。裏 :
「 もし吾輩が猫でないならば、 吾輩は動物でない。」
( 真なので真は
 真 )
真 )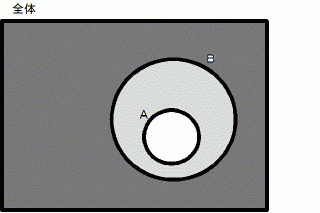
 吾輩が猫の場合は真になり、 吾輩が犬の場合は偽になります。
吾輩が猫の場合は真になり、 吾輩が犬の場合は偽になります。これは、 順包含関係の ( 偽なので偽は
 真 ) になっています。
真 ) になっています。対偶 :
「 もし吾輩が動物でないならば、 吾輩は猫ではない。」
( 真なので真は
 誠真 )
誠真 )
 これは、 逆包含関係の ( 偽なので偽は
これは、 逆包含関係の ( 偽なので偽は  誠真 ) になっています。
誠真 ) になっています。基本の包含命題と対偶は、 哲学の世界では必ず真になります。 このことを、 基本の包含命題が逆包含関係になっている場合で確かめてみましょう。 たとえば、「 もし吾輩が動物ならば、 吾輩は猫ある。」( 真なので真は
 真 ) のときは、 対偶命題は「 もし吾輩が猫でなければ、 吾輩は動物ではない。」( 真なので真は
真 ) のときは、 対偶命題は「 もし吾輩が猫でなければ、 吾輩は動物ではない。」( 真なので真は  真 ) です。 また、 現実の世界や数学の世界においては、 基本の包含命題と対偶は、 必ず真と偽が一致します。 もし、 犬が次のような命題を言ったとしましょう。「 もし吾輩が動物ならば、 吾輩は猫である。」これは明らかに偽です。 この対偶命題は「 もし吾輩が猫でなければ、 吾輩は動物ではない。」ですので、 明らかに偽です。
真 ) です。 また、 現実の世界や数学の世界においては、 基本の包含命題と対偶は、 必ず真と偽が一致します。 もし、 犬が次のような命題を言ったとしましょう。「 もし吾輩が動物ならば、 吾輩は猫である。」これは明らかに偽です。 この対偶命題は「 もし吾輩が猫でなければ、 吾輩は動物ではない。」ですので、 明らかに偽です。-
集合の包含関係に「 必要条件 」や「 十分条件 」という言葉があります。「 猫 」という集合は「 動物 」という集合に対して「 順包含関係 」にあります。 つまり、「 猫 」は「 動物 」の部分集合です。 吾輩が猫であるための「 必要条件 」は、 吾輩が動物であることであり、 吾輩が動物であるための「 十分条件 」は、 吾輩が猫であることです。「 十分条件 」になる方が「 必要条件 」になる方に内包されています。
「 ある要素が集合Aに属するための必要条件は、 ある要素が集合Bに属することである。」という言い方 や「 ある要素が集合Bに属するための十分条件は、 ある要素が集合Aに属することである。」という言い方は、「 集合Aは集合Bの部分集合である。」という言い方 や「 集合Aは集合Bに内包されている。」という言い方と同義です。
説得力のある説明の手段に「 三段論法 」というのがあります。 それは次のような理論展開です。
 集合Aは集合Bに内包されている。
集合Aは集合Bに内包されている。 この要素は集合Aに属する。
この要素は集合Aに属する。 よって、 この要素は集合Bに属する。
よって、 この要素は集合Bに属する。これを別の言い方にすると、 次のようになります。
「 『 集合Aが集合Bの部分集合であるとき、 ある要素が集合Bに属するための十分条件は、 その要素が集合Aに属することである。』 という定理に従うと、 この要素は集合Aに属しているので、 この要素は集合Bに属していると言うことができる。」
( 例−1 )
 猫は動物である。
猫は動物である。 吾輩は猫である。
吾輩は猫である。 よって、 吾輩は動物である。
よって、 吾輩は動物である。( 例−2 )

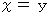 ならば
ならば 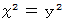 である。
である。( 変数
 と
と  に代入すると
に代入すると 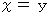 を満たす数のペアたちで構成される
を満たす数のペアたちで構成される集合は、 変数
 と
と  に代入すると
に代入すると 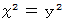 を満たす数のペアたちで
を満たす数のペアたちで構成される集合 の部分集合である。 )
 変数
変数  と
と  のペア
のペア 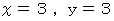 は
は 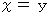 を満たす。
を満たす。 よって、
よって、 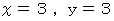 は
は 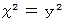 を満たす。
を満たす。三段論法の使い方を間違えると、「 吾輩は動物なので、 吾輩は猫である。」とか、「
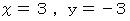 は
は 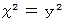 を満たすので、
を満たすので、 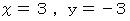 は
は 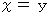 を満たす。」というように、「 必要条件 」を前件とし、「 十分条件 」を後件とし、 ベン図の内へ内へと向かっていきます。 つまり、「 集合Aが集合Bの部分集合であるとき、 ある要素が集合Aに属するならば、 その要素は集合Bに属する。」という定理を、 逆にしてしまって、「 ある要素が集合Bに属するので、 その要素は集合Aに属する可能性がある。」と言わなければならないところを、「 その要素は集合Aに属する。」と断言してしまうのです。 したがって、 三段論法の間違った使用方法は、 しばしば間違った結論に我々を導きます。
を満たす。」というように、「 必要条件 」を前件とし、「 十分条件 」を後件とし、 ベン図の内へ内へと向かっていきます。 つまり、「 集合Aが集合Bの部分集合であるとき、 ある要素が集合Aに属するならば、 その要素は集合Bに属する。」という定理を、 逆にしてしまって、「 ある要素が集合Bに属するので、 その要素は集合Aに属する可能性がある。」と言わなければならないところを、「 その要素は集合Aに属する。」と断言してしまうのです。 したがって、 三段論法の間違った使用方法は、 しばしば間違った結論に我々を導きます。なお、 三段論法は「 証明 」ではありません。 証明 と 三段論法 との関係について言えば、 三段論法の
 の部分を明らかにすることが証明であると言えましょう。
の部分を明らかにすることが証明であると言えましょう。 次のページへ進む
次のページへ進む