(8) 法則の証明
-
全体集合になっているその集合の条件を「 法則 」 と言うことにします。 公理や定理も法則に含まれます。 法則には、 全体集合の条件が重要になります。 例えば、「 数は2乗すると0以上の数になる。」 というのが法則になるためには、 全体集合の条件が実数であることが必要になります。 ある集合が全体集合になっていることの証明の方法の1つは、 その集合が包含する部分集合が全体集合になっていることを明らかにすることです。
たとえば、 全体集合が、 次のような変数
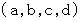 の6組のカルテットであるとします。
の6組のカルテットであるとします。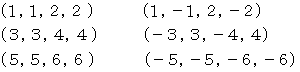
 変数
変数 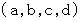 にそれぞれの値を代入したときに、
にそれぞれの値を代入したときに、 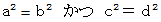
を満たすカルテットたちで構成される集合を集合Aとする。
 変数
変数 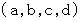 にそれぞれの値を代入したときに、
にそれぞれの値を代入したときに、 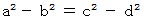
を満たすカルテットたちで構成される集合を集合Bとする。
 集合Aは集合Bの部分集合である。
集合Aは集合Bの部分集合である。(
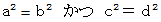 ならば
ならば 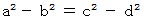 である。)
である。) 集合Aは全体集合である。
集合Aは全体集合である。 したがって、 集合Bは全体集合である。
したがって、 集合Bは全体集合である。 したがって、
したがって、 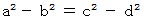 はこの全体集合の条件の下で法則である。
はこの全体集合の条件の下で法則である。もし全体集合の中に
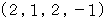 というカルテットが入ってきた場合は、
というカルテットが入ってきた場合は、 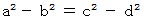 は法則ではありますが、 それが証明されたことにはなりません。 なぜならば、
は法則ではありますが、 それが証明されたことにはなりません。 なぜならば、 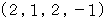 は集合Aに属さないので、 集合Aは全体集合ではなくなるからです。
は集合Aに属さないので、 集合Aは全体集合ではなくなるからです。-
問題1 :
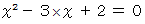 を解け。
を解け。-
その解答が
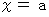 であると仮定すると、 次の命題Aは真である。
であると仮定すると、 次の命題Aは真である。命題A : 「
 は、 変数
は、 変数  に代入すると
に代入すると 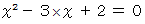 を満足する数で構成
を満足する数で構成される集合に属する。」
命題Aが真であるための必要十分条件は、 次の命題Bが真であることである。
命題B : 「
 は、 変数
は、 変数  に代入すると
に代入すると 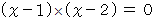 を満足する数で構
を満足する数で構成される集合に属する。」
命題Bが真であるための必要十分条件は、 次の命題Cが真であることである。
命題C : 「
 は、 変数
は、 変数  に代入すると
に代入すると 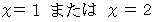 を満足する数で構
を満足する数で構成される集合に属する。」
「 変数
 に代入すると
に代入すると 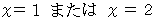 を満足する数 」 は、
を満足する数 」 は、  または
または 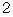 であるので、
であるので、  は
は  または
または 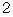 である。
である。したがって、 この問題の解答は
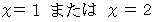 である。
である。 についての恒等式
についての恒等式 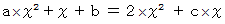 が成り立つような
が成り立つような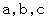 の値を求めよ。
の値を求めよ。-
解答が
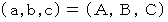 であると仮定すると、 次の命題Aは真である。
であると仮定すると、 次の命題Aは真である。命題A :「
 に代入すると
に代入すると 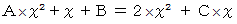 を満足する数で構成
を満足する数で構成される集合は、 全体集合である。」
命題Aが真であるための必要十分条件は、 次の命題Bが真であることである。
命題B :「
 に代入すると
に代入すると 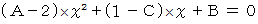 を満足する数で構
を満足する数で構成される集合は、 全体集合である。」
命題Bが真であるための必要十分条件は、 次の明らかに真である命題Cと命題Bが同一の命題であることである。
命題C :「
 に代入すると
に代入すると 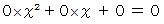 を満足する数で構成される集合
を満足する数で構成される集合は、 全体集合である。」
命題Cと命題Bとが同一になるための必要十分条件は、 次の式が成り立つことである。
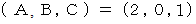
したがって、 この問題の解答は
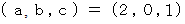 である。
である。 についての方程式
についての方程式 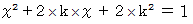 が少なくとも1つの正の解
が少なくとも1つの正の解を持つように
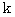 の範囲を定めよ。
の範囲を定めよ。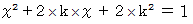 の解を
の解を 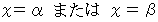 と仮定する。
と仮定する。ここで、
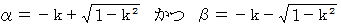 と置く。
と置く。 ただし、 2次方程式の解の公式を用いた。
ただし、 2次方程式の解の公式を用いた。すると、次のようになる。
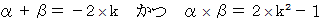
さて、
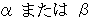 のどちらかが正の数になるための必要条件は、 次の式が成立することである。 なぜなら、 2つともが複素数の解では駄目だから。
のどちらかが正の数になるための必要条件は、 次の式が成立することである。 なぜなら、 2つともが複素数の解では駄目だから。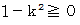
この式が成立するための必要十分条件は、 次の式が成立することである。

さて、 題意を満たすための必要十分条件は次の様なものである。
「 この方程式が、
 2つの正の解を持つ、 または、
2つの正の解を持つ、 または、
 と 1つの正の解を持つ、 または、
と 1つの正の解を持つ、 または、 異符号の解を持つ 」
異符号の解を持つ 」 が成立するための必要十分条件は、 次のようなものである。
が成立するための必要十分条件は、 次のようなものである。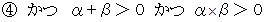
そのための必要十分条件は、 次のようなものである。
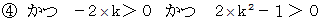
そのための必要十分条件は、 次のようなものである。
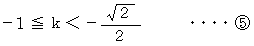
 が成立するための必要十分条件は、 次のようなものである。
が成立するための必要十分条件は、 次のようなものである。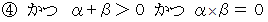
そのための必要十分条件は、 次のようなものである。
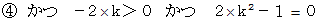
そのための必要十分条件は、 次のようなものである。
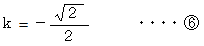
 が成立するための必要十分条件は、 次のようなものである。
が成立するための必要十分条件は、 次のようなものである。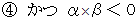
そのための必要十分条件は、 次のようなものである。
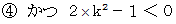
そのための必要十分条件は、 次のようなものである。
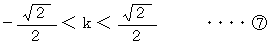
 または
または  または
または  より、 答えは次のようになる。
より、 答えは次のようになる。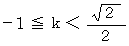
 この論文のトップへ戻る
この論文のトップへ戻る