（１） はじめに

　「 置換 」のうち、 すべての要素が異なる要素に変換される置換を「 完全順列置換 」と言うことにします。「 完全順列 」とは、 第 ｎ 項が ｎ でない数列です。「 完全順列置換 」の方法が全部で何通りあるのか、 要素の数を １ から１つずつ増やしていったときの結果を数列にしたものは、「 モンモール数列 」と言われています。

　　　　　　

（２） 門モールでのクリスマス会

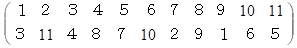
　 それぞれが会費４千円と千円相当のプレゼントを用意して、 19時に門モールの欄烈という飲食店に集まりました。 クリスマス会も終わりに近づいたころ、 恒例の「 プレゼント交換会 」が始まりました。 11個のクリスマスプレゼントがテーブルの上に置かれています。 大きなもの小さなもの、 どれを選ぼうかみんな狙いを定めようとしています。

　 そこへ無作為に １ 〜 11 の番号札11枚のうち１枚づつ各参加者に配られます。 １番札をもらった人は立ち上がるとすぐプレゼントを１つ選んで自分のものとしました。 ルールは、 自分が持参したもの以外を１つ選ぶことです。 次にプレゼントを選べるのは、 ２番の番号札を持っている人ではなく、 今選ばれたプレゼントを持参してきた人です。 もし、 その人が既にプレゼントを選んでいた場合には、 残っている人の中で一番小さな数の番号札を持っている人がプレゼントを選ぶことになります。

　ではここで問題です。 全部で何通りのプレゼントのもらい方があるでしょうか？　自分が持参したものも選んでよいのなら、 11 !　であり、 簡単なのですが ・ ・ ・ ・ 。 そこで、 参加者が少ない場合について考えてみましょう。 参加者が１人の場合は ０ とおり、 ２人の場合は １ とおり、 ３人の場合は ２ とおり、 ４人の場合は ９ とおり。 ここまででくたびれてしまいます。

　 参加者が ｎ 人のときの全ての場合の数を Ｓ （ ｎ ） とします。

　 １番札をもらった人に選ばれたプレゼントを持参した人が、 １番札をもらった人の持参したプレゼントを選ぶ場合は、 彼がプレゼントを選んだ直後から ｎ−２ 人による新たな 「 プレゼント交換会 」 が始まると考えることができます。 そして、 ２番目にプレゼントを選ぶことになる人については、 ｎ−１ 通りありますので、 １番札をもらった人に選ばれたプレゼントを持参した人が、 １番札をもらった人の持参したプレゼントを選ぶ場合は、 全ての場合の数は次のようになります。
　　　　　Ｓ（ ｎ−２ ）×（ ｎ−１ ）

　 １番札をもらった人に選ばれたプレゼントを持参した人が、 １番札をもらった人の持参したプレゼントを選ばない場合は、 彼が残りのプレゼントから選ばないのは、 １番札をもらった人が持参したプレゼントだけであり、 他の人が自分の持参したプレゼントだけ選ばないのと同等の行為をすることですので、 彼がプレゼントを選ぶ直前から ｎ−１ 人による 新たな「 プレゼント交換会 」が始まると考えることができます。 そして、 ２番目にプレゼントを選ぶことになる人については、 ｎ−１ 通りありますので、 １番札をもらった人に選ばれたプレゼントを持参した人が、 １番札をもらった人の持参したプレゼントを選ばない場合は、 全ての場合の数は次のようになります。
　　　　　Ｓ（ ｎ−１ ）×（ ｎ−１ ）

　 以上の２つの場合ですべてのケースが網羅されていますので、 求めるすべての場合の数 Ｓ（ ｎ ）は次のようになります。
　　　　　Ｓ（ ｎ ） ＝ （ ｎ−１ ）｛ Ｓ（ ｎ−１ ）＋ Ｓ（ ｎ−２ ） ｝

　 これから先は、 次のようなプログラムを作ってコンピューターに計算してもらいましょう。


　　※　Ｓ（ ｎ ） ＝ （ ｎ−１ ）｛ Ｓ（ ｎ−１ ）＋ Ｓ（ ｎ−２ ）｝　の解法については、　確率 ＞ 確率 e 分 の 1　を参照ください。

　　※　モンモールの出会いについては、　確率 ＞ 位の数がすべて異なる確率　を参照ください。