高さと直径が 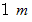の円柱の体積を物理学的方法で求めるには、 実物大の円柱を型にして鍋を作り、 それを満杯にする水の質量を測定してそれを とし、 とし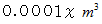て求めます。

　 以上のような物理的な方法で、 近似的に の値を求めることができます。 それには乱数表の中から何度も数字の標本を取り出すという実験が必要です。 そこで、 それを手早くするためにパソコンを利用します。 次のＣ言語のプログラムをご覧ください。

#include < stdio.h >
#include < stdlib.h >

int random ( int min, int max );

main ( )
{
　　int i, n ;
　　int x, y ;
　　double p ;
　　n = 0 ;
　　printf ("円周率 ( 3.14159 ) を求めています。 しばらくお待ち下さい。\n\n") ;
　　for ( i = 0 ; i <= 10000000 ; i++ ) {
　　　　　x = random ( -1000, 1000 ) ;
　　　　　y = random ( -1000, 1000 ) ;
　　　　　if ( ( x * x + y * y ) < 1000000 ) {
　　　　　　　　n++ ;
　　　　　　　　　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　　　　　　　　}
　　p = 4.0 * n / 10000000.0 ;
　　printf ("円周率は、 およそ %f です。\n\n", p ) ;
　　return 0 ;
}

int random ( int min, int max )
{
　　return min + ( rand ( ) * ( max - min + 1.0 ) / ( 1.0 + RAND_MAX ) ) ;
}

　 これは何をしているのかというと、 辺の長さが 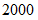の正方形の内部の点をアットランダムに抽出した時にその点がこの正方形の内接円の中に存在する確率を一千万回の実験により求め、 それが理論的には になっているはずだからということで、 を求めているのです。 このように、 乱数を用いて数値を求めたりシミュレーションを行ったりする手法を、 モンテカルロ法 と言います。 この手法は、 中性子が物質中を動き回る様子を探ろうと、 ジョン・フォン・ノイマンによって考案されました。


モンテカルロ法にて、 小数点以下７桁の π の近似値を示します。

　　　        

　　３種類のプログラム ：

「 ビュフォンの針 」という有名な 落下位置の確率問題 があります。

　　　　　　＊　参照 ：　大学生のための数学 ＞ 確率 ＞ 落下位置の確率（ ビュフォンの針 ）

これ利用してモンテカルロ法で π の近似値を求めるプログラムを紹介します。

床に４ｃｍの間隔で平行な直線を多数描きます。
そこへ長さ２ｃｍの針を放り投げたとき、 針が直線のどれかに接する確率は、
０ ≦ y ≦ ２　かつ　０ ≦ θ ≦ π/２　の範囲で 無作為に
y と θ の値を決めたときに、 次の式が成り立っている確率である。
　　　y　≦　sin θ
したがって、 その確率は、
sin θ を ０ ≦ θ ≦ π/２ の範囲で定積分したものを π で割ったもの
になる。 つまり １/π になる。 したがって、
　　　π　≒ 　１ / （ シミュレーションで求めた確率 ）

　　　

　　　π　≒