ニュートン法を他のケースでも用いることができるようにするために、 一般化しておきましょう。 関数
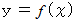 が微分可能で下に凸であるとき、
が微分可能で下に凸であるとき、 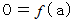 を満たす
を満たす  を求めるものとします。
を求めるものとします。まず、
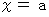 に近い
に近い 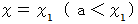 をとり、
をとり、 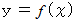 上の点
上の点 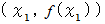 で接する接線を求めます。 すると、 次のようになります。
で接する接線を求めます。 すると、 次のようになります。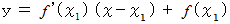
この接線が
 軸と交わる点の
軸と交わる点の  座標を求めます。
座標を求めます。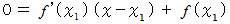 より、
より、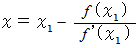 これを
これを 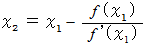 と置きます。
と置きます。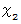 は
は 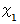 よりもさらに
よりもさらに  に近くなっています。
に近くなっています。次に、
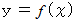 上の点
上の点 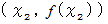 で接する接線を求める。 すると、 次のようになります。
で接する接線を求める。 すると、 次のようになります。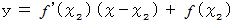
この接線が
 軸と交わる点の
軸と交わる点の  座標を求めると、 次のようになります。
座標を求めると、 次のようになります。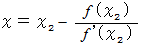 これを
これを  と置きます。
と置きます。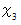 は
は 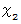 よりもさらに
よりもさらに  に近くなっています。
に近くなっています。一般的には、
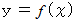 上の点
上の点 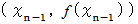 で接する接線を求め、 この接線が
で接する接線を求め、 この接線が  軸と交わる点の
軸と交わる点の  座標を求めると、 次のようになります。
座標を求めると、 次のようになります。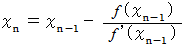
 が大きくなるほど
が大きくなるほど 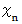 は
は  に近くなっていきます。
に近くなっていきます。 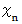 を数列とみなしますと、 上記の式は漸化式になっています。
を数列とみなしますと、 上記の式は漸化式になっています。ここで、 例えば、
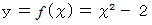 の場合を考えます。
の場合を考えます。 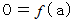 を満たす
を満たす  、 つまり、
、 つまり、 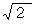 を求めるものとします。 漸化式は次のようになります。
を求めるものとします。 漸化式は次のようになります。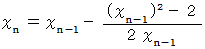
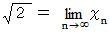 ですから、 この漸化式を用いて
ですから、 この漸化式を用いて 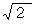 の近似値を求める十進BASIC のプログラムを作りますと、 次のようになります。
の近似値を求める十進BASIC のプログラムを作りますと、 次のようになります。 次のページへ進む
次のページへ進む