（５） 運動方程式 から「 質点の運動量モーメント保存の法則 」を導く

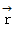　 の物質の位置ベクトルを とします。 物質には力 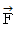が作用しているとします。 すると、 この物質に関する運動方程式は次のようになります。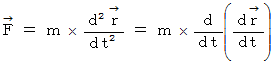
　　　　
この両辺に 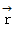を外積させるという演算を施します。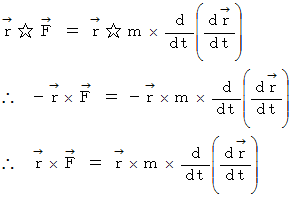
　　　　
　 さて、 ここ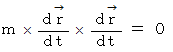で、 　ですので、 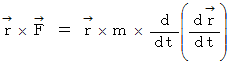　が成り立つための必要条件は、 次の式が成り立つことです。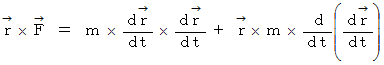
　　　　
この式の右辺は次のように変形されます。
　　　　
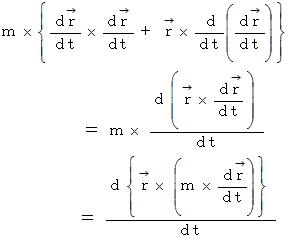
したがって、次のようになります。
　　　　
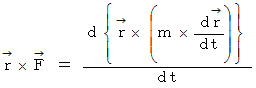
　 この式の左辺は 位置ベクトルの基点を支点とする「 力のモーメント 」で、 右辺は「 運動量モーメント（ 角運動量ではありません ）」を時間で微分したものです。
この式は、 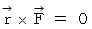のとき、 次のようになります。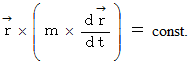
　　　　
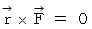　 とは、 力が作用していないとき、 または、 物質に作用する力の方向が、 公転の焦点から物質への位置ベクトルの向きと同じかまたは逆のときです。 したがって、 「 質点の運動量モーメントが変化しないための必要条件は、 質点に対して力のモーメントが作用しないことである。」 ということが解ります。

（６） 運動量保存の法則

　 運動方程式は、 次のように変形されます。
　　　　　
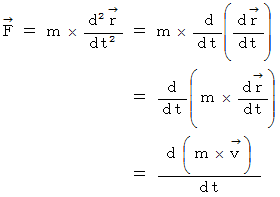
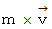　 は運動量です。 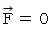のとき　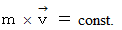 になります。
　 以上より、「 力が作用しなければ、 物質は、 同じ運動量を保ったまま運動し続ける。」ということがわかります。 これは「 運動量保存の法則 」とは違います。 これは、「 力が作用しなければ、 物質は、 同じ速度を保ったまま運動し続ける。」という「 慣性の法則 」と同義です。
　 一般的な「 運動量保存の法則 」とは、「 外力が作用しない限り、 その系の運動量は一定に保たれる。」というものです。

（７） 運動エネルギー保存の法則

　「 非等速直線運動 」における運動方程式を用意します。 運動は１次元ですから、 ベクトルを用いる必要はなく、 運動方程式は次のように実数で表すことができます。
　　　　
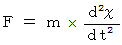
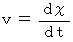ですので、 上の式は次のようにも表すことができます。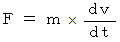
　　　　
　 まず、 運動エネルギーが　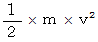　で表されることを導いてみましょう。
上の式より、 次の式が成り立ちます。
　　　　

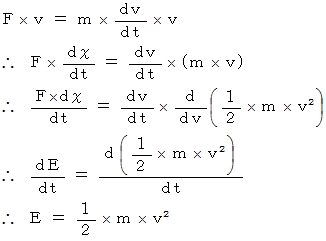
　 次に、 運動エネルギーを 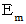とすると、 これまでのことから、 次の式が成り立つことが解ります。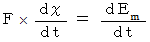
　　　　
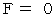　　　　 のとき、 次の式が成り立ちます。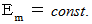
　　　　　　　　

　 以上より、「 力が作用しなければ、 物質は同じ運動エネルギーを保ったまま運動し続ける。」ということがわかります。 これは「 運動エネルギー保存の法則 」と言ってもいいと思います。
　 一般的なのは「 力学的エネルギー保存の法則 」です。 これは、運動エネルギーと位置エネルギーの和が一定であるというものです。