第２章 変速度運動も相対的なものである。
「 物質の空間移動 」は、「 物質 」と「 観察者 」の２つで構成されます。「 物質 」の移動 と「 観察者 」の移動 とは、「 慣性系 」においては相対的なものです。 相対的であるという１つ目の意味は、「 どっちが移動していて、 どっちが静止しているのか？ 」ということは区別がつかないし、 そういうことは物質の空間移動にとってはどうでもいいことだ、 ということです。 この事実は「 『 絶対的静止 』 は存在しない。」とも表現されます。 ２つ目の意味は、 観察される物質が観察者になり、 観察者が観察される物質になった場合、 物質 と 観察者 が向かい合っていれば、 相手の移動の内容は全く同じものであるということです。
こういった事実は、「 慣性系 」のみならず、「 変速度系 」においても成り立っています。 私は、 このような「 移動の相対性 」を、 次のように、 ４つにまとめて、 それぞれ名前をつけています。
【 １ 】 相対的等速度運動の公理
物質Ａ と 物質Ｂ がそれぞれ異なる速度で等速直線運動（ 静止を含む ）をしている。 このとき、 物質Ａ または 物質Ｂ の立場に立ってみると、 次の２つの命題はともに真である。
１． 物質Ａは静止していて、 物質Ｂは等速直線運動をしている。
２． 物質Ｂは静止していて、 物質Ａは等速直線運動をしている。
また、 このときの 物質Ａ と 物質Ｂ の運動関係を、「 物質Ａ と 物質Ｂ は相対的等速度運動をしている。」と言う。
【 ２ 】 相対的変速度運動の公理
ロケットＡ と ロケットＢ が それぞれ異なる速度で等速直線運動（ 静止を含む ）をしていた。 突然、 ロケットＡのみが変速度運動を開始した。 その後、 ロケットＡ または ロケットＢ の立場に立ってみると、 次の２つの命題はともに真である。
１． ロケットＢは静止していて、 ロケットＡは変速度運動をしている。
２． ロケットＡは静止していて、 ロケットＢは変速度運動をしている。
また、 このときの 物質Ａ と 物質Ｂ の運動関係を、「 物質Ａ と 物質Ｂ は相対的変速度運動をしている。」と言う。
＊ コメント： 「 相対的変速度運動の公理 」は、「 運動関係 」について言ったもので、
移動の方法まで考えた時には、 相対性が崩れる場合があります。 たとえば、
ロケットエンジンなどにより「 自力変速度運動 」が行われる場合には、 相
対性が崩れます。 なぜなら、 一方にのみ静止質量の減少が生じるからです。
また、「 押し上げ変速度運動 」による場合にも相対性が崩れます。 なぜ
なら、「 押し上げ変速度運動 」を被っている方は、 本人を「 重力固定者 」
と認識し、 相手を「 落下中の人 」と認識するのに対して、 そうでない方は、
本人を「 無重力状態 」と認識し、 相手を「 押し上げ変速度運動 」を被って
いる人 と認識するからです。
「 押し上げ変速度運動 」とは、 箱の中の物質が加速的変速度運動をす
る箱の底から力を受けて、 箱と同じ変速度運動をすることです。
「 重力固定物質 」とは、 地上に置いてある物質のように、 重力への反作
用が働いて落下していない物質のことです。
【 ３ 】 一様等速運動付加の公理（ 運動関係保存の第１法則 ）
１． 物質Ａ と 物質Ｂ がそれぞれ異なる速度で相対的等速直線運動（ 静止を含む ）をしている。 それを、 物質Ａに対して一定の速度
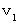で移動している人 と 物質Ａに対して一定の速度 
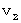で移動している人 とが観察したのでは、 ２つの物質の速度が変わってくる。 ただし、 ２つの物質とも等速直線運動（ 静止を含む ）をしているということは共通する。また、 このとき、 物質Ａ または 物質Ｂ の立場に立ってみると、 物質Ａ と 物質Ｂ は今まで通りの相対的等速度運動を続ける。（ 物質Ａ と 物質Ｂ の運動関係は不変である。）
２． 物質Ａ と 物質Ｂ が相対的変速度運動をしている。 それを、 物質Ａに対して一定の速度
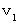で移動している人 と 物質Ａに対して一定の速度 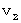で移動している人 とが観察したのでは、 ２つの物質の速度が変わってくる。 ただし、 物質Ａは等速直線運動をしており、 物質Ｂは変速度運動をしているということは共通する。また、 このとき、 物質Ａ または 物質Ｂ の立場に立ってみると、 物質Ａ と 物質Ｂ は今まで通りの相対的変速度運動を続ける。（ 物質Ａ と 物質Ｂ の運動関係は不変である。）
【 ４ 】 一様変速度運動付加の公理（ 運動関係保存の第２法則 ）
１−１． 物質Ａ と 物質Ｂ が相対的等速直線運動をしている。 この状態が２つの物質に対して
変速度運動をしている観察者によって観察されると、 ２つの物質とも同等の変速度運動
をしていることになる。
このとき、 物質Ａ または 物質Ｂ の立場に立ってみると、 物質Ａ と 物質Ｂ は今まで通
りの相対的等速直線運動を続ける。 （ 物質Ａ と 物質Ｂ の運動関係は不変である。）
１−２． 物質Ａ と 物質Ｂ が相対的等速直線運動をしている。 突然、 ２つの物質に、 力が働
き始めた。 その力は、 方向が同じで、 大きさが質量に比例する。（ 一様な重力場は、
物質に対してこのような力を及ぼす。） すると、 ２つの物質は、 同等の変速度運動を開
始する。
このとき、 物質Ａ または 物質Ｂ の立場に立ってみると、 物質Ａ と 物質Ｂ は今まで通
りの相対的等速直線運動を続ける。（ 物質Ａ と 物質Ｂ の運動関係は不変である。）
２−１． 物質Ａ と 物質Ｂ が相対的変速度運動をしている。 この状態が 物質Ａ または 物質Ｂ
に対して変速度運動をしている観察者によって観察されると、 ２つの物質には、 同等の
変速度が追加され、 変速度が変化したり消失したりする。
このとき、 物質Ａ または 物質Ｂ の立場に立ってみると、 物質Ａ と 物質Ｂ は今まで通
りの相対的変速度運動を続ける。（ 物質Ａ と 物質Ｂ の運動関係は不変である。）
２−２． 物質Ａ と 物質Ｂ が相対的変速度運動をしている。 突然、 ２つの物質に、 力が働き
初めた。 その力は、 方向が同じで、 大きさが質量に比例する。（ 一様な重力場は、 物
質に対してこのような力を及ぼす。） すると、 ２つの物質には、 同等の変速度が追加さ
れ、 変速度が変化したり消失したりする。
このとき、 物質Ａ または 物質Ｂ の立場に立ってみると、 物質Ａ と 物質Ｂ は今まで通
りの相対的変速度運動を続ける。（ 物質Ａ と 物質Ｂ の運動関係は不変である。）
第３章 光も変速度運動をする。
第２章で述べた「 一様変速度運動付加の公理（ 運動関係保存の第２法則 ）」の中の １−１． と １−２. との区別ができないことを、「 等価原理 」と言っていいように思われますが、 しかし、 これだけでは不十分です。 何故かというと、 光の運動も区別できないということに触れられてないからです。
（１）思考実験その１： ボーリング場にて
-
思い浮かべてください。 立方体の箱が置いてあります。 箱のふたを開けると、 底に小人（ こびと ）が寝転がっています。 彼の身長は立方体の辺の長さの半分くらいで、 両足底は１つの側壁に接触しています。 また、 箱の底の真ん中には小さな穴が開いており、 穴のそばには、 天に向かって垂直に赤い光を放つレーザー発生装置があります。 そっと箱のふたを閉じましょう。 次に、 ボーリングのレーンを思い浮かべてください。 レーンの真ん中あたりには、 １箇所、 レーザー発生装置が埋め込まれています。 それは天に向かって垂直に紫の光を放ちます。
さて、 さっきの箱をレーンの上で滑らせます。 小人の頭が常に１０本のピンを向くようにして等速直線運動させます。 箱の底の穴がレーンに埋め込まれたレーザー発生装置の真上にきた瞬間、 ２つのレーザー発生装置から同時にレーザー光が放たれました。 すると、 小人は、 赤と紫のレーザー光をそれぞれどのように観察するでしょうか？ （ これを シチュエーション１ とします。）
答えは、「 赤色は、 天頂に向かう直線。 紫色は、 天頂の少し足寄りに向かう直線。」です。
では次に、 箱を帯電させます、 プラスの電荷に。 そして、 １０本のピンを固定してマイナスの電荷に帯電させます。 さあ、 先程と同様にして、 箱を滑らせましょう。 すると、 今度は、 箱はレーンの上を加速的変速度運動します。 箱の底の穴がレーンに埋め込まれたレーザー発生装置の真上にきた瞬間、 ２つのレーザー発生装置から同時にレーザー光が放たれました。 すると、 小人は、 赤と紫のレーザー光をそれぞれどのように観察するでしょうか？ （ これを シチュエーション２ とします。）
答えは、「 赤色は、 最初は天頂に向かう曲線（ 少し足寄りに曲がる ）。 紫色は、 最初は天頂の少し足寄りに向かう曲線（ 赤色よりもさらに足寄りに曲がる ）。」です。
その次に、 今度は、 箱と小人をプラスの電荷に帯電させます。 ただし、 その電荷量はそれぞれの質量に比例するように設定します。 そして、 １０本のピンを固定してマイナスの電荷に帯電させます。 さあ先程と同様にして、 箱を滑らせましょう。 レーンの上を加速的変速度運動させるのです。箱の底の穴がレーンに埋め込まれたレーザー発生装置の真上にきた瞬間、 ２つのレーザー発生装置から同時に真上に向けてレーザー光が放たれました。 すると、 小人は、 赤と紫のレーザー光をそれぞれどのように観察するでしょうか？ （ これを シチュエーション３ とします。）
答えは、「 赤色は、 最初は天頂に向かう曲線（ 少し足元寄りに曲がる ）。 紫色は、 最初は天頂の少し足寄りに向かう曲線（ 赤色よりもさらに足元寄りに曲がる ）。」です。 これは、 シチュエーション２ と全く同じで区別がつきません。
これから、 それぞれのシチュエーションを検討・解説していきます。
【 シチュエーション１ 】
-
レーザー光は、 物質と同様、 発射される時の母体の運動を背負って運動します。 レーンに固定されたレーザー発生装置から発射されるレーザー光は、 紫色のレーザー光を発射する時、 小人に対して、 彼の頭から足の方向へ等速直線運動しています。 したがって、 紫色のレーザー光は小人の天頂の少し足寄りの方向に直進します。
-
シチュエーション１ に、 小人の足下へ向く一様な重力場が加わったような状況によく似ています。 このとき、 光も重力を受けているかのようで、 その軌跡は放物線を描きます。 小人は「 重力 」を感じ、 足を突っ張って立っていると言ってもいいでしょう。 小人自身は、 決して自分が変速度運動をしているとは思っていません。 小人の変速度運動は、 箱の運動によるもの、 あるいは箱からの力によるものです。
-
シチュエーション１ に、 小人の足下へ向く一様な重力場が加わったような状況によく似ています。（ ただし、 小人には重力が作用していない状況です。）このとき、 光も重力を受けているかのようで、 その軌跡は放物線を描きます。 小人自身は、 頭 ⇔ 足 方向に対しては浮いていると思っています。
-
思い浮かべてください。 今、 宇宙空間に１つの天体があります。 その天体に向かって、 弓が落下運動しています。 弓は、 落下の方向に対して垂直な方向（ これを水平方向とします ）に、 いつでも矢を放てる状態になっています。 あなたはその弓と一緒に足のほうから落下運動しています。 また、 小人（ こびと ）が２人いて、 小人のＡ君は、 直接「 神の手 」によって重力と同じ大きさで反対方向に引っ張られており、 小人のＢ君は、 箱の中にいて、 その箱が「 神の手 」によって重力と同じ大きさで反対方向に引っ張られています。 彼らの足は天体の重心を向いており、 天体に対して静止しています。 そして、 弓が小人に対して速さ
になった瞬間に、 矢が放たれました。【 あなたの観察内容 】
-
弓 ： 静止
矢 ： 水平方向に等速直線運動
-
弓 ： 変速度直線運動
矢 ： ほぼ放物線の軌跡
・ 垂直方向には、 下に向かう初速が
の加速的変速度運動・ 水平方向には、 ほぼ等速運動
（ 正確には、 相対的垂直速度の法則により、 若干の減速運動 ）
＊ コメント ： 相対的垂直速度の法則
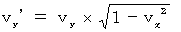
【 あなたの観察内容 】
-
レーザー銃 ： 静止
レーザー光 ： ほぼ放物線の軌跡
・ 垂直方向には、 上に向かう初速 ０ の変速度運動
・ 水平方向には、 ほぼ等速運動
（ 正確には、 相対的垂直速度の法則により、 若干の減速運動 ）
しかし、 レーザー光の軌跡は、 間違いです。「光の静止質量は ０ だから、 重力は働かない。 だから、 レーザー光は垂直方向に、 あなたに対して相対的変速度運動をする。」と単純に考えたための間違いです。 確かに光には重力は働かないのですが、 重力により空間が曲げられており、 その曲った空間を光は最短距離で伝わるという性質があるのです。
正解は、 矢と似ていて、 水平方向への 速さ １ の等速直線運動です。
＊ コメント ： 私は次のような自然現象を次のように言っています。
「 重力場曲空間の公理 」： 重力場は空間を重力場の方向に曲げる。
「 光最短伝達の公理 」： 光は空間を最短距離で伝わる。
-
レーザー銃 ： 変速度直線運動
レーザー光 ： 速さ １ の等速直線運動
・ 垂直方向には、 下に向かう速さ
の等速度運動・ 水平方向には、 速さ
の等速運動しかし、 これも、 レーザー光の軌跡が間違っています。 確かに光には重力は働かないのですが、「 重力場曲空間の公理 」と「 光最短伝達の公理 」のために、 光は曲って伝わるのです。
正解は、 矢と似ていて、 ほぼ放物線の軌跡です。
・ 垂直方向には、 下に向かう、 初速が
の変速度運動・ 水平方向には、 ほぼ等速運動
（ 正確には、 相対的垂直速度の法則により、 若干の減速運動 ）
小人たちにとってのレーザー光の軌跡を、 ボーリング場の思考実験の紫色のレーザー光と比べてみましょう。 小人のＡ君は、 ボーリング場のシチュエーション３ と この落下運動 とを区別することができません。 小人のＢ君は、 ボーリング場のシチュエーション２ と この落下運動 とを区別することができません。 これらは、「 等価原理 」です。
「 重力レンズ効果 」 という現象があります。 それは、 重力場によって光が曲げられる現象です。
光の変速度は、 次のような性質を持っています。
「 光の変速度は、 万物と同様で、 重力場に等しい。」
私は、 これを「 光変速度の公理 」と言っています。