ばいおりん の 変速度系相対性理論の足場
 ばいおりんのその他の相対論関連論文集 に戻る
ばいおりんのその他の相対論関連論文集 に戻る
 ばいおりんの慣性系相対性理論 に行く
ばいおりんの慣性系相対性理論 に行く
 ホームページのトップへ 戻る
ホームページのトップへ 戻る
2008.03.13
目 次
は じ め に ( 慣性系相対性理論のエッセンス )
第 1章 ニュートン力学 と 相対論的力学
第 2 章 変速度運動も相対的なものである。
第 3 章 光も変速度運動をする。
第 4 章 慣性 と 慣性力
第 5 章 重力場も相対的なものである。
第 6 章 等価原理
第 7 章 重力場による時間経過遅延作用
第 8 章 重力赤方偏移は「重力場による時間経過遅延作用」のせい?
第 9 章
物質の移動とは、「 観察者にとって、 被観察物質の存在する空点が、 時点の変化に伴って刻々と変化すること。」です。 日常、 私たちがよく遭遇する物質の落下運動は、 速度が変化する運動で、 次の6つの因子から成り立っています。 それは、 時間、 空間、 被観察物質、 観察者、 重力、 空気抵抗力 です。 アインシュタインの特殊相対性理論は、 この6つのうちから重力と空気抵抗力を除外して、 等速度運動( 静止を含む )をしている物質に的を絞ることにより、 観察者と被観察物質との相対的運動関係としての、 また、 4次元時空間移動としての「 物質の移動 」や「 電磁波の伝達 」の本質を明らかにし、「 電磁気学 」と「 ニュートン力学( そのうちの 運動の第1法則( 慣性の法則 ) と エネルギーと運動量の概念 )」とを統一的に捉えることに成功しました。
さらに、 アインシュタインの一般相対性理論は、 特殊相対性理論を慣性系から加速度系まで拡張して、「 重力 」とは何かを解明し、 残されていた「 ニュートン力学のうちの 運動の第2法則( 力と移動との関係 )と 第3法則( 作用・反作用 )の概念 」をも統一的に捉えた理論です。
一般相対性理論の基礎的な公理には次のようなものがあります。 私なりにアレンジして表現してみました。
1. 一般相対性原理
物質の物理学的な現象については、 どのような形態の移動をしている観察者が観察しよ
うとも、 同じ物理学的法則が成立する。
2. 一般的光速一定の公理
真空を伝わる光の速さは、 どのような形態の移動をしている観察者が観察しようとも、 一
定である。
3. 等価原理
「 一様な重力場によって生じる変速度運動 」と「 相対的変速度運動 」とは区別すること
ができない。 また、 変速度( 相対的変速度を含む )の原因になる「 重力 」と「 相対的
変速度力( 慣性力 )」とは区別することはできないし、 これらの力を合成することができ
る。 また、 変速度( 相対的変速度を含む )を生み出す「 一様な重力場 」と「 相対的一
様重力場 」とは区別することはできないし、 これらを合成することができる。
4. 重力場 や「 相対的一様重力場 」は、 時空間を曲げる。
単に、 重力が光の軌道を曲げるという概念に留まらない。
一方、 特殊相対性理論の基礎になる公理は、 次の2つです。 一般相対性理論を意識して記述します。
1. 相対性原理
物質の物理学的な現象は、 どんな観察者が観察しようとも、 その観察者が観察してい
るどんな物質たちに対しても変速度運動をしていないならば、 同じ物理学的法則が成立
する。
2. 光速一定の公理
光の速さは、 どんな観察者が観察しようとも、 光源がその観察者に対して変速度運動
をしていないならば、 一定である。
特殊相対性理論の中核は、 力が全く作用しない世界での物質( 量子を含む )の移動に関する時空間の座標変換です。 特殊相対性理論の話は、 広大な宇宙の中を多くの物質たちがさまざまな方向にさまざまな速さで移動しているところから始まります。 すべての物質は慣性の法則に従って等速直線運動( 静止を含む )をしています。 今、 この光景を観察しているあなた自身も、 他の物質と同様に、 この宇宙の中で等速直線運動しています。 この状況に、 あなたのお友達があなたに対して等速で移動している状況を付け加えてください。 では、 あなたの観察内容とお友達の観察内容はどのように異なるでしょうか? それぞれの物質の移動の速度は異なります。 しかし、 ある光源が2人から同じ距離に存在した瞬間に一瞬放たれる光は、 全く同じ形態の運動をとります。 つまり、 2人にとって同じ速さで広がります。 その中に自分に到達する光子があり、 相手に到達する光子もあります。 一方、 光源の速度は、 2人の間で異なります。 こうして、特殊相対性理論の話が展開されていきます。
さて、「 慣性系 」とは、「 非加速度系 」という意味です。 ただし、「 慣性系 」は連続しない衝突による物質の移動の変化を認めていますので、 一瞬の速度の変化があってもかまいません。 ということは、「 慣性系とは、 衝突のほかに物質の運動方向や運動エネルギーを変化させるような力が作用していない座標系である。」ということができます。 一般的には、「 慣性系 」とは「 観察しているすべての物質に対して等速直線運動 ( 静止を含む ) をしている観察者の座標系 」のことです。 物質は万有引力や摩擦により加速度運動をしますので、 慣性系は、 普通、 無重力真空空間です。
ところで、 自分の座標系が慣性系である観察者に対して、 加速度運動をしている第2の観察者が、 この第1の観察者に対して、「 あなたは慣性系ではない。」と言ったとしましょう。 すると、 この発言は正しいでしょうか? 答えは、 間違いです。「 あなたの座標系は慣性系であり、 あなたを観察している私の座標系は慣性系ではない。」が正解です。 たとえば、 自由落下運動をしている人が、 一緒に落下している物質を観察しているときは、 その人の座標は慣性系になります。
私は、「 加速度 」のことを「 変速度 」と言っています。 それは、「 加速度 」には「 速さが同じ方向に次第に増していく 」というイメージがあるからです。 しかし、「 加速度運動 」はそれだけではありません。 減速運動も「 加速度運動 」に入りますし、 等速運動でも方向が変われば「 加速度運動 」です。 要するに、 力の加わる運動はすべて「 加速度運動 」になります。「 静止 または 等速度運動 ( 等速直線運動 )」以外はすべて「 加速度運動 」です。 私は、「 変速度運動 」を「 加速的変速度運動 」、「 減速的変速度運動 」、 および「 等速的変速度運動 」の3つに分類しています。
また、 私は、 特殊相対性理論という意味で「 慣性系相対性理論 」という言葉を用い、 一般相対性理論という意味で「 変速度系相対性理論 」という言葉を使っています。 これから本題に入る前に、「 変速度系相対性理論 」の土台である「 慣性系相対性理論 」のエッセンスを紹介します。 定説と異なりますので、 ご注意ください。
1. どんな慣性系においても、 万物は4次元時空間を光の速さで移動しつづけている。
4次元時空間の1つの軸は、 相対時間 である。
2. すべての慣性系で共通する絶対時間が存在する。
つまり、 物質の活動のスピードや物質の化学反応のスピードは、 座標変換にて変化
しない。
3. 物質( 電磁波も含む )と 物質 との衝突については、 衝突される物質が静止した
当事者の立場に立たなければ、 幻想を見てしまう。
4. 「 A君が見た、 B君に対するC君の速度 」とか「 A君の観察における、 B君に対す
るB君の見る光の速度 」とかいうような第3者的立場で見た速度は、 実在する速度で
はない。
5. A君とB君とC君の3人が同じ直線上を移動している。 C君の後ろからB君が追いか
け、 B君の後ろからA君が追いかけているが、 3人の間隔は次第に広がっている。
A君にとってのA君に対するB君の速さを VB/A とし、 B君にとってのB君に対するC
君の速さを VC/B とすると、 A君にとってのA君に対するC君の速さは次の( VC/A )
式で表される。
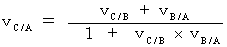
6. 「 現実化された逆ローレンツ変換 」により、「 第0観察者が観察する物質の移動す
る相対時間( それは絶対時間に等しい )」が「 第1観察者が観察する物質の移動す
る相対時間 」へと変換され、 短縮する。
* コメント :
第0観察者 ・・・ 静止している物質たちだけを観察する人
第1観察者 ・・・ 第0観察者に対して等速直線運動をしていて、 さまざ
まな第0観察者が観察している物質たちを観察する人
第2観察者 ・・・ 第1観察者に対して等速直線運動をしていて、 第1観
察者が観察している物質たちを観察する人
7. 観察される物質と観察者との相対的な移動速度の大きさの違いにより、 観察される
物質の質量が変化する。 質量は、 物質の持つエネルギーを表す。
8. 観察される光源と観察者との相対的な移動速度の大きさの違いにより、 光源から
放たれる光の空間を伝わる速さは変わらないが、 波長が変化する。
次に、「 ばいおりんの座標変換 」により、 第0観察者の慣性系からその第0観察者に対して速さ  で等速直線運動している第1観察者の慣性系へと座標変換されると、 どんな変化が起こるのか述べます。
で等速直線運動している第1観察者の慣性系へと座標変換されると、 どんな変化が起こるのか述べます。
a )観察している物質の 質量( エネルギー )
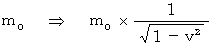
b )観察している 絶対時間( 
 )
)
変化しません。
c )観察している 
 の絶対時間に 物質が移動する 相対時間
の絶対時間に 物質が移動する 相対時間
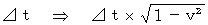
d )観察している 
 の絶対時間に 物質が移動する 空間
の絶対時間に 物質が移動する 空間
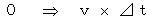
さて、 特殊相対性理論において提唱されている、 興味ある自然現象は、 次の3つです。
・ 等速直線運動をしている慣性系の中では、 時間の経過が遅くなっている。
・ 等速直線運動をしている慣性系の中では、 空間が縮んでいる。
・ 等速直線運動をしている物質は、 静止しているときよりも質量が大きい。
また、 一般相対性理論において提唱されている、 興味ある自然現象は、 次の3つです。
・ 重力場の存在する空間では、 空間が曲がっている。
・ 重力場の存在する空間では、 時間の経過が遅くなっている。
・ 重力場の存在する空間から届く光は、 波長が伸びてしまっている。
「 慣性系相対性理論の手引き 」の中で、 私は、 次のような主旨のことを述べ、 定説に反論しました。
「 A君の慣性系の中で、 等速直線運動しながら等速自転している物質がある。 この物質と並走しているBさんは、 この物質の自転をどのように観察するのか? その答えは、 ローレンツ変換を用いて求めることができる。 しかし、 こうして得た相対論的観察( Bさんによる当事者的な観察 )を ローレンツ変換前のニュートン力学的な観察( A君による第3者的観察 )と比べて、 Bさんの移動の速さが大きければ大きいほど、 Bさんの慣性系の時間の経過スピードは遅くなるという結論に達するのは間違いである。 また、 A君の慣性系の中で、 等速直線運動している棒があり、 A君は同時刻に棒の両端の位置を観察して棒の長さを測った。 この時、 この棒に並走しているBさんが棒の長さを測定するといくらになるか? その答えは、 ローレンツ変換を用いて求めることができる。 しかし、 こうして得た結果( Bさんによる非同時両端位置観察による棒の長さ )を ローレンツ変換前のA君による同時両端位置観察による棒の長さ と比べて、 Bさんの移動の速さが大きければ大きいほど、 Bさんの慣性系の空間の短縮の程度は大きくなるという結論に達するのは間違いである。」
そこで、「 変速度系相対性理論 」の中でも、 一般相対性理論の常識に挑戦してみたいと思います。 たとえば、 次のような思考実験をしてみましょう。
地球にトンネルを掘り、 地球の裏側まで落下できるような環境を作ります。 双子の兄に落下してもらいます。 兄は、 地球の裏側まで落下し、 またそこから落下して戻ってきます。 それを永遠に繰り返してもらいます。 兄の立場からすると、 兄はずっと無重力状態で、 地球と弟のほうが変速度運動をしていることになります。 さあ、 弟が1年歳をとったとき、 兄の歳はどうなっているでしょうか? この問題は「 双子のパラドックス 」と同様ではないと思いますので、 私は、 この問題のことを「 質量間力により変速度運動を行う双子のパラドックス 」と言っています。
特殊相対性理論は、「 動いている物質に対する動いている物質の相対的なみかけの速度 」は、 現実の速度ではないことを明らかにしました。 また、 静止している物質の立場に立たなければ、 重力などの物質の間の関係によって決まる物理量については、 正確な観察が不可能であることを示しました。 しかし、 私たちは、 ついつい第3者的な立場で見ようとして、 論理的矛盾( 相対性理論のパラドックス )に陥ってしまいます。 たしかに、 電磁気学では、 マックスウェルの方程式 と ローレンツ変換 により、 電磁場の中で移動している電荷に働く力を正確に観察することが、 一見可能であるかのように思われます。 第3者的な立場で観察することが可能であるかのように思われます。 しかしそれも、 電磁場が空間的時間的に変化する場合には、 電磁場の発生源から移動する電荷に電磁場が伝わるのに要する時間や距離も考慮しなければなりませんので、 電荷が静止している慣性系に座標変換してから考えなければ正確な力を求めることができません。
アインシュタインは、 一般相対性理論の中でも「 みかけ 」を排除して、 観察者自身の当事者の立場から物理学を記載するように試ました。 それは、「 みかけの力 」=「 慣性力 」を「 一様な重力場による重力 」に置き換えたことです。 共に地球に向かって自由落下運動をしているあなたとリンゴを思い浮かべてください。「 あなたの立場からすると、 地球の立場からと違い、 このリンゴには、地球の重力と大きさが同じで向きが反対のみかけの力が働いて、 地球の重力と相殺し、 リンゴはあなたに対して静止している。」とニュートン力学は言いますが、 一般相対性理論は、 そうは言わずに次のように言います。「 あなたが観察している空間には、 地球の重力場と大きさが同じで向きが反対の重力場が生じていて、 それによるリンゴへの重力が地球の重力と相殺し、 リンゴはあなたに対して静止している。」
私が思うには、 アインシュタインは、 さらに、 重力の本源を変速度運動に求め、 変速度運動は空間を圧縮するものであることを導こうとしていたのではないかと思います。 さらにアインシュタインは、 一般相対性理論においても、 特殊相対性理論と同様に、 物理学 を「 空間 」と「 時間 」と「 観察者と被観察者との移動関係 」の3つをパラメーターにして記載しようと試みていたのではないだろうかと思います。
さて前置きが長くなりましたが、 さあこれから、 一般相対性理論の土台となる基礎的な考え方について学んでいくことにしましょう。
追伸 :
この「 変速度系相対性理論の足場 」の中でも、「 慣性系相対性理論の手引き 」で紹介しました「 目・工・田 単位系 」を使用させていただきます。
私の自分勝手な解釈( 勘違い )が所々に出てまいりますので、 鵜呑みにせず、 批判しながらお読みください。
まず、 【 ニュートン力学 】を構築している主な方程式を紹介します。
( 本来ならば、 ベクトル表記しなければならないところですが ・ ・ ・ )。
運動方程式 : 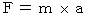
運動量 : 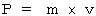
力 : 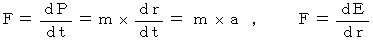 ,
, 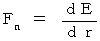
運動エネルギー : 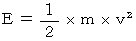
重力 : 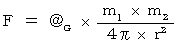
運動エネルギー : 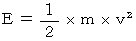 を証明してみましょう。
を証明してみましょう。
 まず、
まず、
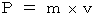
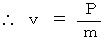
 次に、
次に、
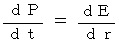
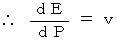
 最後に、
最後に、  と
と  より、
より、
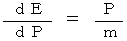
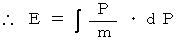
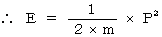
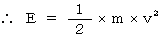
次に、 【 相対論的力学 】を構築している主な方程式を紹介します。
静止質量 : 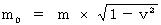
運動方程式 : 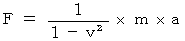
4次元時空間運動量 : 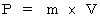
空間運動量 : 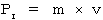
力 : 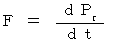 ,
, 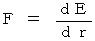
エネルギー : 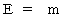
重力 : 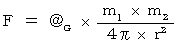
重力は、 重力場( 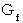 )を用いて次のようにも表されます。
)を用いて次のようにも表されます。
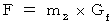 ただし、
ただし、 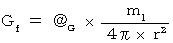
これから、 移動している重力場について考えてみましょう。
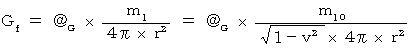
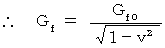
* ただし、 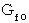 は、 重力場を形成する物質が静止しているとき
は、 重力場を形成する物質が静止しているとき
( 重力場が静止しているとき )の重力場を表します。
私は、 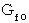 を「 静止重力場 」と言っています。
を「 静止重力場 」と言っています。 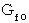 は、 座
は、 座
標変換にて不変です。
この式より、 移動している重力場は静止しているときに比べて 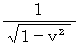 倍 大きくなっていることがわかります。 この関係は、 次のような思考実験によっても裏付けされます。
倍 大きくなっていることがわかります。 この関係は、 次のような思考実験によっても裏付けされます。
「 同じ質量の2つの物質AとBが存在し、 2つを結ぶ線分に対して垂直方向に相対的移動をしている。 今、 物質Aが物質Bに及ぼす重力の大きさについて考える。 物質Aと並走している観察者にとっても物質Bと並走している観察者にとっても、 その大きさは等しくなければならない。 なぜなら、 運動の対称性により、 物質Aと並走している観察者にとっての物質Aが物質Bに及ぼす重力の大きさは、 物質Bと並走している観察者にとっての物質Bが物質Aに及ぼす重力の大きさと等しく、 かつ、 物質Aと並走している観察者にとっての物質Bが物質Aに及ぼす重力の大きさは、 物質Bと並走している観察者にとっての物質Aが物質Bに及ぼす重力の大きさと等しく、 かつ、 作用反作用の法則より、 物質Aと並走している観察者にとっての物質Bが物質Aに及ぼす重力の大きさは、 物質Aと並走している観察者にとっての物質Aが物質Bに及ぼす重力の大きさと等しいからである。
 であるから、 2人の観察者の間で、 物質Aが物質Bに及ぼす重力の大きさが同じになるためには、 物質Bと並走している観察者にとっての物質Bの質量は物質Aと並走している観察者にとっての物質Bの質量に比べて
であるから、 2人の観察者の間で、 物質Aが物質Bに及ぼす重力の大きさが同じになるためには、 物質Bと並走している観察者にとっての物質Bの質量は物質Aと並走している観察者にとっての物質Bの質量に比べて 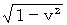 倍になっているため、 物質Bと並走している観察者にとっての重力場は、 物質Aと並走している観察者にとって重力場の
倍になっているため、 物質Bと並走している観察者にとっての重力場は、 物質Aと並走している観察者にとって重力場の 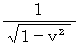 倍 になってなければいけない。 したがって、 速さ
倍 になってなければいけない。 したがって、 速さ  で移動している重力場は、 静止時に比べて
で移動している重力場は、 静止時に比べて 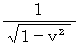 倍の大きさになっている。」
倍の大きさになっている。」
私は、 このことを「 運動する重力場の強化法則 」と言っています。
さて、 ここで、 第1観察者が静止している次の2つの物質の間に働く重力を観察している場合について考えてみましょう。 物質Aと物質Bとの距離は  です。
です。
物質A ( 質量 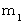 , 静止質量
, 静止質量 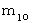 )
)
物質B ( 質量 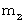 , 静止質量
, 静止質量 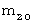 )
)
また、 第2観察者がいて、 2つの物質を結ぶ線分に対して垂直な方向に、 第1観察者に対して速さ  で等速直線運動しています。
で等速直線運動しています。
このとき、 第2観察者にとって物質Aが作る重力場が物質Bに働く重力の大きさは、 次のようになります。
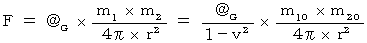
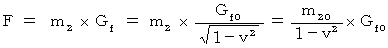
これらの式より、 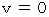 のときが第1観察者にとっての重力になるので、 第2観察者にとっての重力は、 第1観察者にとっての重力に比べて
のときが第1観察者にとっての重力になるので、 第2観察者にとっての重力は、 第1観察者にとっての重力に比べて 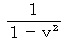 倍 大きいことがわかります。
倍 大きいことがわかります。
この重力によって物質Bは加速的変速度運動を開始するのですが、 第2観察者にとってのその変速度の大きさ(  )は、 次のようになります。
)は、 次のようになります。
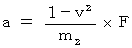 と
と 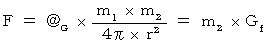 より、
より、
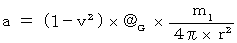 または、
または、 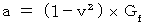
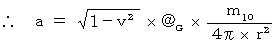 または、
または、 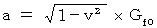
これらの式より、 第2観察者にとっての加速度は、 第1観察者にとっての加速度に比べて 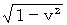 倍 小さいことがわかります。
倍 小さいことがわかります。
以上のように、 座標変換によって、 物質Bに働く力や物質Bの変速度が変化しています。 はたして、 これで相対性原理が成り立っていると言えるのでしょうか? これに対して次のような考え方があると思います。
 2つの座標系で共に運動方程式が成り立っているから、相対性原理は成立している。その上、実験で、高速で移動する粒子は重力による変速度が小さくなるというデーターが存在するので、間違いない。
2つの座標系で共に運動方程式が成り立っているから、相対性原理は成立している。その上、実験で、高速で移動する粒子は重力による変速度が小さくなるというデーターが存在するので、間違いない。
 物質Bに対して第3者的観察をしている第2観察者の観察内容は確かなものではなく、 当事者の立場に立っている第1観察者の観察内容こそ真実である。
物質Bに対して第3者的観察をしている第2観察者の観察内容は確かなものではなく、 当事者の立場に立っている第1観察者の観察内容こそ真実である。
どちらが正しいのか、 今の私にはわかりません。
次に、 運動方程式がニュートン力学と異なっているところに注目してください。 相対論的力学では、 力の大きさが、 ニュートン力学に比べて 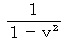 倍 になっています。( 目・工・田 単位系です。)その理由は次の2つです。
倍 になっています。( 目・工・田 単位系です。)その理由は次の2つです。
 力の定義は、 運動方程式であり、 それから導かれる次の「 運動量原理 」と「 エネル
力の定義は、 運動方程式であり、 それから導かれる次の「 運動量原理 」と「 エネル
ギー原理 」である。
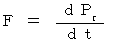
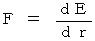
 相対論的力学では、 物質が加速的または減速的変速度運動をしているときには、 質量は時間とともに変化する。
相対論的力学では、 物質が加速的または減速的変速度運動をしているときには、 質量は時間とともに変化する。
今から、このことを、式を用いて説明します。
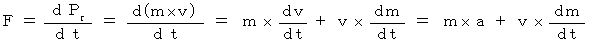
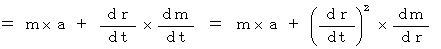
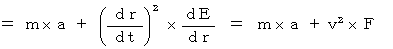
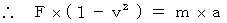 ・ ・ ・ ・( 式 01-01 )
・ ・ ・ ・( 式 01-01 )
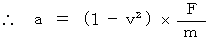 ・ ・ ・ ・( 式 01-02 )
・ ・ ・ ・( 式 01-02 )
* 私は、( 式 01-02 )を、「 相対論的変速度方程式 」と言っています。
さて、 エネルギーの概念は、 相対論的力学では次のようになります。
「 位置的エネルギーを除外して考えるとき、 物質の持つエネルギーは、 その物質の質量で表わされる。 物質の持つエネルギーは、 静止質量 m 0( 核結合エネルギー や 熱エネルギー や 化学エネルギー などを含んでいる。)と 相対論的運動エネルギー( m − m 0 )とを含んでいる。 物質の空間移動の速さが光に比べてはるかに遅い時は、 物質の持つエネルギーは、 およそ、 静止質量 と ニュートン力学的運動エネルギー の和に等しい。」
「 物質の空間移動の速さが光に比べてはるかに遅い時は、 物質の持つエネルギーは、 およそ、 静止質量 と ニュートン力学的運動エネルギー の和に等しい。」とはどういう意味なのか、 それは、 次のマクローリン展開式 を見ると理解できます。
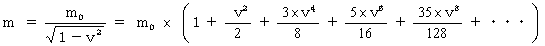
この式は、 v が 0 に近いとき、 第3項以降は 0 に近くなりますので、 次のようになります。
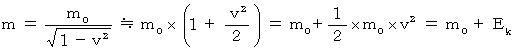
つまり、 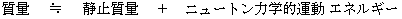 になります。
になります。
相対論的力学では、 一般的には、 質量 と 静止質量 の関係は、 次の式で表わされます。
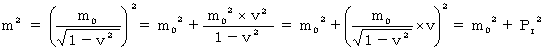
つまり、 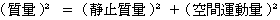 です。
です。
これは、 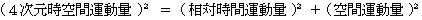 と同義です。
と同義です。
つまり、 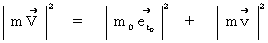 と同義です。
と同義です。
相対性理論では、 エネルギーは大きく2つに分けられます。 それは「 質量的エネルギー 」と「 位置的エネルギー 」です。
総エネルギー 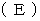 = 質量的エネルギー + 位置的エネルギー
= 質量的エネルギー + 位置的エネルギー
質量的エネルギー = 静止質量エネルギー + 相対論的運動エネルギー
* 質量的エネルギー = 質量
* 静止質量エネルギー = 静止質量
総エネルギー 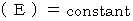 のことを、「 エネルギー保存の法則 」と言います。
のことを、「 エネルギー保存の法則 」と言います。
位置的エネルギー と 相対論的運動エネルギーとを合わせて、「 力学的エネルギー 」と言います。 位置的エネルギー と 相対論的運動エネルギー は相互に変換されますが、 これらは、 普通は、 静止質量エネルギーには変換されません。
 の角振動数の光は、質量的エネルギー
の角振動数の光は、質量的エネルギー 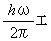 を持っています。 すべての光の静止質量エネルギーは
を持っています。 すべての光の静止質量エネルギーは 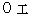 ですので、 角振動数
ですので、 角振動数  の光は、
の光は、 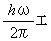 の相対論的運動エネルギーを持っていることになります。
の相対論的運動エネルギーを持っていることになります。
* 工 は、 質量の単位です。
質量的エネルギー = 質量 ですから、 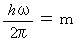 です。
です。
* コメント:
 光の場合は、 静止質量が 0 なので、質量は 0 であると思いがち
光の場合は、 静止質量が 0 なので、質量は 0 であると思いがち
ですが、 よく考えるとそれは違います。
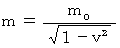 に
に 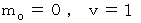 を代入してみてください。
を代入してみてください。
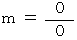 になります。
になります。 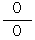 は 0 とは限りません。
は 0 とは限りません。
 光の静止質量は
光の静止質量は 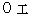 だけれども、 光の質量的エネルギーは
だけれども、 光の質量的エネルギーは 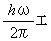
であるので、「 光は重力( 質量間力 )の影響を受け、 それはあたかも
質量 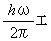 の物質のようである。」と考えても、 便宜上問題ありません。
の物質のようである。」と考えても、 便宜上問題ありません。
このことの本当の意味については、 第3章で勉強しましょう。
光が重力場の向きと反対方向に伝わってきたとき、「 力学的エネルギー保存の法則 」によって、 相対論的運動エネルギーの一部が位置的エネルギーに変換されるため、 そのぶんだけ角振動数が減少します。 ということは、 重力場に抗して伝わってきた光は、 振動数が小さくなって波長が伸びます。 これを「 重力赤方偏移 」と言います。
「 重力赤方偏移 」は、「 横ドップラー効果 」と同様に、「 電磁波や量子が放たれている空点の時間の経過が遅れていることの証拠である。」と言われます。 このことに関しては、 第8章で述べたいと思います。
次のページへ 目次に戻る
 ばいおりんのその他の相対論関連論文集 に戻る
ばいおりんのその他の相対論関連論文集 に戻る ばいおりんの慣性系相対性理論 に行く
ばいおりんの慣性系相対性理論 に行く ホームページのトップへ 戻る
ホームページのトップへ 戻る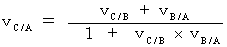
 で等速直線運動している第1観察者の慣性系へと座標変換されると、 どんな変化が起こるのか述べます。
で等速直線運動している第1観察者の慣性系へと座標変換されると、 どんな変化が起こるのか述べます。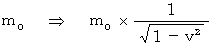

 )
)
 の絶対時間に 物質が移動する 相対時間
の絶対時間に 物質が移動する 相対時間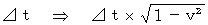

 の絶対時間に 物質が移動する 空間
の絶対時間に 物質が移動する 空間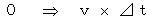
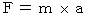
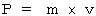
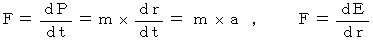 ,
, 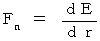
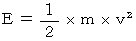
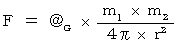
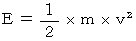 を証明してみましょう。
を証明してみましょう。 まず、
まず、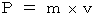
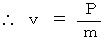
 次に、
次に、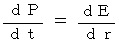
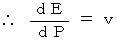
 最後に、
最後に、  と
と  より、
より、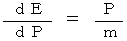
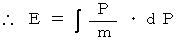
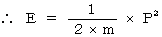
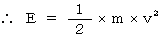
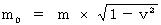
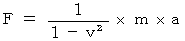
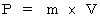
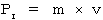
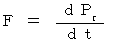 ,
, 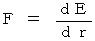
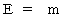
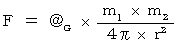
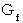 )を用いて次のようにも表されます。
)を用いて次のようにも表されます。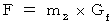 ただし、
ただし、 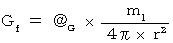
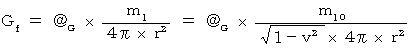
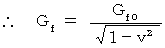
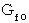 は、 重力場を形成する物質が静止しているとき
は、 重力場を形成する物質が静止しているとき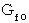 を「 静止重力場 」と言っています。
を「 静止重力場 」と言っています。 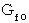 は、 座
は、 座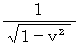 倍 大きくなっていることがわかります。 この関係は、 次のような思考実験によっても裏付けされます。
倍 大きくなっていることがわかります。 この関係は、 次のような思考実験によっても裏付けされます。 であるから、 2人の観察者の間で、 物質Aが物質Bに及ぼす重力の大きさが同じになるためには、 物質Bと並走している観察者にとっての物質Bの質量は物質Aと並走している観察者にとっての物質Bの質量に比べて
であるから、 2人の観察者の間で、 物質Aが物質Bに及ぼす重力の大きさが同じになるためには、 物質Bと並走している観察者にとっての物質Bの質量は物質Aと並走している観察者にとっての物質Bの質量に比べて 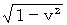 倍になっているため、 物質Bと並走している観察者にとっての重力場は、 物質Aと並走している観察者にとって重力場の
倍になっているため、 物質Bと並走している観察者にとっての重力場は、 物質Aと並走している観察者にとって重力場の 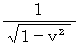 倍 になってなければいけない。 したがって、 速さ
倍 になってなければいけない。 したがって、 速さ  で移動している重力場は、 静止時に比べて
で移動している重力場は、 静止時に比べて 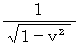 倍の大きさになっている。」
倍の大きさになっている。」 です。
です。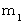 , 静止質量
, 静止質量 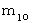 )
)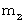 , 静止質量
, 静止質量 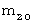 )
) で等速直線運動しています。
で等速直線運動しています。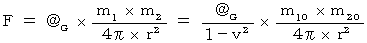
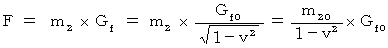
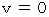 のときが第1観察者にとっての重力になるので、 第2観察者にとっての重力は、 第1観察者にとっての重力に比べて
のときが第1観察者にとっての重力になるので、 第2観察者にとっての重力は、 第1観察者にとっての重力に比べて 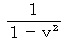 倍 大きいことがわかります。
倍 大きいことがわかります。 )は、 次のようになります。
)は、 次のようになります。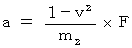 と
と 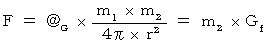 より、
より、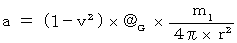 または、
または、 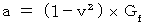
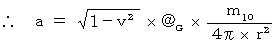 または、
または、 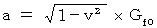
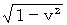 倍 小さいことがわかります。
倍 小さいことがわかります。 2つの座標系で共に運動方程式が成り立っているから、相対性原理は成立している。その上、実験で、高速で移動する粒子は重力による変速度が小さくなるというデーターが存在するので、間違いない。
2つの座標系で共に運動方程式が成り立っているから、相対性原理は成立している。その上、実験で、高速で移動する粒子は重力による変速度が小さくなるというデーターが存在するので、間違いない。 物質Bに対して第3者的観察をしている第2観察者の観察内容は確かなものではなく、 当事者の立場に立っている第1観察者の観察内容こそ真実である。
物質Bに対して第3者的観察をしている第2観察者の観察内容は確かなものではなく、 当事者の立場に立っている第1観察者の観察内容こそ真実である。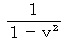 倍 になっています。( 目・工・田 単位系です。)その理由は次の2つです。
倍 になっています。( 目・工・田 単位系です。)その理由は次の2つです。 力の定義は、 運動方程式であり、 それから導かれる次の「 運動量原理 」と「 エネル
力の定義は、 運動方程式であり、 それから導かれる次の「 運動量原理 」と「 エネル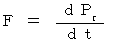
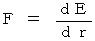
 相対論的力学では、 物質が加速的または減速的変速度運動をしているときには、 質量は時間とともに変化する。
相対論的力学では、 物質が加速的または減速的変速度運動をしているときには、 質量は時間とともに変化する。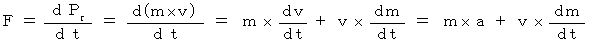
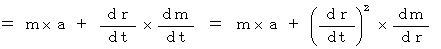
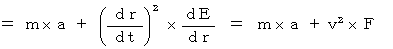
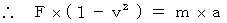 ・ ・ ・ ・( 式 01-01 )
・ ・ ・ ・( 式 01-01 )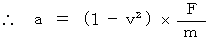 ・ ・ ・ ・( 式 01-02 )
・ ・ ・ ・( 式 01-02 )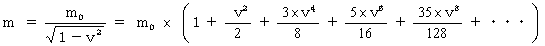
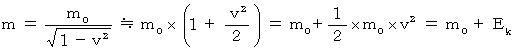
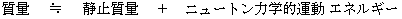 になります。
になります。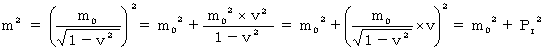
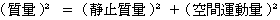 です。
です。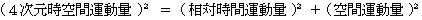 と同義です。
と同義です。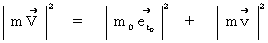 と同義です。
と同義です。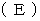 = 質量的エネルギー + 位置的エネルギー
= 質量的エネルギー + 位置的エネルギー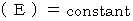 のことを、「 エネルギー保存の法則 」と言います。
のことを、「 エネルギー保存の法則 」と言います。 の角振動数の光は、質量的エネルギー
の角振動数の光は、質量的エネルギー 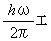 を持っています。 すべての光の静止質量エネルギーは
を持っています。 すべての光の静止質量エネルギーは 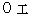 ですので、 角振動数
ですので、 角振動数  の光は、
の光は、 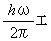 の相対論的運動エネルギーを持っていることになります。
の相対論的運動エネルギーを持っていることになります。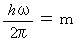 です。
です。 光の場合は、 静止質量が 0 なので、質量は 0 であると思いがち
光の場合は、 静止質量が 0 なので、質量は 0 であると思いがち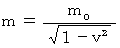 に
に 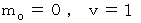 を代入してみてください。
を代入してみてください。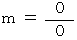 になります。
になります。 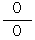 は 0 とは限りません。
は 0 とは限りません。 光の静止質量は
光の静止質量は 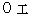 だけれども、 光の質量的エネルギーは
だけれども、 光の質量的エネルギーは 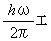
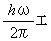 の物質のようである。」と考えても、 便宜上問題ありません。
の物質のようである。」と考えても、 便宜上問題ありません。