第4章 慣性 と 慣性力
(1)慣性とは何か
-
無重力宇宙空間を等速直線運動しているロケットの中は、 無重力状態です。 ここでロケットエンジンをかけてロケットを加速的変速度運動させると、 ロケットの中の物質には、「 重力 」のような、 物質の質量に比例する力が働くようになります。 こういう「 みかけの力 」は「 慣性力 」と言われます。「 慣性力 」は、「 慣性 」そのものではありません。 また、「 慣性の法則 」によって生み出される力でもありません。「 慣性 」や「 慣性の法則 」と紛らわしくなるだけなので、 私は「 慣性力 」という言葉は使わずに「 相対的変速度力 」と言っています。
「 相対的変速度力 」とは何かを明らかにするため、 まず、「 慣性 」とは何かを考えてみたいと思います。
「 慣性 」 とは、 元来は「 慣性の法則 」が意味するものでした。 つまり、 ニュートンの運動方程式 :
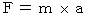 より、
より、 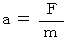 であり、
であり、 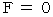 のとき
のとき 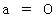 ですから、「 物質に力が加わらなければ、 物質は等速直線運動( 静止を含む )を続ける。 この物質の性質を、 慣性という。」というのが、 元々の「 慣性 」の意味です。
ですから、「 物質に力が加わらなければ、 物質は等速直線運動( 静止を含む )を続ける。 この物質の性質を、 慣性という。」というのが、 元々の「 慣性 」の意味です。* コメント : ニュートンの運動の第1法則 : 慣性の法則
ニュートンの運動の第2法則 : 運動方程式
ニュートンの運動の第3法則 : 作用・反作用
それが、「 力に対抗して変速度を大きくしないようにしている質量 」が「 慣性 」を表す、 という考え方に発展してきました。 そして、「 慣性質量 」という物理学用語ができました。 私は、 後者の「 慣性 」の概念を、 元来の「 慣性 」の概念と区別するために、「 慣性度 」という言葉を使っています。「 慣性度 」とは、 いわば、「 静止している物質を移動させようとした時の、 移動のさせにくさ 」です。
質量が「 慣性度 」を担っているわけですが、 ここで1つ注意しなければならないことがあります。 それは、 次のように考えてしまうことです。
「 質量が 1 工 未満のときは、 質量は変速度を大きくするようにふるまう。 これは、 慣性の逆だ。 したがって、 1 工 よりも大きい質量のみが慣性を担うのだ。 すると、 単位系によって、 同じ量の質量が、 慣性を担ったり、 慣性を妨げたりする。 おかしい!? 」
* コメント : 工 は、「 目・工・田 単位系 」の質量の単位です。
そこで、「 慣性度 」を次のように定義します。
まず、( 式 01-02 ):「 相対論的変速度方程式 」 と ( 式 01-03 )より、 次の式が成り立つことを先に提示しておきます。
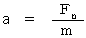 ・ ・ ・ ・( 式 04-01 )
・ ・ ・ ・( 式 04-01 )「 慣性度とは、 変速度を 1 目−1 にするために、 その時点で必要と見積もられるニュートン力学的力の大きさである。 それは、 ちょうど質量に等しいので、 慣性度は質量に等しいと言える。 しかし、 慣性度の単位は、 力の単位であって、 質量の単位ではない。」
この定義からすると、 質量が 1 工 未満であったとしても矛盾しないことがわかります。
また、「 その時点で必要と見積もられる 」という言葉が入っている意味は、 次のようなものです。
「 変速度 1 目−1 を達成するためには、 物質の速さを増大させなければなりません。 物質の速さが増大すると、 物質の質量は増大します。 すると、 初期に見積もられていたよりも大きな力を加えなければ、 変速度 1 目−1 を達成することができなくなり、 修正が必要になります。 そうして、 この作業が無限に続くことになります。」
「 運動方程式 」の中では、 質量は慣性を担う物として取り扱われ、「 慣性質量 」と言われます。 一方、「 万有引力の法則 」の中では、 質量は重力( 重さ )を担う物として取り扱われ、「 重力質量 」と言われます。 そして、 重力場によって生じる物質の変速度と重力場の間には、 次のような関係があります。
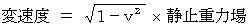
この式は次の3つの式から導かれます。
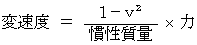
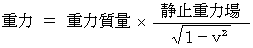
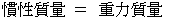
しかし、 実際は「 慣性質量 」と「 重力質量 」の2種類の質量が存在するわけではなく、 実在するのは「 質量 」だけなので、「 慣性質量 」とか「 重力質量 」という物理学的用語は無いほうがいいと、 私は考えています。
-
「 相対的変速度力( 慣性力 )とは、 変速度運動をする箱の中に生じる一様な重力場による重力である。」ということができます。 たとえば、 飛行機が離陸する時、 飛行機の前方にもう一つの天が生じて、 乗客はシートの背もたれに寝転ぶようになりますが、 これは乗客に新たな重力がかかると同時に背もたれから抗力がかかっている状態です。 もし、飛行機の床にボールがあったとすれば、 ボールは重力によって進行方向と逆に自由落下のような変速度運動をします。
電車の中にいる観察者にとっては、 等速直線運動をしている電車も、 静止している電車も変わりありません。 等速直線運動をしている電車とは、 電車に対して等速直線運動している電車の外の観察者が観察した場合の電車のことで、 静止している電車とは、 電車に対して静止している電車の外の観察者が観察した場合の電車のことです。 電車の中にいる観察者にとっては、 駅から出発するときの電車は静から動で、 駅に到着するときの電車は動から静ではありません。 両方とも静から動です。 電車が加速し始めてからも元の電車と同じ速度で移動する観察者にとって、 前者は電車の変速度が電車の後部から前部を向かう方向であり、 後者は電車の変速度が電車の前部から後部を向かう方向です。 このことは、 電車の中にいる観察者にとっても同じことです。 したがって、 電車の中にいる観察者に作用する相対的変速度力( 慣性力 )は、 前者は電車の前部から後部を向かう方向で、 後者は電車の前部から後部を向かう方向です。 電車の変速度の大きさを a目−1 とすると、 質量 m 工 の電車の中に存在する物質に対して作用する相対的変速度力( 慣性力 )は、 −am 目−1 です。
-
先ほどは、 観察者の入っている箱が変速度運動をした場合を考えましたが、 今度は観察者自身が変速度運動をする場合を考えましょう。 観察者は重力場の中で目の前の物質と共に自由落下しています。 観察者の観察している物質は今無重力空間にある物質であると言えます。 ここで、 観察者は背負ったロケットエンジンを噴射させて重力と吊りあう力を出しました。 すると観察者は変速運動から等速運動に変わります。 そして観察者の観察する物質は静止から加速的直線的変速度運動に変わります。 このとき、 観察者にとっては、「 自分は無重力空間の中にいて、 途中から加速的直線的変速度運動をしたので、 物質には 相対的変速度力( 慣性力 )が働き、 加速的直線的変速度運動を開始した。」ということになります。 このように、 観察者にとっては、 無重力空間で重力を作ったということになるのですが、 それを客観的に見ている私たちにとっては、 観察者は重力空間の中で自分だけの重力を消したということになります。
このように、 座標変換( 観察者 と 被観察物質 との運動関係 )によって、「 重力 」は、 消失したり、 出現したりします。
第5章 重力場も相対的なものである。
まず、 等速円運動の相対性について考えましょう。 等速円運動も変速度運動の1種です。
思い浮かべてください。 今、 B君 がA君の東側にいて、 向かい合っています。 次に、 B君は西を向いたままA君の周りを反時計回りに1回転します。 この現象は、 B君の立場からすると、 自分が静止していてA君が自分の周りを反時計回りに1回転したことになるのではないでしょうか。「 でも、 エネルギーを使ったのはB君のほうだし、 A君がB君の周りを回転したとは考えられない。」という人は、 A君 と B君 はお互いに2人の間に働く重力によって等速円運動していると思ってください。
すると、 はっと気付きます。「 太陽は地球の影響を受けて回転運動をしているのです。 ただし、 地球の自転による見かけの太陽の周回のことを言っているのではありません。 地球が太陽の周りを1公転する間( 1年間 )に、 太陽は小さな円運動を1回行っているのです。 太陽と地球とでは質量が33万倍も違いますので、 地球と太陽との間での重力に限ってい言えば、 地球の重心が存在する空点の太陽による重力場は、 太陽の重心が存在する空点の地球による重力場の33万倍の大きさになっているのです。 加速度 = 重力場 ですから、 地球は、 太陽に比べて33万倍の大きさの加速度運動をしていることがわかります。 もし、 質量が等しい天体がお互いの重力により円軌道上を公転し合うのであれば、 それを客観的に観察している人からすると、 2つの天体の重心を結ぶ線分の中点を中心にして、 お互いが同じ円軌道をπの角度を保ったまま等速円運動することになります。
次に、 落下運動について考えてみましょう。 2つの物質間の重力によるそれぞれの物質の落下運動は、 一般的には、 それぞれ相手の物質の位置を焦点の1つとする楕円運動です。 それに含まれる両極端が、 等速円運動 と 単振動 です。
これから、2つの物質間の重力によるそれぞれの物質の単振動について考えてみましょう。 地球に穴を掘り、地球の重心を通って地球の裏側まで落下できるような環境を作ります。 その穴に飛び降りると、 単振動が始まります。 落下運動している人の立場からすると、「 自分は無重力状態で、 地球が自分を中心にして単振動している。」ということになります。
ただし、 ここに1つ矛盾点があります。 落下運動している人はこう思うでしょう。
「 地球の変速度はあまりにも大きすぎる。 地球が運動しているのは、 自分が作っている重力場によるはずだ。 私が作る重力場は小さいので、 変速度 = 重力場 からすると、 こんなに大きな変速度が生じるわけはない。」
実を言うと、 落下中の人にとっては、 自分の存在する空点に重力場は存在しませんが、 地球の重心が存在する空点には「 自分が地球の重心が存在する空点に作り出している重力場 」から「 地球が自分の存在する空点に作り出している重力場 」をベクトル的に引いた重力場が存在しているのです。
つまり、 落下中観察者からすると、 全空間に、 自分が存在する空点の重力場と大きさが等しくて向きが逆の重力場が存在しており、 自分の存在する空点は、 その重力場と元来の重力場が相殺しあって 0 になっているのです。
私は、「 無重力空間で変速度運動をしている観察者の座標系のすべての空点に存在する、 その変速度と大きさが等しくて向きが逆の一様な重力場 」のことを、「 相対的一様重力場 」と言っています。「 相対的一様重力場 」は実在の重力とベクトル合成することができ、 ベクトル合成された重力場が、 観察者の座標系の実際の重力場になります。
追伸 :
-
第3者的な見方をすれば、 重力場が存在していますが、 落下運動をしている物質の立場に立てば、 重力場は存在しません。 ということは、 座標変換により、 力が消失したことになります。 これは、「 どんな座標系においても、 物質の物理学的な現象については、 同じ物理学的法則が成立する。」という一般相対性原理に背くことになりはしなでしょうか? でもその心配はありません。「 同じ物理学的法則が成立する。」ということは、「 物質の移動の形態 」のことを言っているのではなく、「 力学的あるいは電磁気学的な方程式 」のことを言っているからです。 座標変換によって、 力が 0 になろうとも、 ニュートンの運動方程式が成立しておれば、 それでよいのです。