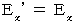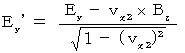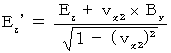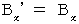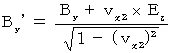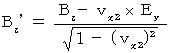(5) Interpretation of Maxwell's equations
The standard Maxwell's equations are as follows :

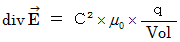

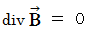

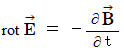

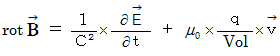
 be volume.
be volume.
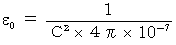
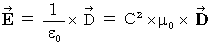
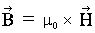
Maxwell's equations are shown as follows with substantial electric field; substantial electric field is obtained by dividing electric field by speed of light :

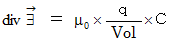

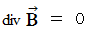

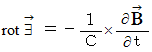

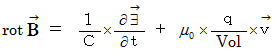
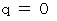 , these equations are expressed as
, these equations are expressed as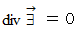
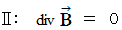
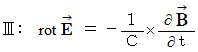
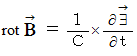
 , and then we apply the
, and then we apply the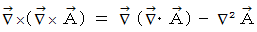 , and then
, and then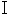 and the equation
and the equation 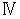 as
as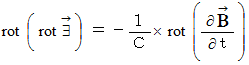
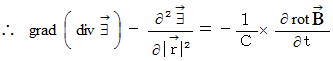
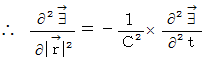
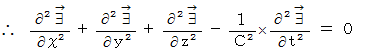
Maxwell's equations are shown as follows with
 system of units :
system of units :
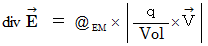

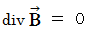

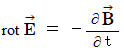

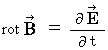
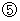
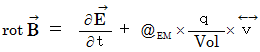
 be volume.
be volume.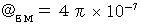
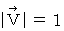
Each equations means as follows :




(6) Four-dimensional electromagnetic potential and basic equations of electomagnetics
Now, I show some theorems on the electromagnetic potential as follows :









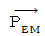 ).'
).' Maxwell's equations are expressed with electric potential
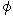 and electric current potential
and electric current potential 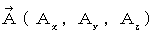 as follows :
as follows :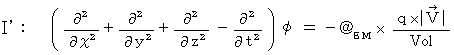
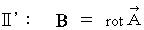
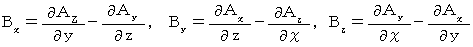
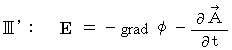
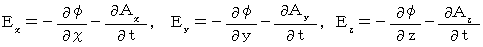
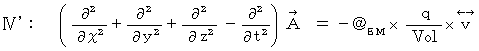

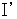 with
with 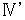 , we obtain the following equality :
, we obtain the following equality : 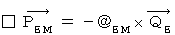
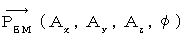
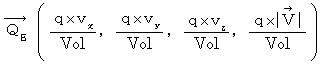
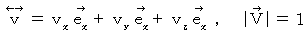
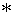
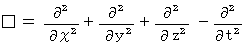
 ).
).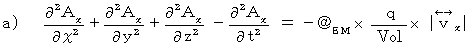
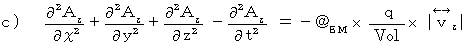
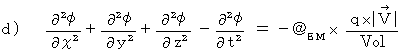
On the condition of
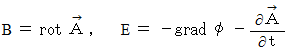 , when
, when 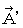 obtained with the vector function
obtained with the vector function 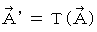 and
and 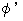 obtained with the scalar function of
obtained with the scalar function of 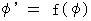 make the following equality be satisfied,
make the following equality be satisfied,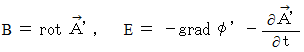
we say as follows :
 The vector function
The vector function 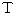 and the scalar function
and the scalar function 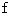 are gauge transformations.
are gauge transformations.
Let
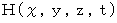 be an optional scalar function. There are the vector function
be an optional scalar function. There are the vector function 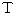 and the scalar function
and the scalar function 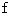 as follows :
as follows :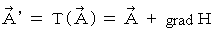
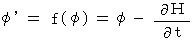
When we replace
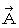 and
and 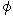 with
with 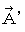 and
and 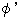 respectively,
respectively, 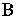 and
and 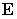 don't change as follows :
don't change as follows :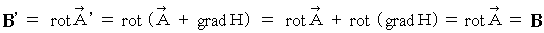
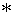 We use the formula :
We use the formula :  .
.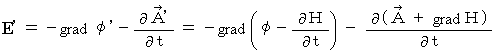
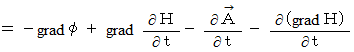
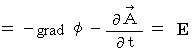
Therefore,
 and
and  are gauge transformations.
are gauge transformations.Now, I explain why Maxwell's equations are shown as
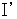
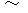
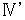 .
.First, I show Maxwell's equations again as follows :
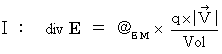
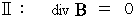
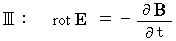
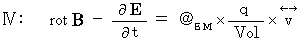
Let
 be 'electric current potential'. We suppose that the following equality is satisfied :
be 'electric current potential'. We suppose that the following equality is satisfied :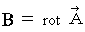
 (Equality 22-12)
(Equality 22-12)Then, we obtain the following equality owing to the equation
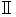 :
: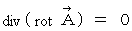
This equality meets the theorem of vector analysis :
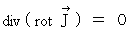 .
.And, there is the theorem of vector analysis as follows :
 If it is
If it is 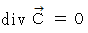 ,
, 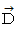 , which makes the equality :
, which makes the equality : 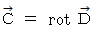 be satisfied, is sure to exist.
be satisfied, is sure to exist.
Therefore, we know (Equality 22-12) is equivalent to the equation
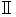 .
.Owing to the equality
 and (Equality 22-12), we obtain the following equation :
and (Equality 22-12), we obtain the following equation :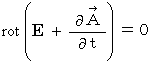
Therefore, owing to the formula :
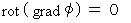 , we obtain the following equation :
, we obtain the following equation :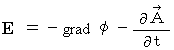

Owing to the formula of electromagnetism :
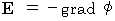 ,we know that
,we know that 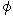 of (Equality 22-13) is electric potential. Then, we know as follows :
of (Equality 22-13) is electric potential. Then, we know as follows : Electric field is produced not only by gradient of electric potential but also by the change of 'electric current potential.'
Electric field is produced not only by gradient of electric potential but also by the change of 'electric current potential.'
I have described that 'the replacement of
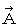 and
and 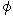 of (Equality 22-12) and (Equality 22-13) with
of (Equality 22-12) and (Equality 22-13) with 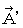 obtained with
obtained with 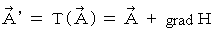 and
and 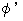 obtained with
obtained with 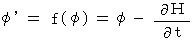 , respectively' does not change
, respectively' does not change 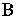 and
and 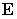 .
. The Maxwell's equations
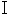 and
and 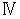 are described with
are described with 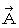 and
and 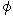 as follows :
as follows :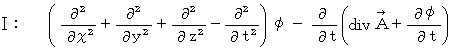
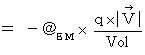

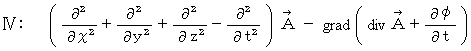
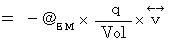

We find the equation
 with the following method :
with the following method :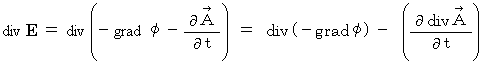
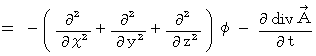
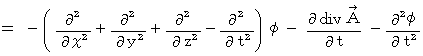
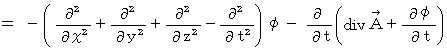
We find the equation
 with the following method :
with the following method :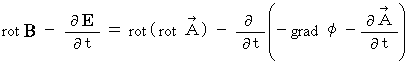
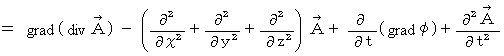
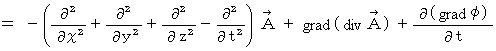
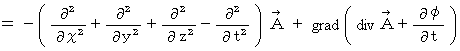
If
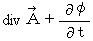 is equal to
is equal to  , the form of (Equality 22-11) comes to look like the form of (Equality 22-14).
, the form of (Equality 22-11) comes to look like the form of (Equality 22-14).So, let us think about
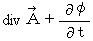 .
.It is
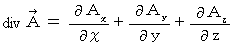 .
.We consider the four-dimensional vector
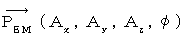 .
.Then,
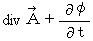 is shown as follows :
is shown as follows :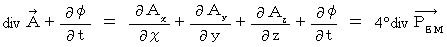
The four-dimensional vector
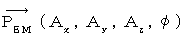 is called 'four-dimensional electromagnetic potential.' It is a four-dimensional vector made up of vector potential of magnetic field and scalar potential of electric field.
is called 'four-dimensional electromagnetic potential.' It is a four-dimensional vector made up of vector potential of magnetic field and scalar potential of electric field.We suppose that it is
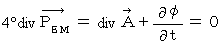 .
.Then, 'Maxwell's equations expressed with electromagnetic potential' of (Equality 22-11)
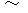 (Equality 22-14) is shown as follows :
(Equality 22-14) is shown as follows :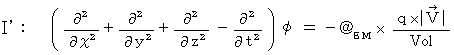
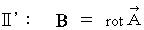
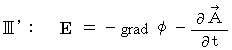
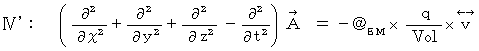
We collect
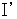 and
and 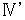 into the following equation :
into the following equation :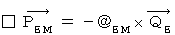
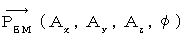
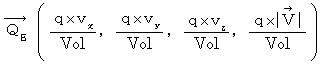
Now, let us find whether the hypothesis :
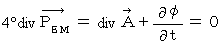 has contradiction.
has contradiction.Owing to the basic equations of electromagnetics with non-spring four-dimensional electromagnetic potential :
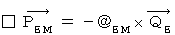 , we obtain the following equality :
, we obtain the following equality :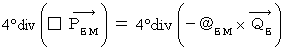
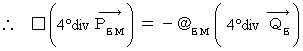

Owing to the Maxwell's equation
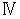 , we obtain the following equation :
, we obtain the following equation :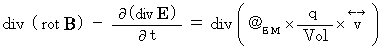
Plugging the theorem:
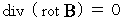 and the Maxwell's equation
and the Maxwell's equation 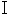 into this equation, we obtain the following equation :
into this equation, we obtain the following equation :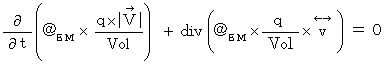
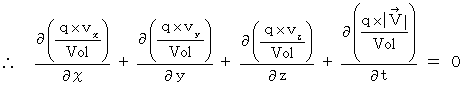
Setting
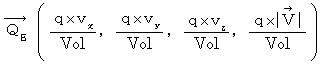
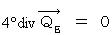

This equation is generally called 'principle of conversation of charge.' I, however, call it 'law of non-spring four-dimensional amount of electric charge density.' Plus, I call
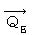 'four-dimensional amount of electric charge density.'
'four-dimensional amount of electric charge density.'Plugging (Equality 22-16) into (Equality 22-15), we obtain the following equation :
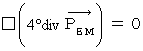
Now, let us find whether the left-hand side of this equality is actually
 .
.
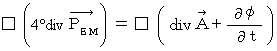
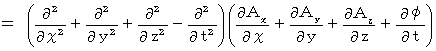
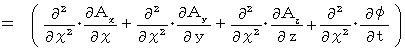
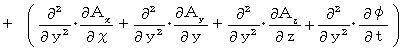
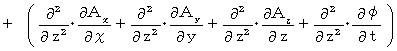
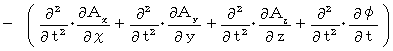
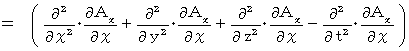
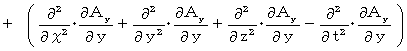
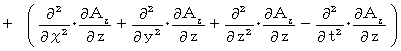
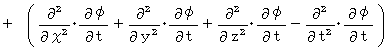

Differentiating both sides of X-component with respect to
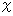 , we obtain the following equation :
, we obtain the following equation :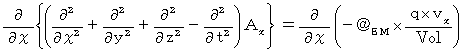
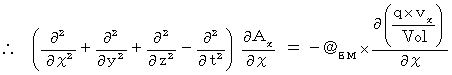
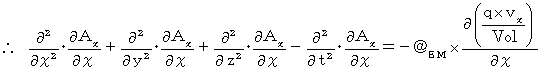
Differentiating both sides of Y-component with respect to
 , we obtain the following equation :
, we obtain the following equation :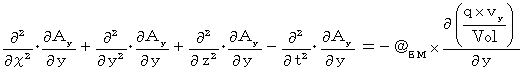
Differentiating both sides of Z-component with respect to
 , we obtain the following equation :
, we obtain the following equation :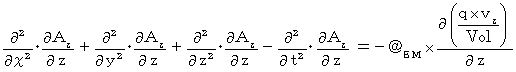
Differentiating both sides of T-component with respect to
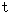 , we obtain the following equation :
, we obtain the following equation :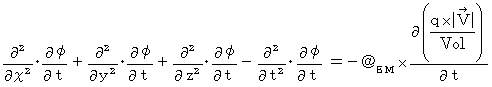

 .
.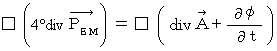
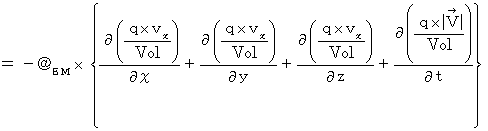
We plug the following 'law of non-spring of four-dimensional amount of electric charge density' into the above-mentioned equation :
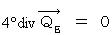
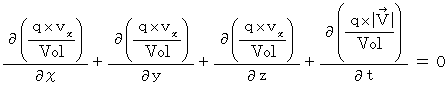
Then, we obtain the following equation:
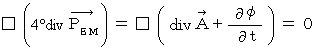
That's why, the hypothesis :
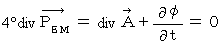 has no contradiction. Therefore, we accept this equation. This equation is called 'Lorenz condition' or 'Lorenz gauge.' I, however, call it 'condition of non-spring four-dimensional electromagnetic potential.'
has no contradiction. Therefore, we accept this equation. This equation is called 'Lorenz condition' or 'Lorenz gauge.' I, however, call it 'condition of non-spring four-dimensional electromagnetic potential.'Is there certainly the electromagnetic potential
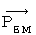 which meets the Lorenz condition? Is there certainly a combination of
which meets the Lorenz condition? Is there certainly a combination of 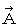 and
and 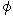 which meets the Lorenz condition?
which meets the Lorenz condition?First, we suppose that it is
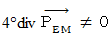 .
.Then, we gauge-transform a combination of
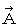 and
and 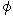 as follows :
as follows :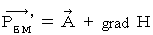 ,
,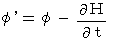
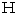 is an optional scalar function.
is an optional scalar function.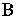 and
and 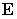 never change.
never change.Second, we find the diversion of four-dimensional electromagnetic potential
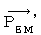 made up of
made up of 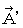 and
and 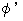 as follows :
as follows :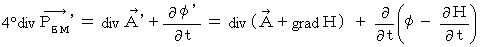
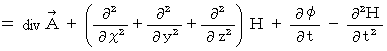
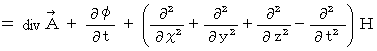
We can choose the function
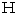 which makes the following equation be satisfied, because it is an optional function :
which makes the following equation be satisfied, because it is an optional function :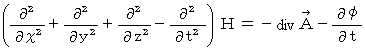
Then,
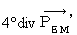 certainly becomes
certainly becomes  .
.That's why, we know that there is certainly the electromagnetic potential
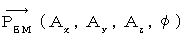 which meets the Lorenz condition.
which meets the Lorenz condition.'Basic equations of electromagnetics with non-spring electromagnetic potential' are constant regardless of Lorentz transformation, because Lorentz transformation was found so that Maxwell's equation is constant regardless of coordinate conversion.
In space in which no amount of electric charge exists, 'Basic equations of electromagnetics with non-spring four-dimensional electromagnetic potential' is a wave equation.
(7) The origin of complex number electromagnetic field tensor
I described that Maxwell's equations are expressed with four equations with scalar potential of electric field, i.e. electric potential (
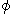 ), and vector potential of magnetic field
), and vector potential of magnetic field 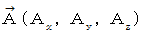 .
. We think with the following two of these equalities; these two equalities correspond to [ Equation
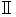 ] and [ Equation
] and [ Equation  ] of Maxwell's equations :
] of Maxwell's equations :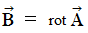
 (Equality 2271)
(Equality 2271)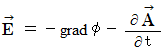
 (Equality 2272)
(Equality 2272)Firstly, (Equality 2271) is expressed as follows :
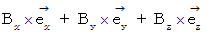
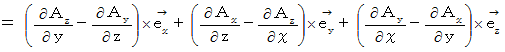
Therefore, we obtain the following equality :
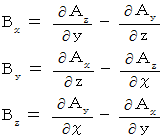
We set as follows :
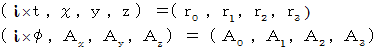
 Complex number four-dimensional electromagnetic potential
Complex number four-dimensional electromagnetic potential is expressed as follows :
is expressed as follows :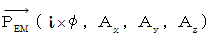
We set the following second-order tensor :
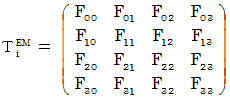
We st as follows :
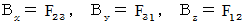
Then, we obtain the following equality :
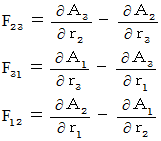
Therefore, we find that these three equalities belong to the following equality :
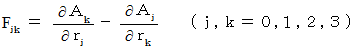
 (Equation 2273)
(Equation 2273)Well, owing to (Equation 2273), we obtain the following equality :
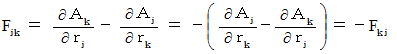
Secondly, (Equation 2272) :
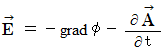 is expressed as follows :
is expressed as follows :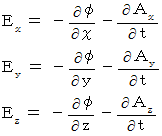
We set as follows :
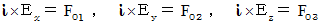
Then, we obtain the following equality :
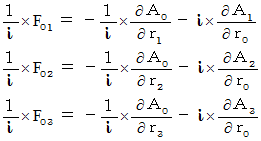
These three equalities becomes as follows :
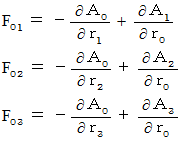
Therefore, these three equalities are expressed as follows :
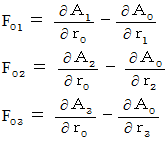
We can integrate these three equalities into the following one :
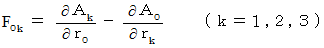
This equality belongs to (Equality 2273) :
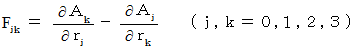 .
.Finally, we obtain
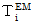 as follows :
as follows :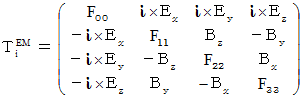
This type of the tensor is called
 antisymmetric tensor.
antisymmetric tensor.
Seting
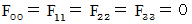 , we finish the tensor. It is
, we finish the tensor. It is  Complex number electromagnetic field tensor
Complex number electromagnetic field tensor 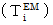 .
.
(8) Lorentz transformation comes from Maxwell's equations


Lorentz competed Lorentz transformation in 1904. Maxwell's equations keeps be satisfied regardless of Lorentz transformation. I will sum up his method of finding Lorentz transformation.
Maxwell's equations are expressed as follows without signs of operator with system of units in which the speed of light is
 as system of
as system of  units :
units :[ Equation
 ]
]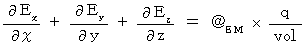
 (Equality 001)
(Equality 001)
[ Equation
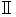 ]
]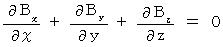
 (Equality 002)
(Equality 002)[ Equation
 ]
]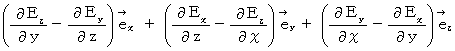
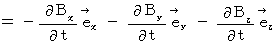
[ Equation
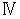 ]
]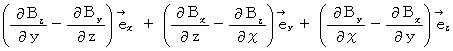
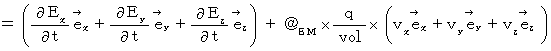
Owing to [ Equation
 ] , we obtain the following equality :
] , we obtain the following equality :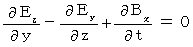
 (Equality 003)
(Equality 003)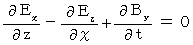
 (Equality 004)
(Equality 004)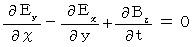
 (Equality 005)
(Equality 005)Owing to [ Equation
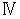 ] , we obtain the following equality :
] , we obtain the following equality :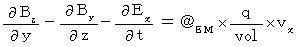
 (Equality 006)
(Equality 006)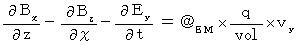
 (Equality 007)
(Equality 007)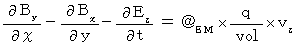
 (Equality 008)
(Equality 008)We consider that above-mentioned equalities are in the 2nd observer's coordinate system
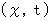 . Now, we think about the 1st observer's coordinate system
. Now, we think about the 1st observer's coordinate system 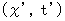 ; the 1st observer is traveling in the positive direction of the X-axis at a speed of
; the 1st observer is traveling in the positive direction of the X-axis at a speed of 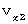 . Maxwell's equations are also satisfied in the 1st observer's coordinate systemdue to the principle of relativity. So, we express Maxwell's equations in the 1st observer's coordinate system as follows :
. Maxwell's equations are also satisfied in the 1st observer's coordinate systemdue to the principle of relativity. So, we express Maxwell's equations in the 1st observer's coordinate system as follows :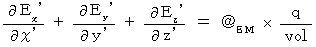
 (Equality 101)
(Equality 101)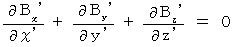
 (Equality 102)
(Equality 102)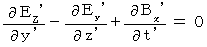
 (Equality 103)
(Equality 103)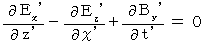
 (Equality 104)
(Equality 104)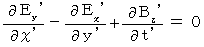
 (Equality 105)
(Equality 105)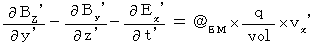
 (Equality 106)
(Equality 106)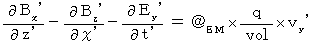
 (Equality 107)
(Equality 107)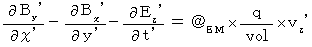
 (Equality 108)
(Equality 108)Now, let us find a coordinate conversion from the 2nd observer's coordinate system
 to the 1st observer's coordinate system
to the 1st observer's coordinate system  .
.We can express it as follows, because a coordinate conversion is a linear transformation, and because the space-time point, which satisfies
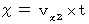 in the stationary coordinate system, is converted to the space point on which the space origin of the traveling coordinate system exists :
in the stationary coordinate system, is converted to the space point on which the space origin of the traveling coordinate system exists :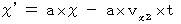
 (Equality 400)
(Equality 400)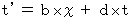
 (Equality 401)
(Equality 401) Therefore, we obtain the following equalities :
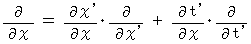
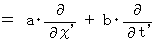
 (Equality 009)
(Equality 009)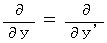
 (Equality 010)
(Equality 010)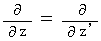
 (Equality 011)
(Equality 011)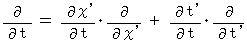
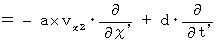
 (Equality 012)
(Equality 012)Plugging (Equality 009), (Equality 010), and (Equality 011) into (Equality 001), we obtain the following equality :
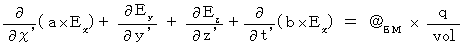
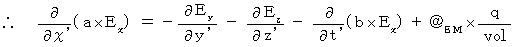
 (Equality 201)
(Equality 201)Plugging (Equality 009), (Equality 010), and (Equality 011) into (Equality 002), we obtain the following equality :
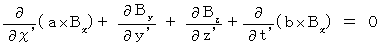
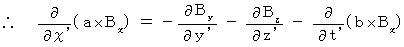
 (Equality 202)
(Equality 202)Plugging (Equality 010), (Equality 011), and (Equality 012) into (Equality 003), we obtain the following equality :
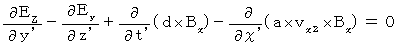
 (Equality 203)
(Equality 203)Plugging (Equality 009), (Equality 011), and (Equality 012) into (Equality 004), we obtain the following equality :
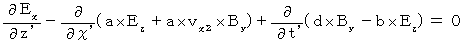
 (Equality 204)
(Equality 204)Plugging (Equality 009), (Equality 010), and (Equality 012) into (Equality 005), we obtain the following equality :
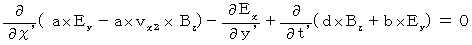
 (Equality 205)
(Equality 205)Plugging (Equality 010), (Equality 011), and (Equality 012) into (Equality 006), we obtain the following equality :
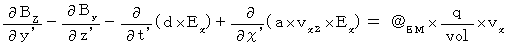
 (Equality 206)
(Equality 206)Plugging (Equality 009), (Equality 011), and (Equality 012) into (Equality 007), we obtain the following equality :
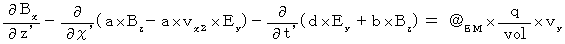
 (Equality 207)
(Equality 207)Plugging (Equality 009), (Equality 010), and (Equality 012) into (Equality 008), we obtain the following equality :
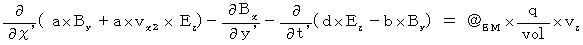
 (Equality 208)
(Equality 208) We obtain the following equalities (Equality 314)
 (Equality 338) , by comparing between the following equalities :
(Equality 338) , by comparing between the following equalities : 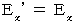
 (Equality 314)
(Equality 314)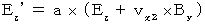
 (Equality 324)
(Equality 324)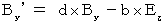
 (Equality 334)
(Equality 334)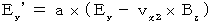
 (Equality 315)
(Equality 315)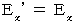
 (Equality 325)
(Equality 325)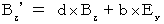
 (Equality 335)
(Equality 335)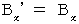
 (Equality 317)
(Equality 317)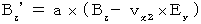
 (Equality 327)
(Equality 327)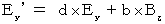
 (Equality 337)
(Equality 337)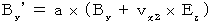
 (Equality 318)
(Equality 318)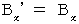
 (Equality 328)
(Equality 328)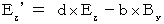
 (Equality 338)
(Equality 338)Owing to (Equality 315) and (Equality 337), we obtain the following equality :
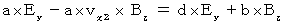
Owing to (Equality 324) and (Equality 338), we obtain the following equality :
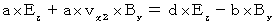
Owing to (Equality 334) and (Equality 318), we obtain the following equality :
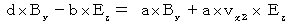
Owing to (Equality 335) and (Equality 327), we obtain the following equality :
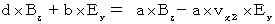
Owing to above-mentioned four equalities, we obtain the following equalities :
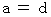
 (Equality 402)
(Equality 402)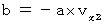
 (Equality 403)
(Equality 403)Plugging (Equality 202) into (Equality 203) , we obtain the following equality :
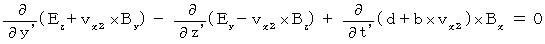
Plugging (Equality 324), (Equality 315) and (Equality 317) into this equality, we obtain the following equality :
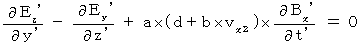
Comparing this equality with (Equality 103), we obtain the following equality :
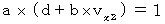
Plugging (Equality 402) and (Equality 403) into this equality, we obtain the following equality :
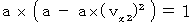
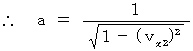
 (式404)
(式404)Plugging (Equality 404) into (Equality 402),
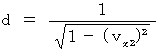
Plugging (Equality 402) into (Equality 403),
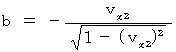
Therefore, (Equality 400) and (Equality 401) become as follows :
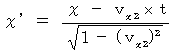
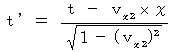
These equalities shows a coordinate conversion led by the principle that Maxwell's equations are satisfied in all inertial frames of reference.
It is
 Lorentz transformation.
Lorentz transformation.
Moreover, we find the following way of transformation on electric field and magnetic field in the process of finding Lorentz transformation :