(1) Coordinate conversion of the force between two 'amounts of electric charge'
Displacement current, magnetic field, and electric field are expressed with international system of units, i.e. SI-system of unites, as follows :
 Displacement current :
Displacement current :

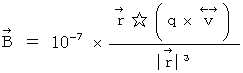
 Magnetic field :
Magnetic field :

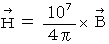
 Electric field :
Electric field :

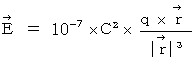
Displacement current and electric field are expressed with  system of units as follows :
system of units as follows :
 Displacement current :
Displacement current :

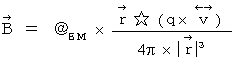
 *
* 
 Electric field :
Electric field :

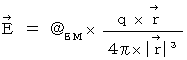
In my 'Inertial System Theory of Relativity', displacement current and electric field are replaced by 'substantial magnetic field' and 'substantial electric field', respectively. They are expressed with  system of units as follows :
system of units as follows :
 Substantial magnetic field :
Substantial magnetic field :

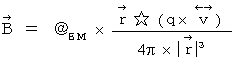
 Note : It is the same as general displacement current.
Note : It is the same as general displacement current.
 Lorentz force is expressed as follows :
Lorentz force is expressed as follows :

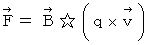
 Substantial electric field :
Substantial electric field :

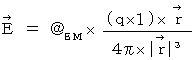
 Note :
Note : We obtain it by dividing general electric field
We obtain it by dividing general electric field
 by the speed of light.
by the speed of light.
 Coulomb's force is expressed as follows :
Coulomb's force is expressed as follows :

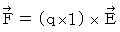
Now, let us think about coordinate conversion of the force between two 'amounts of electric charge.'
On the space origin of the 1st observer, there is the object A with amount of electric charge of 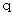 at the absolute-time point of
at the absolute-time point of 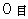 . The object A is traveling on linear uniform motion in the positive direction of X-axis at a speed of
. The object A is traveling on linear uniform motion in the positive direction of X-axis at a speed of  . The substantial electric field and substantial magnetic field, which are produced by the object A, on the space-time point
. The substantial electric field and substantial magnetic field, which are produced by the object A, on the space-time point 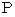 of the 1st observer's coordinate system are expressed as follows :
of the 1st observer's coordinate system are expressed as follows :

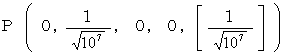
 Substantial electric field :
Substantial electric field :
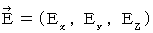
 Substantial magnetic field :
Substantial magnetic field :
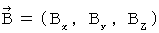
On the space-time point  of the 1st observer's coordinate system, there is the object B with amount of electric charge of
of the 1st observer's coordinate system, there is the object B with amount of electric charge of  . The object B is traveling on linear uniform motion in the positive direction of X-axis at a speed of
. The object B is traveling on linear uniform motion in the positive direction of X-axis at a speed of  .
.
Let 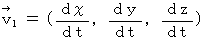 be the space velocity of the object A and the object B relative to the 1st observer.
be the space velocity of the object A and the object B relative to the 1st observer.
Then, it is 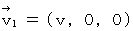 .
.
The space position vector of the space point  is as follows :
is as follows :

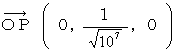
The magnitude of relative space electric current of the object A is  . The magnitude of space electric current of the object B is
. The magnitude of space electric current of the object B is 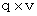 .
.
The 0th observer is traveling on linear uniform motion in the positive direction of X-axis at a speed of  relative to the 1st observer. The space-time origin of them is identical. The substantial electric field and substantial magnetic field on the space-time point
relative to the 1st observer. The space-time origin of them is identical. The substantial electric field and substantial magnetic field on the space-time point 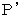 of the 0th observer's coordinate system are expressed as follows :
of the 0th observer's coordinate system are expressed as follows :

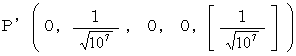
 Substantial electric field :
Substantial electric field :
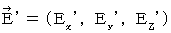
 Substantial magnetic field :
Substantial magnetic field :
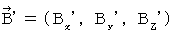
There is the stationary object A on the space origin of the 0th observer's coordinate system. There is the stationary object B on the space-time point 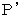 of the 0th observer's coordinate system.
of the 0th observer's coordinate system.
Let 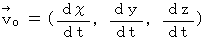 be the space velocity of the object A and the object B relative to the 0th observer.
be the space velocity of the object A and the object B relative to the 0th observer.
Then, it is 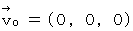 .
.
The space position vector of the space point 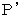 is as follows :
is as follows :

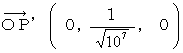
The magnitude of relative space electric current of the object A with respect to the 0th observer is  . The magnitude of space electric current of the object B with respect to the 0th observer is
. The magnitude of space electric current of the object B with respect to the 0th observer is  .
.
Firstly, let us find the electromagnetic force that the object A exerts an influence on the object B in the 1st observer's coordinate system.
First, we find the substantial electric field ( 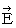 ) on the space-time point
) on the space-time point 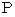 of the 1st observer's coordinate system.
of the 1st observer's coordinate system.
It is 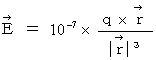 .
.
When it is  , it is
, it is 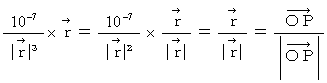 .
.
Therefore, 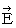 is expressed as follows :
is expressed as follows :

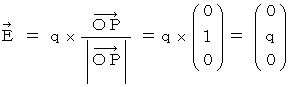
Therefore, Coulomb's force (  ) that the object A exerts an infuence on the object B is as follows :
) that the object A exerts an infuence on the object B is as follows :

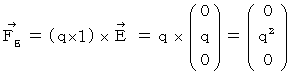
Second, we find the substantial magnetic field ( 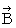 ) on the space-time point
) on the space-time point 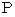 of the 1st observer's coordinate system. It is
of the 1st observer's coordinate system. It is  , because, what produces the magnetic field is not 'space electric current' but 'relative space electric current.' Therefore, Lorentz force (
, because, what produces the magnetic field is not 'space electric current' but 'relative space electric current.' Therefore, Lorentz force ( 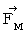 ) that the object A exerts an influence on the object B with respect to the 1st observer is
) that the object A exerts an influence on the object B with respect to the 1st observer is  .
.
Therefore, the electromagnetic force ( 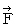 ) that the object A exerts an influence on the object B in the 1st observer's coordinate system is as follows :
) that the object A exerts an influence on the object B in the 1st observer's coordinate system is as follows :

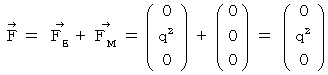
Secondly, let us find the electromagnetic force that the object A exerts an influence on the object B in the 0th observer's coordinate system.
First, we find the substantial electric field ( 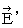 ) on the space-time
) on the space-time 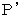 of the 0th observer's coordinate system.
of the 0th observer's coordinate system.
It is 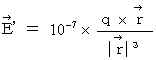 .
.
When it is 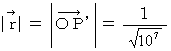 , it is
, it is 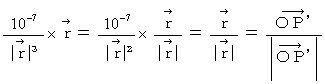 .
.
Therefore, 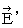 is expressed as follows :
is expressed as follows :

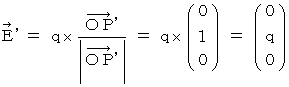
Therefore, Coulomb's force ( 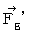 ) that the object A exerts an influence on the object B is as follows :
) that the object A exerts an influence on the object B is as follows :

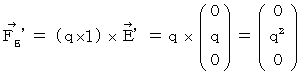
Second, we find the substantial magnetic field ( 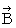 ) on the space-time point
) on the space-time point 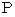 of the 0th observer's coordinate system. It is
of the 0th observer's coordinate system. It is  Therefore, Lorentz force (
Therefore, Lorentz force ( 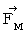 ) that the object A exerts an influence on the object B with respect to the 1st observer is
) that the object A exerts an influence on the object B with respect to the 1st observer is  .
.
Therefore, the electromagnetic force ( 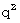 ) that the object A exerts an influence on the object B in the 0th observer's coordinate system is as follows :
) that the object A exerts an influence on the object B in the 0th observer's coordinate system is as follows :

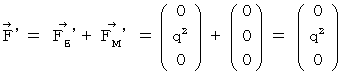
That's why the electromagnetic force that the object A exerts an influence on the object B is constant regardless of a coordinate conversion. We know 'principle of relativity' holds good to electromagnetic field.
Next, let us think about the situation like above-mentioned situation; the following situation is added :
There is the object C with amount of electric charge of 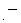
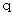 on the space origin of the 1st observers.
on the space origin of the 1st observers.
In this situation, the magnitude of relative space electric current of the object A relative to the 1st observer is 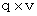 . The magnitude of space electric current of the object B relative to the 1st observer is
. The magnitude of space electric current of the object B relative to the 1st observer is 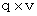 . The magnitude of relative space electric current of the object A relative to the 0th observer is
. The magnitude of relative space electric current of the object A relative to the 0th observer is 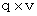 . The magnitude of space electric current of the object B relative to the 0th observer is
. The magnitude of space electric current of the object B relative to the 0th observer is  .
.
Firstly, let us find the electromagnetic force that the object A and the object C exert an influence on the object B in the 1st observer's coordinate system.
First, the substantial electric field ( 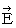 ) on the space-time point
) on the space-time point 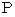 of the 1st observer's coordinate system is
of the 1st observer's coordinate system is  . Therefore, Therefore, Coulomb's force (
. Therefore, Therefore, Coulomb's force ( 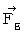 ) that the object A and the object C exert an infuence on the object B is
) that the object A and the object C exert an infuence on the object B is  .
.
Second, we find the substantial magnetic field ( 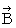 ) on the space-time point
) on the space-time point 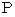 of the 1st observer's coordinate system.
of the 1st observer's coordinate system.
It is 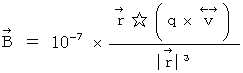 .
.
When it is  , it is
, it is 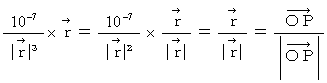 .
.
Therefore, 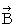 is expressed as follows :
is expressed as follows :

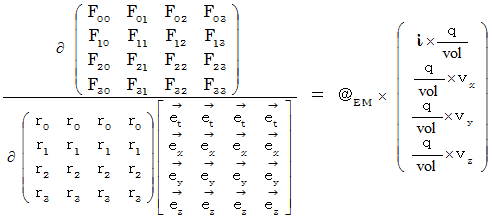
By the way, the operation 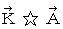 , which is the meaning to vector product
, which is the meaning to vector product  by
by 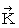 , is expressed generally as
, is expressed generally as 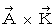 .
. 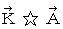 is expressed with matrix multiplication, which columns and elements consist of elements of the vectors of
is expressed with matrix multiplication, which columns and elements consist of elements of the vectors of 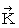 and
and 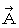 , as follows :
, as follows :

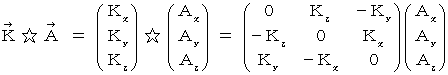


Owing to this equation, we find the substantial magnetic field as follows :

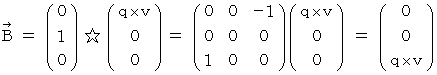
Therefore, Lorentz force ( 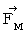 ) that the object A and the object C exert an influence on the object B is as follows :
) that the object A and the object C exert an influence on the object B is as follows :

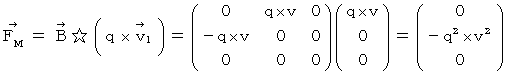
Therefore, the electromagnetic force ( 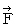 ) that the object A exerts an influence on the object B in the 1st observer's coordinate system is as follows :
) that the object A exerts an influence on the object B in the 1st observer's coordinate system is as follows :

Secondly, let us find the electromagnetic force that the object A and the object C exert an influence on the object B in the 0th observer's coordinate system.
First, the substantial electric field (  ) on the space-time
) on the space-time 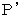 of the 0th observer's coordinate system is
of the 0th observer's coordinate system is  . Therefore, Coulomb's force (
. Therefore, Coulomb's force ( 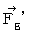 ) that the object A and the object C exert an influence on the object B is
) that the object A and the object C exert an influence on the object B is  .
.
Second, we find the substantial magnetic field ( 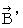 ) on the space-time point
) on the space-time point 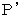 of the 0th observer's coordinate system.
of the 0th observer's coordinate system.

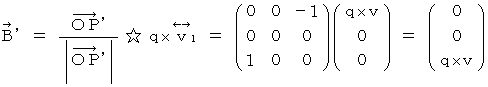
Therefore, Lorentz force ( 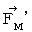 ) that the object A and the object C exert an influence on the object B is as follows :
) that the object A and the object C exert an influence on the object B is as follows :

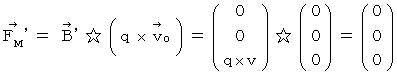
Now, we must not forget 'virtual electric field.' The substantial magnetic field ( 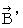 ) on the space-time point
) on the space-time point 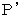 is traveling in the negative direction of the X-axis at a speed of
is traveling in the negative direction of the X-axis at a speed of  , because the speed of the substantial magnetic field is equal to the speed of the negative electric charge, which forms 'relative space electric current' which produces the substantial magnetic field. Therefore, we find that the following virtual electric field (
, because the speed of the substantial magnetic field is equal to the speed of the negative electric charge, which forms 'relative space electric current' which produces the substantial magnetic field. Therefore, we find that the following virtual electric field ( 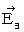 ) is produced on the space-time point
) is produced on the space-time point 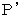 :
:

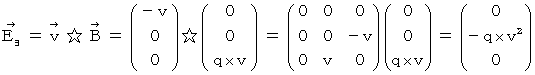
Therefore, the force ( 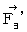 ) that the virtical electric field exerts an influence on the object B is as follows :
) that the virtical electric field exerts an influence on the object B is as follows :

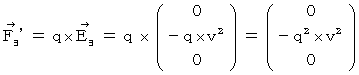
Therefore, the electromagnetic force ( 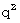 ) that the object A and the object C exert an influence on the object B in the 0th observer's coordinate system is as follows :
) that the object A and the object C exert an influence on the object B in the 0th observer's coordinate system is as follows :

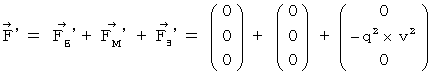
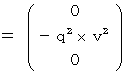
That's why the electromagnetic force that the object A and the object C exert an influence on the object B is constant regardless of a coordinate conversion. We know 'principle of relativity' holds good to electromagnetic field.
(2) The Collapsed effort to unify completely electric field and magnetic field
Under the view of Faraday who discovered that light is a kind of electromagnetic, we might be able to think as follows :
 Electro field and magnetic field are nothing but different form of identical electromagnetic field. They are the identical physical item. Their ratio of composition of electromagnetic wave changes owing to a point of view.
Electro field and magnetic field are nothing but different form of identical electromagnetic field. They are the identical physical item. Their ratio of composition of electromagnetic wave changes owing to a point of view.
So, let us change 'law of vibration of photon on electromagnetic field' for the moment as follows :
 Frequency of vibrations, that is number of vibration per unit absolute time interval, of a photon on electromagnetic field in an object, i.e. amount of electric charge, is constant with respect to every observers traveling with linear uniform motion with various velocity. Vibration of photon on electromagnetic field in an object is decomposed into space axes components and relative-time axis component. And then, each component of vibration travels through space at a speed of
Frequency of vibrations, that is number of vibration per unit absolute time interval, of a photon on electromagnetic field in an object, i.e. amount of electric charge, is constant with respect to every observers traveling with linear uniform motion with various velocity. Vibration of photon on electromagnetic field in an object is decomposed into space axes components and relative-time axis component. And then, each component of vibration travels through space at a speed of  . The former forms magnetic field and then produces Lorentz force. The latter forms electric field and then produces Coulomb's force.
. The former forms magnetic field and then produces Lorentz force. The latter forms electric field and then produces Coulomb's force.
Then, Coulomb's force is expressed as follows :

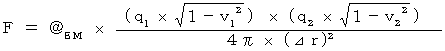
We consider what produces electric field is not 'four-dimensional space-time electric current' but 'relative-time electric current.' This change looks natural.
Then, 'substantial electric field' and Coulomb's force are expressed as follows, respectively :

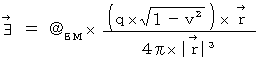

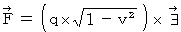
Moreover, We consider what produces magnetic field is not 'relative space electric current' but 'space electric current' as follows :

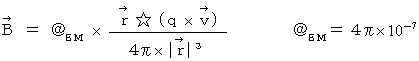
It looks natural.
Now, let us think about a coordinate conversion of the force between two amounts of electric charges traveling with the same velocity. Let the situation be the same as the above-mentioned firstly; there is not the object C.
Then, the magnitude of relative-time electric current of the object A relative to the 1st observer is 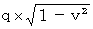 . The magnitude of space electric current of the object B relative to the 1st observer is
. The magnitude of space electric current of the object B relative to the 1st observer is 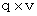 . The magnitude of relative-time electric current of the object A relative to the 0th observer is
. The magnitude of relative-time electric current of the object A relative to the 0th observer is 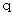 . The magnitude of space electric current of the object B relative to the 0th observer is
. The magnitude of space electric current of the object B relative to the 0th observer is  .
.
Firstly, let us find the electromagnetic force that the object A exerts an influence on the object B in the 1st observer's coordinate system.
First, we find the substantial electric field( 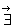 )on the space-time point
)on the space-time point 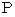 of the 1st observer's coordinate system.
of the 1st observer's coordinate system.
It is 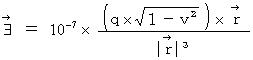 .
.
When it is 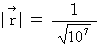 , it is
, it is 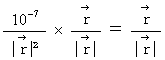 .
.
Therefore, 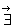 is expressed as follows :
is expressed as follows :

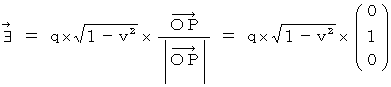

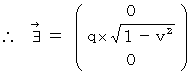
Second, we find the substantial magnetic field( 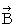 )on the space-time point
)on the space-time point 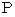 of the 1st observer's coordinate system.
of the 1st observer's coordinate system.

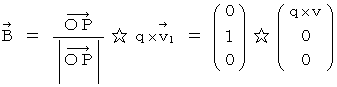

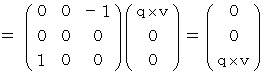
Well, we obtain  Four-dimensional electromagnetic force
Four-dimensional electromagnetic force 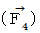
 by making
by making  Electromagnetic field tensor
Electromagnetic field tensor 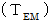
 exert an influence on
exert an influence on  Four-dimensional space-time electric current.
Four-dimensional space-time electric current. 

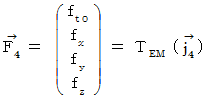

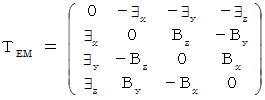

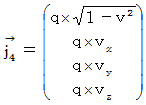
 That is,
That is,

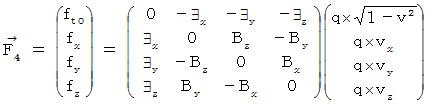

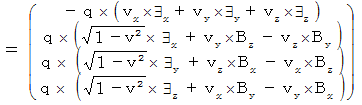
 Proviso :
Proviso :
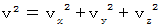
* Notes :


 Lorenz force is expressed as follows :
Lorenz force is expressed as follows :

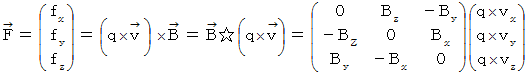

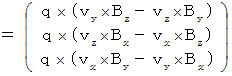


 Coulomb's force is expressed as follows :
Coulomb's force is expressed as follows :

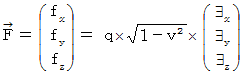



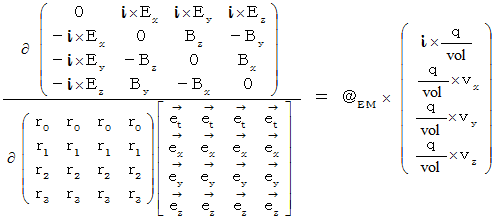
 is called
is called  Electromagnetic field antisymmetric covariant tensor
Electromagnetic field antisymmetric covariant tensor , too. There is the following
, too. There is the following  Electromagnetic field antisymmetric contravariant tensor
Electromagnetic field antisymmetric contravariant tensor 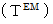
 :
:

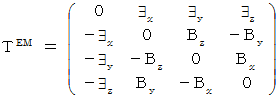
I figured out the following  Complex number electromagnetic field tensor
Complex number electromagnetic field tensor 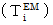 .
. :
:

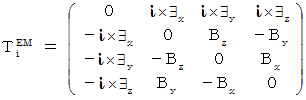
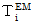 is the tensor which elements of
is the tensor which elements of  Electromagnetic field antisymmetric contravariant tensor
Electromagnetic field antisymmetric contravariant tensor in the first column or the first row are replaced with imaginary number.
in the first column or the first row are replaced with imaginary number.  Four-dimensional electromagnetic force
Four-dimensional electromagnetic force 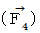
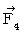
 is expressed as follows with
is expressed as follows with  complex number electromagnetic field tensor.
complex number electromagnetic field tensor. 

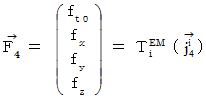

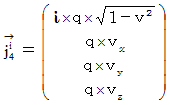
 I call
I call 
 complex number four-dimensional
complex number four-dimensional
 space-time electric current.
space-time electric current.
 That is,
That is,

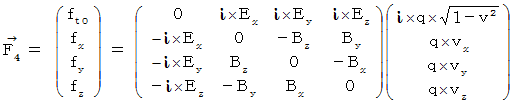

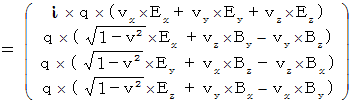
Let us go back to the point where we started. Let us find the electromagnetic force that the object A exerts an influence on the object B with respect to the 1st observer. In the coordinate system of the 1st observer, the electromagnetic force ( 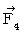 ) that the object A exerts an influence on the object B is obtained as follows by making
) that the object A exerts an influence on the object B is obtained as follows by making  Electromagnetic field antisymmetric covariant tensor
Electromagnetic field antisymmetric covariant tensor 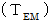
 exert an influence on
exert an influence on  Four-dimensional space-time electric current.
Four-dimensional space-time electric current.  :
:

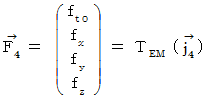

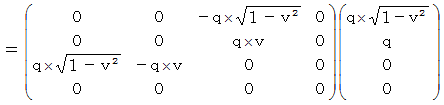

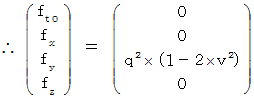
Secondly, let us find the electromagnetic force that the object A exerts an influence on the object B in the 0th observer's coordinate system.
First, we find the substantial electric field (  ) on the space-time
) on the space-time  of the 0th observer's coordinate system. We obtain it with the same way as above-mentioned.
of the 0th observer's coordinate system. We obtain it with the same way as above-mentioned.

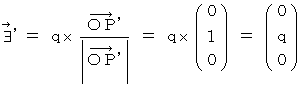
Second, we find the substantial magnetic field ( 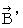 ) on the space-time point
) on the space-time point 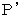 of the 0th observer's coordinate system. It is
of the 0th observer's coordinate system. It is  .
.
Therefore, the  four-dimensional electromagnetic force
four-dimensional electromagnetic force 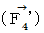
 that the object A exerts an influence on the object B with respect to the 0th observer is as follows :
that the object A exerts an influence on the object B with respect to the 0th observer is as follows :

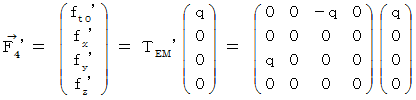

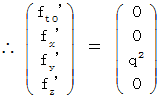
Therefore, it is 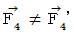 . That is, we find that the electromagnetic force that the object A exerts an influence on the object B changes due to a coordinate conversion. Actually, it was hoped that the hypotheses make the force constant regardless of a coordinate conversion and hold 'principle of relativity' good. But, it's a pity that it disappointed our expectations. If the force between two conductors with the same direction of electric current would be not attraction but counter attraction, everything goes well. Actually, it is attraction.
. That is, we find that the electromagnetic force that the object A exerts an influence on the object B changes due to a coordinate conversion. Actually, it was hoped that the hypotheses make the force constant regardless of a coordinate conversion and hold 'principle of relativity' good. But, it's a pity that it disappointed our expectations. If the force between two conductors with the same direction of electric current would be not attraction but counter attraction, everything goes well. Actually, it is attraction.
However, it is too early to give up. Now, let us find 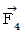 and
and 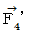 with
with  Electromagnetic field antisymmetric contravariant tensor.
Electromagnetic field antisymmetric contravariant tensor. 

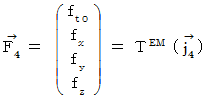

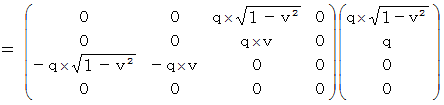

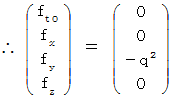

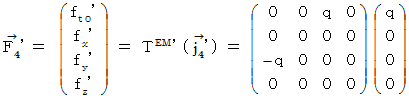

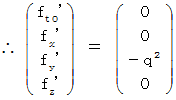
Therefore, it is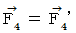 . But, it looks strange. Why it is
. But, it looks strange. Why it is 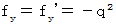 instead of
instead of 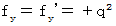 ? If it is
? If it is 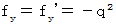 , the force between electric charges with the same number becomes attraction; it is repulsive force actually. Therefore, this method did not make it, too.
, the force between electric charges with the same number becomes attraction; it is repulsive force actually. Therefore, this method did not make it, too.
So, this is where  Complex number electromagnetic field tensor
Complex number electromagnetic field tensor 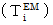
 comes in. Let us find
comes in. Let us find 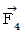 and
and 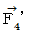 with
with 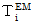 .
.

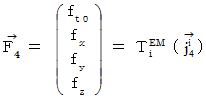

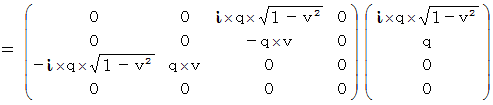

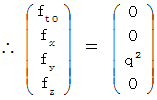

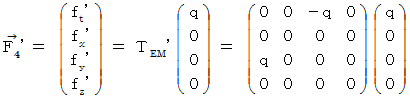

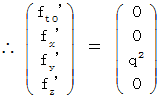
Therefore, it is 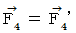 and
and 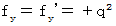 . Then, we feel a whole lot better. I, however, don't feel better. I think that something only
. Then, we feel a whole lot better. I, however, don't feel better. I think that something only  Complex number electromagnetic field tensor
Complex number electromagnetic field tensor 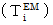
 can explain is wrong. I don't accept Minkowski's space-time, which accepts imaginary time, as space-time in physics. Therefore, the hypotheses in this corner are all turned down.
can explain is wrong. I don't accept Minkowski's space-time, which accepts imaginary time, as space-time in physics. Therefore, the hypotheses in this corner are all turned down.
(3) Maxwell's equations have mystery of complex number electromagnetic field
There is electromagnetic field in Minkowski's four-dimensional space-time. An object with electric charge is exerted an influence on by  four-dimensional force
four-dimensional force , because the object produces
, because the object produces  four-dimensional electric current.
four-dimensional electric current.
 Complex number electromagnetic field tensor
Complex number electromagnetic field tensor 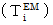
 shows a state of electromagnetic field on one space-time point. It is a antisymmetric matrix with four columns and four rows, and it consists of six kinds of element and the element of 0.
shows a state of electromagnetic field on one space-time point. It is a antisymmetric matrix with four columns and four rows, and it consists of six kinds of element and the element of 0.

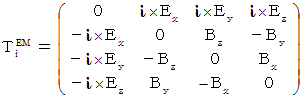
 Note :
Note :
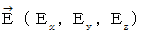 is a substantial electric field.
is a substantial electric field.
 A substantial electric field is electric field is
A substantial electric field is electric field is
 obtained by dividing an electric field by a speed
obtained by dividing an electric field by a speed
 of light. A substantial electric field is the same
of light. A substantial electric field is the same
 as an electric field in the system of
as an electric field in the system of 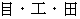
 units.
units.
We obtain  Complex number four-dimensional electromagnetic force
Complex number four-dimensional electromagnetic force  by making
by making  Complex number electromagnetic field tensor
Complex number electromagnetic field tensor  exert an influence on
exert an influence on  Complex number four-dimensional space-time electric current.
Complex number four-dimensional space-time electric current.

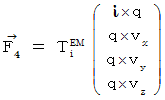
Maxwell's equations shows the relationship of elements of  Complex number electromagnetic field tensor
Complex number electromagnetic field tensor , and it has the following stealthy law :
, and it has the following stealthy law :
 We obtain
We obtain  Complex number four-dimensional space-time electric current density
Complex number four-dimensional space-time electric current density multiplied by
multiplied by  Electromagnetic transmittance
Electromagnetic transmittance by partial differentiating
by partial differentiating  Complex number electromagnetic field tensor
Complex number electromagnetic field tensor in Minkowski's four-dimensional space-time.
in Minkowski's four-dimensional space-time.
I will explain above-mentioned state.
We express  Complex number electromagnetic field tensor
Complex number electromagnetic field tensor 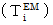
 as follows with elements of
as follows with elements of 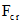 :
:

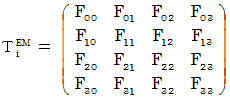
We express four-dimensional space-time coordinate 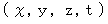 as follows with
as follows with 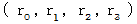 :
:

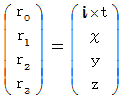
Let us find how to express Maxwell's equation with elements 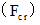 of complex number electromagnetic field tensor and four-dimensional space-time coordinates
of complex number electromagnetic field tensor and four-dimensional space-time coordinates 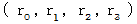 .
.
Maxwell's equation ( system of  units ) :
units ) :
 [ Equation
[ Equation  ]
]
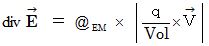
 [ Equation
[ Equation  ]
]
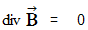
 [ Equation
[ Equation  ]
]
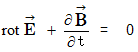
 [ Equation
[ Equation 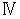 ]
]
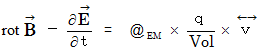
First, Maxwell's equations are shown as follows without signs of operators :
[ Equation 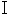 ]
]

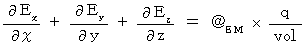

 (Equality 001)
(Equality 001)

 Proviso :
Proviso :

[ Equation 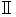 ]
]

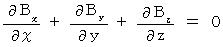

 (Equality 002)
(Equality 002)
[ Equation  ]
]

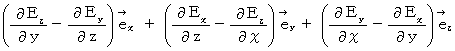

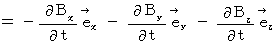
[ Equation 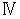 ]
]

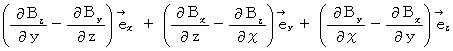

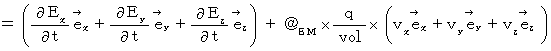
Owing to [ Equation  ] , we obtain the following equalities :
] , we obtain the following equalities :

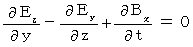

 (Equality 003)
(Equality 003)

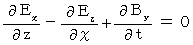

 (Equality 004)
(Equality 004)

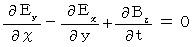

 (Equality 005)
(Equality 005)
Owing to [ Equation 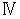 ] , we obtain the following equalities :
] , we obtain the following equalities :

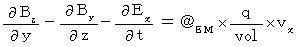

 (Equality 006)
(Equality 006)

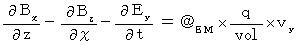

 (Equality 007)
(Equality 007)

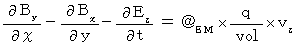

 (Equality 008)
(Equality 008)
First, we integrate [ Equation  ] and [ Equation
] and [ Equation  ] .
] .
Owing to (Equality 002), we obtain the following equality :

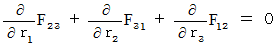

 (Equality 002' )
(Equality 002' )
Owing to (Equality 003), we obtain the following equality :

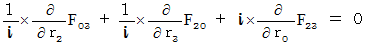

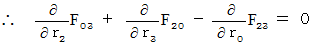

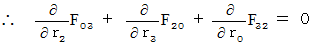

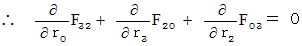

 (Equality 003' )
(Equality 003' )
Owing to (Equality 004), we obtain the following equality :

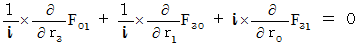

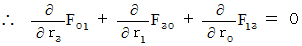

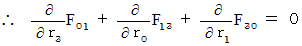

 (Equality 004' )
(Equality 004' )
Owing to (Equality 005), we obtain the following equality :

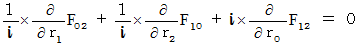

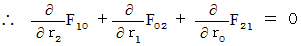

 (Equality 005' )
(Equality 005' )
We can integrate four equalities of (Equality 002' ) 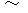 (Equality 005' ) into the following equality :
(Equality 005' ) into the following equality :

 Note :
Note :
 are different integers of
are different integers of 
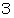 , respectively.
, respectively.

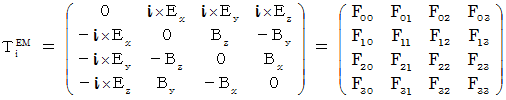
Next, we integrate [ Equation  ] and [ Equation
] and [ Equation 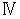 ] .
] .
Owing to (Equality 001), we obtain the following equality :

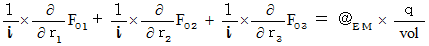

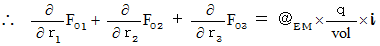

 (Equality 001' )
(Equality 001' )
Owing to (Equality 006), we obtain the following equality :

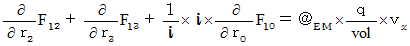

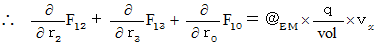

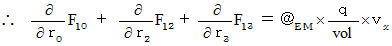

 (Equality 006' )
(Equality 006' )
Owing to (Equality 007), we obtain the following equality :

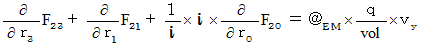

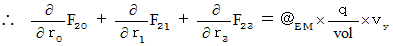

 (Equality 007' )
(Equality 007' )
Owing to (Equality 008), we obtain the following equality :

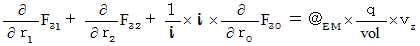

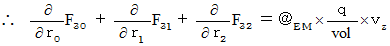

 (Equality 008' )
(Equality 008' )
I show side by side four equalities of (Equality 001' ) and (Equality 006' ) 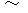 (Equality 008' ) .
(Equality 008' ) .

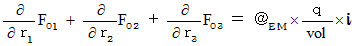

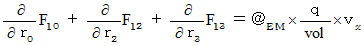

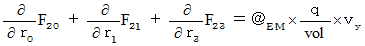

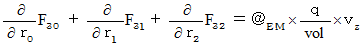
Owing to 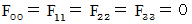 , these four equalities are expressed as follows :
, these four equalities are expressed as follows :

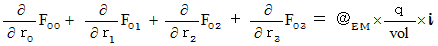

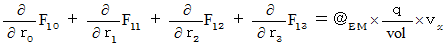

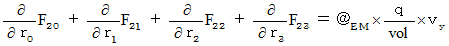

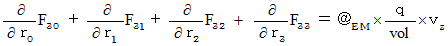
We can integrate these four equalities into the following one :

Therefore, we obtain the following equality :

 Note :
Note : We express a vector :
We express a vector : 
 as follows :
as follows :

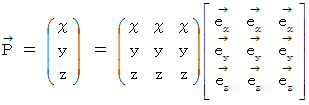
 We obtain a vector by partial differentiating a
We obtain a vector by partial differentiating a
 tensor by a vector.
tensor by a vector.
This equality is expressed as follows :

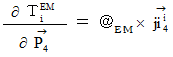

 :
: Four-dimensional space-time position vector
Four-dimensional space-time position vector

 :
: Conplex number four-dimensional space-time electric
Conplex number four-dimensional space-time electric
 current density
current density

 :
: Conplex number electromagnetic field tensor
Conplex number electromagnetic field tensor

 :
: Electromagnetic transmittance
Electromagnetic transmittance

(4) Discovery of electromagnetic wave
Two-principle of the special theory of relativity is 'principle of relativity' and 'constancy of the speed of light.' The root of the special theory of relativity is 'Lorentz transformation.' Adaptation of 'principle of relativity' to 'Maxwell's equations' brings 'Lorentz transformation.' 'Constancy of the speed of light' brings 'Lorentz transformation', too. Lorentz realized the former, and Einstein realized the latter. Lorentz realized it earlier than Einstein a little.
I think that we should call light electromagnetic wave in physics. Because light is electromagnetic wave, which can be observed by human, and physics must be told from a viewpoint of not human but nature. If we do it, it is easy to understand that electric field and magnetic field, with which Maxwell's equations deal, have close relations with light. Electric field and magnetic field, which are produced by a traveling electric charge, travel through space. For example, a stationary electric charge produces electric field, and then electric field transmits through space. It is not like hearing someone shouts but like massage game in a low voice by many people. However, Electric field transmits without medium; many people correspond to medium in this case. If the electric charge begins simple harmonic motion, which is one of transportation vibrations, the electric charge produces not only electric field but also magnetic field. How do they transmit through space? Everybody should think that speeds of them are equal to the speed of electric field produced by the stationary electric charge. Simple harmonic motion of an electric charge produces simple harmonic motion of electric field on the around space point on the perpendicular line to the orbit of the electric charge. Then, the simple harmonic motion of electric field produces simple harmonic motion of magnetic field. And then, the simple harmonic motion of magnetic field produced simple harmonic motion of electric field. This endless turning circle of electric field and magnetic field formed electromagnetic wave. The phase of vibration of electromagnetic wave on one space-point transmits to the next space point with time dilation like wave of the surface of the water. Electromagnetic wave transmits and spreads as transverse wave. The speed of traveling of electromagnetic wave is equal to the speed of traveling of electric field and magnetic field.
We make electric field and magnetic field be four-dimension as follows :
 Substantial electric field :
Substantial electric field : 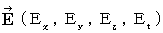
 Substantial magnetic field :
Substantial magnetic field : 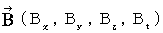
The following equations can be valid :

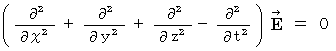


 (Equality 22-1)
(Equality 22-1)

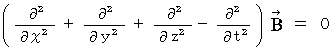


 (Equality 22-2)
(Equality 22-2)
I explain these equations.
Before my explanation, please see the following basic formulas on a vector analysis :
 Scalar :
Scalar : 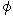
 Vector :
Vector : 

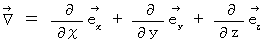
 ( Hamilton operator )
( Hamilton operator )

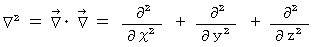
 ( Laplace operator
( Laplace operator  )
)
 Graduation :
Graduation :
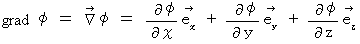

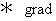 is an operator which changes scalar to vector.
is an operator which changes scalar to vector.
 Diversion :
Diversion :
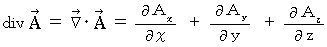

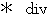 is an operator which changes vector to scalar.
is an operator which changes vector to scalar.
 Rotation :
Rotation :
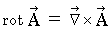

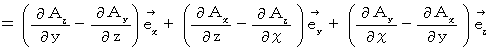

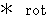 is an operator which changes vector to vector.
is an operator which changes vector to vector.

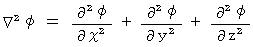

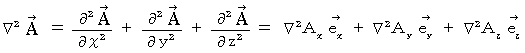
Now, let us get down to the main subject. We begin from Maxwell's equations which collect some axiom on electromagnetics.
Maxwell's equations in the space in which no amount of electric charge exists :

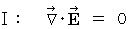



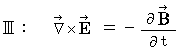

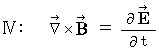
Owing to an axiom on electromagnetic and Maxwell's equation 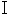 , we obtain the following equality :
, we obtain the following equality :

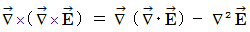

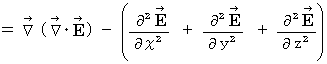

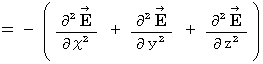


 (Equality 22-3)
(Equality 22-3)
Owing to an axiom on electromagnetic and Maxwell's equation  and
and  , we obtain the following equality :
, we obtain the following equality :

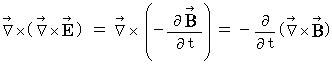

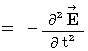


 (Equality 22-4)
(Equality 22-4)
Owing to (Equality 22-3) and (Equality 22-4), we obtain the following equality :

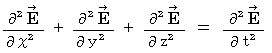

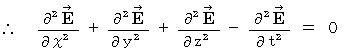
The componential label of this equality is as follows :

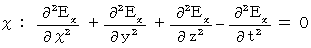

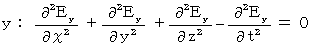

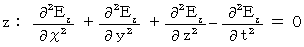

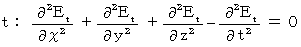
Owing to an axiom on electromagnetic and Maxwell's equation 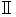
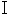 , we obtain the following equality :
, we obtain the following equality :

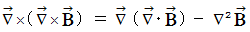

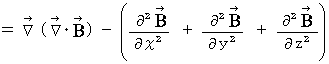

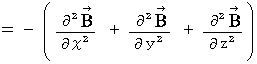


 (Equality 22-5)
(Equality 22-5)
Owing to Maxwell's equation  and
and  , we obtain the following equality :
, we obtain the following equality :

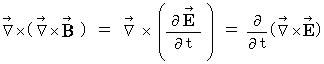

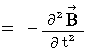


 (Equality 22-6)
(Equality 22-6)
Owing to (Equality 22-5) and (Equality 22-6), we obtain the following equality :

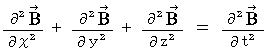

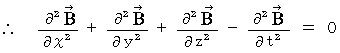
That is why (Equality 22-1) and (Equality 22-2) on electric field and magnetic field is valid in the space in which no amount of electric charge exists.
The form of (Equality 22-1) and (Equality 22-2) is called 'wave equation.'
The form of a wave equation is as follows :

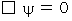
 Let
Let 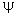 be a wave function :
be a wave function : 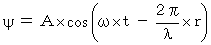

 shows D'Alembert operator :
shows D'Alembert operator :
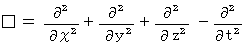
Therefore, for example, we think the wave equation of electric field as follows :

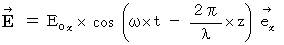
It shows a wave which vibrates only in the X-axis direction and transmits only in the Z-axis direction. This equation is the same as follows :

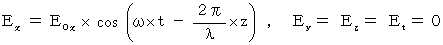
I show that this equation makes the following equations be satisfied :

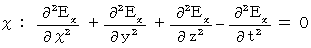

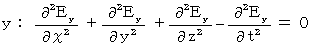

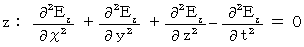

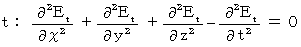
It is clear that these equations of Y, Z, and T-axis component, because it is as follows :

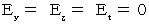
With respect to X-axis component, we only have to show as follows :

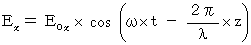 makes
makes 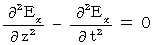 be satisfied.
be satisfied.
Let us do it.

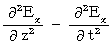

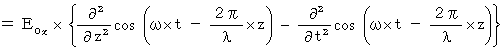

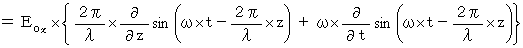

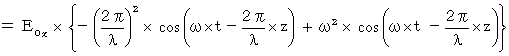

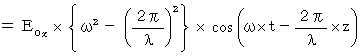
Owing to the equation :
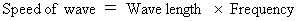 , we obtain the following equality :
, we obtain the following equality :

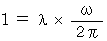

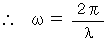
Therefore, we obtain the following equation :

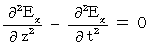
We plug the following equation into the Maxwell's equation  :
:

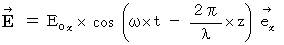
Then, we obtain the left-hand side of the Maxwell's equation  as follows :
as follows :

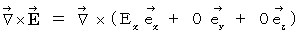



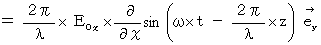
Therefore, the Maxwell's equation  becomes as follows :
becomes as follows :

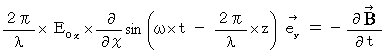
Therefore, we obtain the following equation :

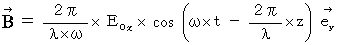
Owing to the equation :
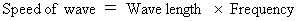 , we obtain the following equality :
, we obtain the following equality :

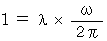
Therefore, we obtain the following equality :

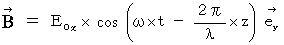
After all, we obtain the following equations :

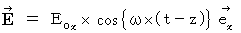

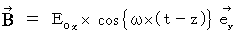
Owing to these equations, we notice in electromagnetic wave. The electromagnetic wave consists of the same phase and the same amplitude of electric field and magnetic field, which vibrate in the perpendicular direction each other, and transmits at a speed of  in the direction of the vector
in the direction of the vector  .
.
 PREVIOUS
PREVIOUS CONTENTS
CONTENTS NEXT
NEXT
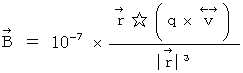
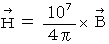
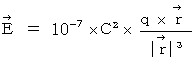
 system of units as follows :
system of units as follows :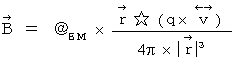

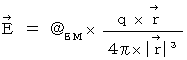
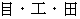 system of units as follows :
system of units as follows :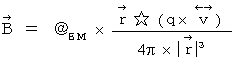
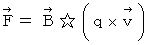
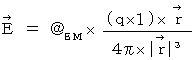
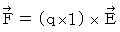
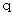 at the absolute-time point of
at the absolute-time point of 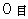 . The object A is traveling on linear uniform motion in the positive direction of X-axis at a speed of
. The object A is traveling on linear uniform motion in the positive direction of X-axis at a speed of  . The substantial electric field and substantial magnetic field, which are produced by the object A, on the space-time point
. The substantial electric field and substantial magnetic field, which are produced by the object A, on the space-time point 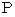 of the 1st observer's coordinate system are expressed as follows :
of the 1st observer's coordinate system are expressed as follows :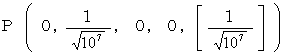
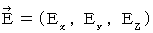
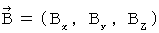
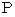 of the 1st observer's coordinate system, there is the object B with amount of electric charge of
of the 1st observer's coordinate system, there is the object B with amount of electric charge of 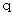 . The object B is traveling on linear uniform motion in the positive direction of X-axis at a speed of
. The object B is traveling on linear uniform motion in the positive direction of X-axis at a speed of  .
.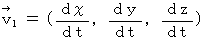 be the space velocity of the object A and the object B relative to the 1st observer.
be the space velocity of the object A and the object B relative to the 1st observer.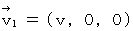 .
. is as follows :
is as follows :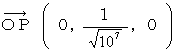
 . The magnitude of space electric current of the object B is
. The magnitude of space electric current of the object B is 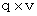 .
. relative to the 1st observer. The space-time origin of them is identical. The substantial electric field and substantial magnetic field on the space-time point
relative to the 1st observer. The space-time origin of them is identical. The substantial electric field and substantial magnetic field on the space-time point 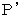 of the 0th observer's coordinate system are expressed as follows :
of the 0th observer's coordinate system are expressed as follows :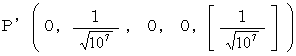
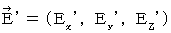
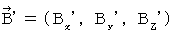
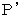 of the 0th observer's coordinate system.
of the 0th observer's coordinate system.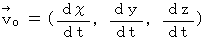 be the space velocity of the object A and the object B relative to the 0th observer.
be the space velocity of the object A and the object B relative to the 0th observer.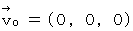 .
.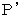 is as follows :
is as follows :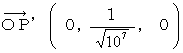
 . The magnitude of space electric current of the object B with respect to the 0th observer is
. The magnitude of space electric current of the object B with respect to the 0th observer is  .
.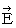 ) on the space-time point
) on the space-time point 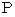 of the 1st observer's coordinate system.
of the 1st observer's coordinate system.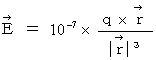 .
. , it is
, it is 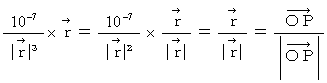 .
.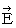 is expressed as follows :
is expressed as follows :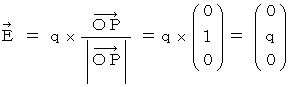
 ) that the object A exerts an infuence on the object B is as follows :
) that the object A exerts an infuence on the object B is as follows :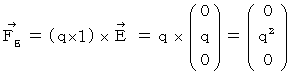
 ) on the space-time point
) on the space-time point 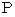 of the 1st observer's coordinate system. It is
of the 1st observer's coordinate system. It is  , because, what produces the magnetic field is not 'space electric current' but 'relative space electric current.' Therefore, Lorentz force (
, because, what produces the magnetic field is not 'space electric current' but 'relative space electric current.' Therefore, Lorentz force ( 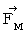 ) that the object A exerts an influence on the object B with respect to the 1st observer is
) that the object A exerts an influence on the object B with respect to the 1st observer is  .
.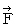 ) that the object A exerts an influence on the object B in the 1st observer's coordinate system is as follows :
) that the object A exerts an influence on the object B in the 1st observer's coordinate system is as follows :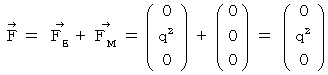
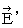 ) on the space-time
) on the space-time 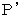 of the 0th observer's coordinate system.
of the 0th observer's coordinate system.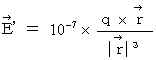 .
.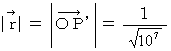 , it is
, it is 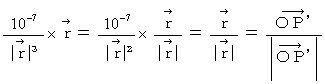 .
.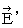 is expressed as follows :
is expressed as follows :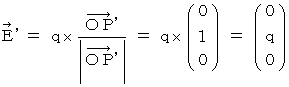
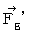 ) that the object A exerts an influence on the object B is as follows :
) that the object A exerts an influence on the object B is as follows :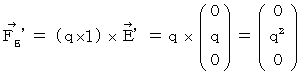
 ) on the space-time point
) on the space-time point  of the 0th observer's coordinate system. It is
of the 0th observer's coordinate system. It is  Therefore, Lorentz force (
Therefore, Lorentz force (  ) that the object A exerts an influence on the object B with respect to the 1st observer is
) that the object A exerts an influence on the object B with respect to the 1st observer is  .
.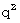 ) that the object A exerts an influence on the object B in the 0th observer's coordinate system is as follows :
) that the object A exerts an influence on the object B in the 0th observer's coordinate system is as follows :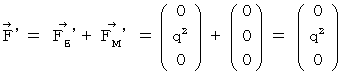
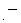
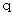 on the space origin of the 1st observers.
on the space origin of the 1st observers.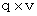 . The magnitude of space electric current of the object B relative to the 1st observer is
. The magnitude of space electric current of the object B relative to the 1st observer is 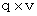 . The magnitude of relative space electric current of the object A relative to the 0th observer is
. The magnitude of relative space electric current of the object A relative to the 0th observer is 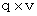 . The magnitude of space electric current of the object B relative to the 0th observer is
. The magnitude of space electric current of the object B relative to the 0th observer is  .
.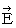 ) on the space-time point
) on the space-time point 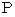 of the 1st observer's coordinate system is
of the 1st observer's coordinate system is  . Therefore, Therefore, Coulomb's force (
. Therefore, Therefore, Coulomb's force ( 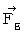 ) that the object A and the object C exert an infuence on the object B is
) that the object A and the object C exert an infuence on the object B is  .
.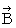 ) on the space-time point
) on the space-time point 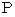 of the 1st observer's coordinate system.
of the 1st observer's coordinate system.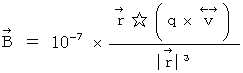 .
. , it is
, it is 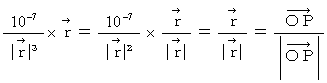 .
.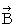 is expressed as follows :
is expressed as follows :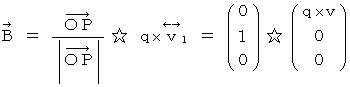
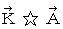 , which is the meaning to vector product
, which is the meaning to vector product 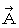 by
by 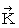 , is expressed generally as
, is expressed generally as 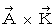 .
. 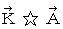 is expressed with matrix multiplication, which columns and elements consist of elements of the vectors of
is expressed with matrix multiplication, which columns and elements consist of elements of the vectors of 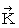 and
and 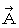 , as follows :
, as follows :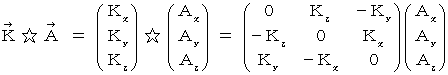

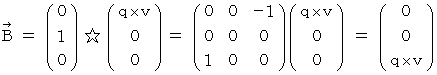
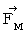 ) that the object A and the object C exert an influence on the object B is as follows :
) that the object A and the object C exert an influence on the object B is as follows :
 ) that the object A exerts an influence on the object B in the 1st observer's coordinate system is as follows :
) that the object A exerts an influence on the object B in the 1st observer's coordinate system is as follows :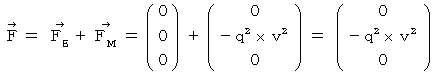
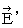 ) on the space-time
) on the space-time 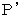 of the 0th observer's coordinate system is
of the 0th observer's coordinate system is  . Therefore, Coulomb's force (
. Therefore, Coulomb's force ( 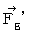 ) that the object A and the object C exert an influence on the object B is
) that the object A and the object C exert an influence on the object B is  .
.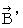 ) on the space-time point
) on the space-time point  of the 0th observer's coordinate system.
of the 0th observer's coordinate system.
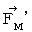 ) that the object A and the object C exert an influence on the object B is as follows :
) that the object A and the object C exert an influence on the object B is as follows :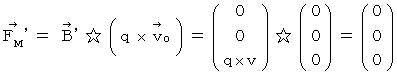
 ) on the space-time point
) on the space-time point  is traveling in the negative direction of the X-axis at a speed of
is traveling in the negative direction of the X-axis at a speed of  , because the speed of the substantial magnetic field is equal to the speed of the negative electric charge, which forms 'relative space electric current' which produces the substantial magnetic field. Therefore, we find that the following virtual electric field (
, because the speed of the substantial magnetic field is equal to the speed of the negative electric charge, which forms 'relative space electric current' which produces the substantial magnetic field. Therefore, we find that the following virtual electric field ( 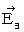 ) is produced on the space-time point
) is produced on the space-time point 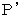 :
: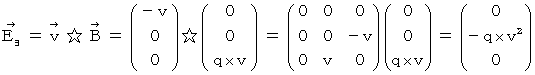
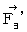 ) that the virtical electric field exerts an influence on the object B is as follows :
) that the virtical electric field exerts an influence on the object B is as follows :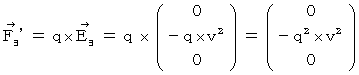
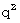 ) that the object A and the object C exert an influence on the object B in the 0th observer's coordinate system is as follows :
) that the object A and the object C exert an influence on the object B in the 0th observer's coordinate system is as follows :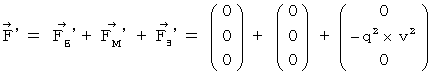
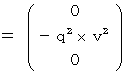
 Electro field and magnetic field are nothing but different form of identical electromagnetic field. They are the identical physical item. Their ratio of composition of electromagnetic wave changes owing to a point of view.
Electro field and magnetic field are nothing but different form of identical electromagnetic field. They are the identical physical item. Their ratio of composition of electromagnetic wave changes owing to a point of view.
 Frequency of vibrations, that is number of vibration per unit absolute time interval, of a photon on electromagnetic field in an object, i.e. amount of electric charge, is constant with respect to every observers traveling with linear uniform motion with various velocity. Vibration of photon on electromagnetic field in an object is decomposed into space axes components and relative-time axis component. And then, each component of vibration travels through space at a speed of
Frequency of vibrations, that is number of vibration per unit absolute time interval, of a photon on electromagnetic field in an object, i.e. amount of electric charge, is constant with respect to every observers traveling with linear uniform motion with various velocity. Vibration of photon on electromagnetic field in an object is decomposed into space axes components and relative-time axis component. And then, each component of vibration travels through space at a speed of  . The former forms magnetic field and then produces Lorentz force. The latter forms electric field and then produces Coulomb's force.
. The former forms magnetic field and then produces Lorentz force. The latter forms electric field and then produces Coulomb's force.
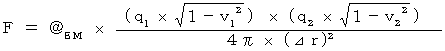
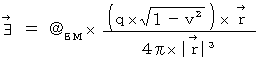
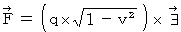
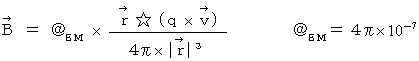
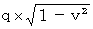 . The magnitude of space electric current of the object B relative to the 1st observer is
. The magnitude of space electric current of the object B relative to the 1st observer is 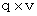 . The magnitude of relative-time electric current of the object A relative to the 0th observer is
. The magnitude of relative-time electric current of the object A relative to the 0th observer is 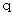 . The magnitude of space electric current of the object B relative to the 0th observer is
. The magnitude of space electric current of the object B relative to the 0th observer is  .
.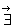 )on the space-time point
)on the space-time point 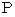 of the 1st observer's coordinate system.
of the 1st observer's coordinate system.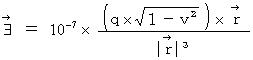 .
.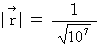 , it is
, it is 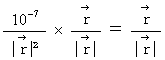 .
.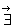 is expressed as follows :
is expressed as follows :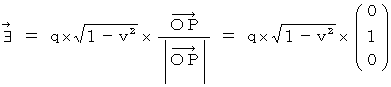
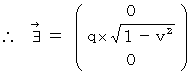
 )on the space-time point
)on the space-time point  of the 1st observer's coordinate system.
of the 1st observer's coordinate system.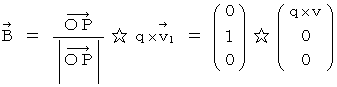
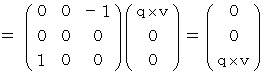
 Four-dimensional electromagnetic force
Four-dimensional electromagnetic force 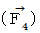
 by making
by making  Electromagnetic field tensor
Electromagnetic field tensor 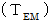
 exert an influence on
exert an influence on  Four-dimensional space-time electric current.
Four-dimensional space-time electric current. 
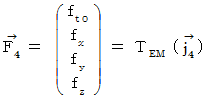
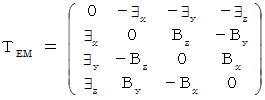
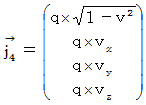
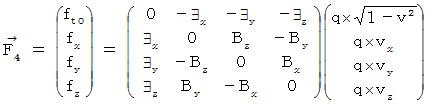
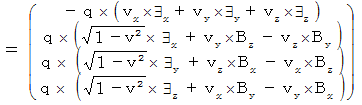

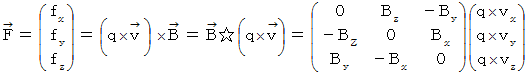
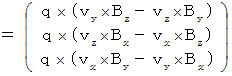

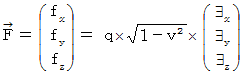

 is called
is called  Electromagnetic field antisymmetric covariant tensor
Electromagnetic field antisymmetric covariant tensor , too. There is the following
, too. There is the following  Electromagnetic field antisymmetric contravariant tensor
Electromagnetic field antisymmetric contravariant tensor 
 :
: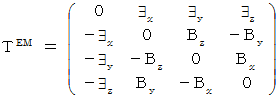
 Complex number electromagnetic field tensor
Complex number electromagnetic field tensor 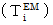 .
. :
: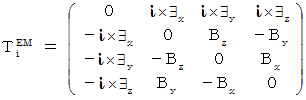
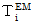 is the tensor which elements of
is the tensor which elements of  Electromagnetic field antisymmetric contravariant tensor
Electromagnetic field antisymmetric contravariant tensor in the first column or the first row are replaced with imaginary number.
in the first column or the first row are replaced with imaginary number.  Four-dimensional electromagnetic force
Four-dimensional electromagnetic force 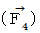
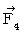
 is expressed as follows with
is expressed as follows with  complex number electromagnetic field tensor.
complex number electromagnetic field tensor. 
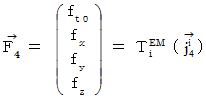
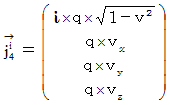
 complex number four-dimensional
complex number four-dimensional
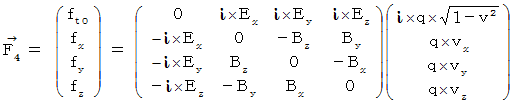
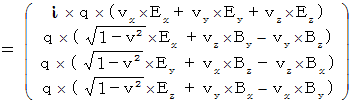
 ) that the object A exerts an influence on the object B is obtained as follows by making
) that the object A exerts an influence on the object B is obtained as follows by making  Electromagnetic field antisymmetric covariant tensor
Electromagnetic field antisymmetric covariant tensor 
 exert an influence on
exert an influence on  Four-dimensional space-time electric current.
Four-dimensional space-time electric current.  :
: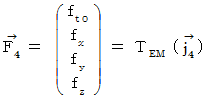
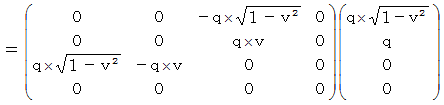
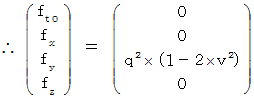
 ) on the space-time
) on the space-time  of the 0th observer's coordinate system. We obtain it with the same way as above-mentioned.
of the 0th observer's coordinate system. We obtain it with the same way as above-mentioned.
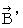 ) on the space-time point
) on the space-time point  of the 0th observer's coordinate system. It is
of the 0th observer's coordinate system. It is  .
. four-dimensional electromagnetic force
four-dimensional electromagnetic force 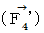
 that the object A exerts an influence on the object B with respect to the 0th observer is as follows :
that the object A exerts an influence on the object B with respect to the 0th observer is as follows :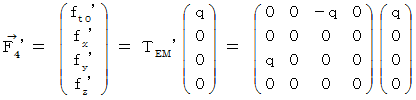
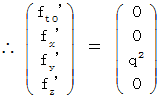
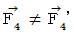 . That is, we find that the electromagnetic force that the object A exerts an influence on the object B changes due to a coordinate conversion. Actually, it was hoped that the hypotheses make the force constant regardless of a coordinate conversion and hold 'principle of relativity' good. But, it's a pity that it disappointed our expectations. If the force between two conductors with the same direction of electric current would be not attraction but counter attraction, everything goes well. Actually, it is attraction.
. That is, we find that the electromagnetic force that the object A exerts an influence on the object B changes due to a coordinate conversion. Actually, it was hoped that the hypotheses make the force constant regardless of a coordinate conversion and hold 'principle of relativity' good. But, it's a pity that it disappointed our expectations. If the force between two conductors with the same direction of electric current would be not attraction but counter attraction, everything goes well. Actually, it is attraction.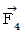 and
and 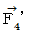 with
with  Electromagnetic field antisymmetric contravariant tensor.
Electromagnetic field antisymmetric contravariant tensor. 
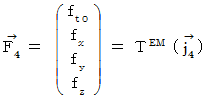
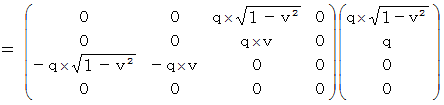
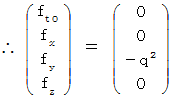
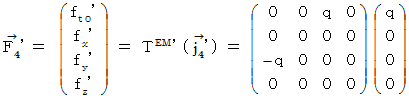
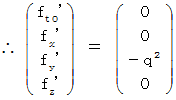
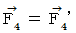 . But, it looks strange. Why it is
. But, it looks strange. Why it is 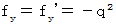 instead of
instead of 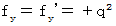 ? If it is
? If it is 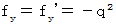 , the force between electric charges with the same number becomes attraction; it is repulsive force actually. Therefore, this method did not make it, too.
, the force between electric charges with the same number becomes attraction; it is repulsive force actually. Therefore, this method did not make it, too. Complex number electromagnetic field tensor
Complex number electromagnetic field tensor 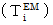
 comes in. Let us find
comes in. Let us find 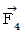 and
and 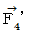 with
with 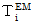 .
.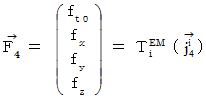
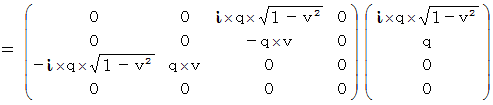
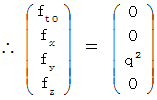
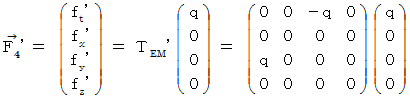
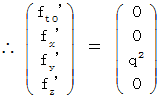
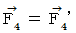 and
and 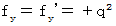 . Then, we feel a whole lot better. I, however, don't feel better. I think that something only
. Then, we feel a whole lot better. I, however, don't feel better. I think that something only  Complex number electromagnetic field tensor
Complex number electromagnetic field tensor 
 can explain is wrong. I don't accept Minkowski's space-time, which accepts imaginary time, as space-time in physics. Therefore, the hypotheses in this corner are all turned down.
can explain is wrong. I don't accept Minkowski's space-time, which accepts imaginary time, as space-time in physics. Therefore, the hypotheses in this corner are all turned down. four-dimensional force
four-dimensional force , because the object produces
, because the object produces  four-dimensional electric current.
four-dimensional electric current.
 Complex number electromagnetic field tensor
Complex number electromagnetic field tensor 
 shows a state of electromagnetic field on one space-time point. It is a antisymmetric matrix with four columns and four rows, and it consists of six kinds of element and the element of 0.
shows a state of electromagnetic field on one space-time point. It is a antisymmetric matrix with four columns and four rows, and it consists of six kinds of element and the element of 0.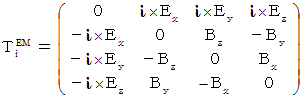
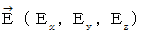 is a substantial electric field.
is a substantial electric field.
 Complex number four-dimensional electromagnetic force
Complex number four-dimensional electromagnetic force  by making
by making  Complex number electromagnetic field tensor
Complex number electromagnetic field tensor  exert an influence on
exert an influence on  Complex number four-dimensional space-time electric current.
Complex number four-dimensional space-time electric current.
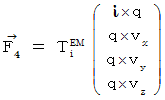
 Complex number electromagnetic field tensor
Complex number electromagnetic field tensor , and it has the following stealthy law :
, and it has the following stealthy law : We obtain
We obtain  Complex number four-dimensional space-time electric current density
Complex number four-dimensional space-time electric current density multiplied by
multiplied by  Electromagnetic transmittance
Electromagnetic transmittance by partial differentiating
by partial differentiating  Complex number electromagnetic field tensor
Complex number electromagnetic field tensor in Minkowski's four-dimensional space-time.
in Minkowski's four-dimensional space-time.
 Complex number electromagnetic field tensor
Complex number electromagnetic field tensor 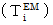
 as follows with elements of
as follows with elements of 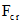 :
: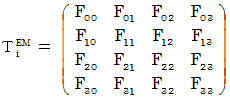
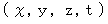 as follows with
as follows with 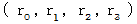 :
: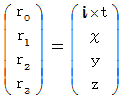
 of complex number electromagnetic field tensor and four-dimensional space-time coordinates
of complex number electromagnetic field tensor and four-dimensional space-time coordinates 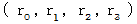 .
.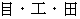 units ) :
units ) : ]
]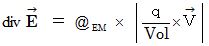
 ]
]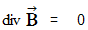
 ]
]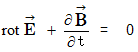
 ]
]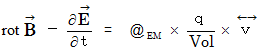
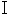 ]
]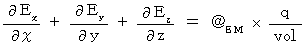
 (Equality 001)
(Equality 001)
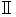 ]
]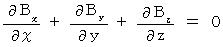
 (Equality 002)
(Equality 002) ]
]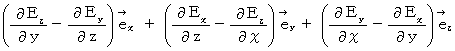
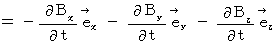
 ]
]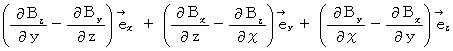
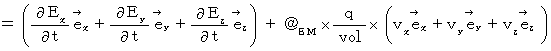
 ] , we obtain the following equalities :
] , we obtain the following equalities :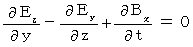
 (Equality 003)
(Equality 003) 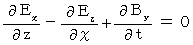
 (Equality 004)
(Equality 004) 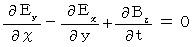
 (Equality 005)
(Equality 005) 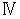 ] , we obtain the following equalities :
] , we obtain the following equalities :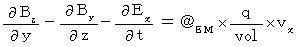
 (Equality 006)
(Equality 006)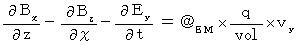
 (Equality 007)
(Equality 007)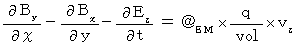
 (Equality 008)
(Equality 008) ] and [ Equation
] and [ Equation  ] .
] .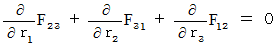
 (Equality 002' )
(Equality 002' )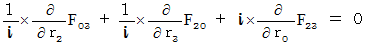
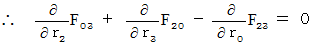
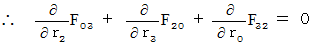
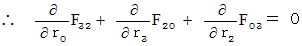
 (Equality 003' )
(Equality 003' )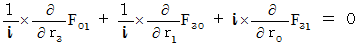
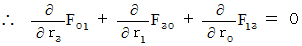
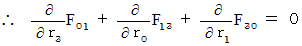
 (Equality 004' )
(Equality 004' ) 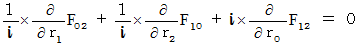
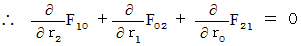
 (Equality 005' )
(Equality 005' ) (Equality 005' ) into the following equality :
(Equality 005' ) into the following equality :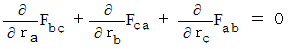
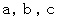 are different integers of
are different integers of 
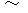
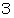 , respectively.
, respectively.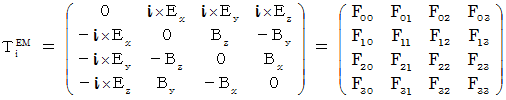
 ] and [ Equation
] and [ Equation 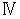 ] .
] .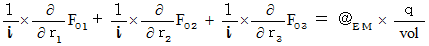
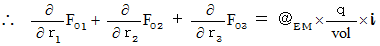
 (Equality 001' )
(Equality 001' )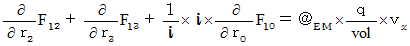
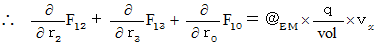
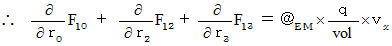
 (Equality 006' )
(Equality 006' )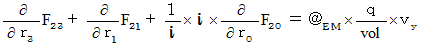
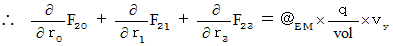
 (Equality 007' )
(Equality 007' )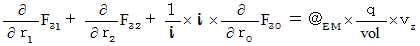
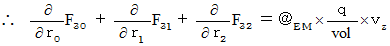
 (Equality 008' )
(Equality 008' ) 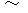 (Equality 008' ) .
(Equality 008' ) .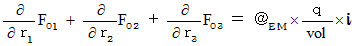
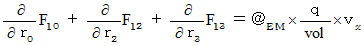
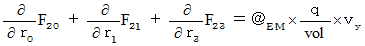
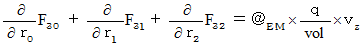
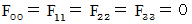 , these four equalities are expressed as follows :
, these four equalities are expressed as follows :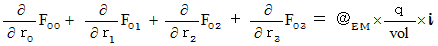
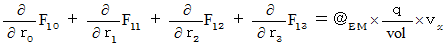
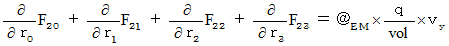
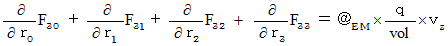


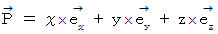
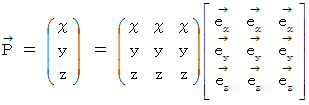
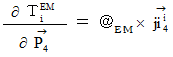
 :
: :
: :
: :
:
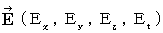
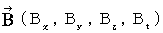
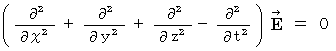

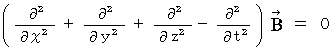

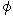

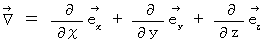
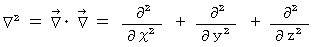
 )
)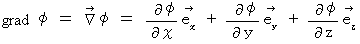
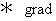 is an operator which changes scalar to vector.
is an operator which changes scalar to vector.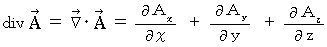
 is an operator which changes vector to scalar.
is an operator which changes vector to scalar.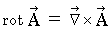
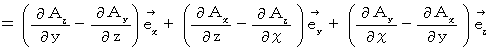
 is an operator which changes vector to vector.
is an operator which changes vector to vector.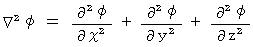
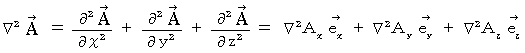
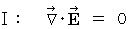

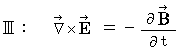
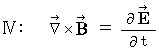
 , we obtain the following equality :
, we obtain the following equality :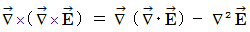
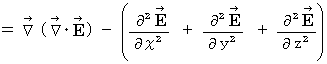
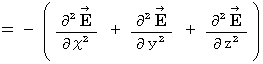

 and
and  , we obtain the following equality :
, we obtain the following equality :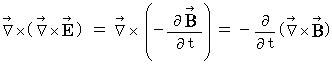
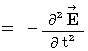

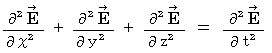
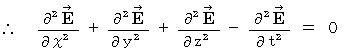
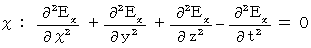
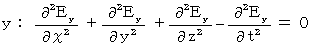
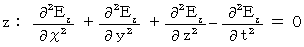
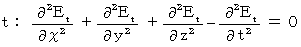
 , we obtain the following equality :
, we obtain the following equality :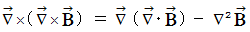
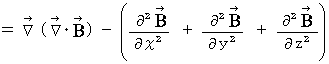
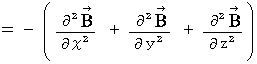

 and
and  , we obtain the following equality :
, we obtain the following equality :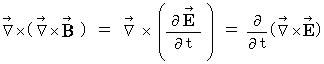
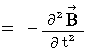

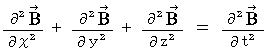
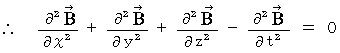
 be a wave function :
be a wave function : 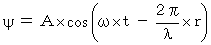
 shows D'Alembert operator :
shows D'Alembert operator :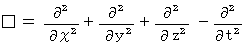
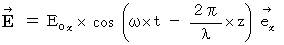
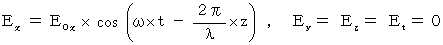
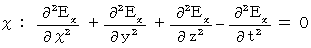
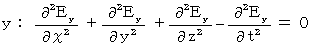
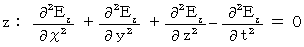
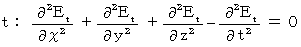
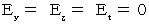
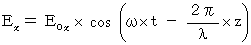 makes
makes 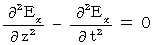 be satisfied.
be satisfied.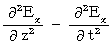
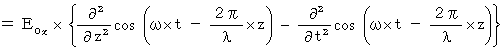
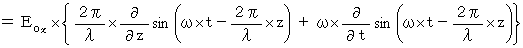
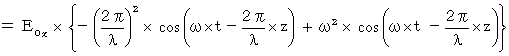
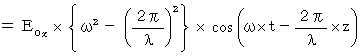
 , we obtain the following equality :
, we obtain the following equality :
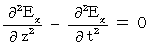
 :
: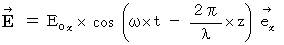
 as follows :
as follows :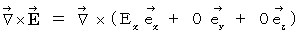

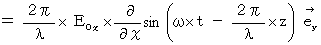
 becomes as follows :
becomes as follows :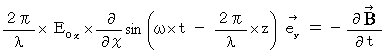
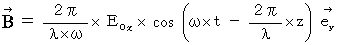
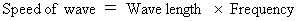 , we obtain the following equality :
, we obtain the following equality :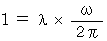
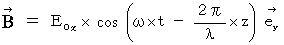
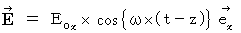
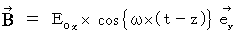
 in the direction of the vector
in the direction of the vector  .
.