Preface
As a study and sports for children must not be forced only for a future success, I want a study for adults to be something to enjoy excitedly seeing the mechanism of nature and the structure of society and to be something to enjoy tastefully understanding person's mind and the wisdom for a life.
I remember discussing the theory of relativity with my friend all night in my college days. Since then, when I have free time, I enjoyed considering some strange problems in the theory of relativity. As time went by, I wanted to write a guidebook of the special theory of relativity for such collage students. At last, this book has made. ( I introduce the digest of this book in this homepage, while revising it further. )
My idea is more or less different from the general interpretation of the theory of relativity. I may misinterpret it a little, because I am a self-educated amateur. Therefore, please read a book written by the specialist at the same time. Please excuse me for describing many laws made without permission in this book, because it is a way of expressing my view well.
It is difficult to describe physics involving movements of objects moving regardless of human's will, by using only words from a life of human. Therefore, we use figures and equalities. A physical term, however, must be used correctly. For example, although in our life the word 'time' is used meaning not only 'period of time' but also 'point in time,' these two meanings must be distinguished clearly in physics. Therefore, I will use the following terms made without permission in this book.
Thank you for your understanding.
 Time
Time --------------
-------------- Time as a concept
Time as a concept
 Time point
Time point ---------
--------- Point in time ; If it says 'time position'
Point in time ; If it says 'time position'
 Time interval
Time interval -------
------- Period of time ; During two time points
Period of time ; During two time points
 Space
Space -------------
------------- Space as a concept ; Not mean universe
Space as a concept ; Not mean universe
 Space point
Space point --------
-------- What is called 'position'
What is called 'position'
 Space interval
Space interval ------
------ What is called 'distance'
What is called 'distance'
All objects are constantly traveling through four-dimensional space-time at the speed of light. Light is traveling through space at the speed of light, and we are traveling through proper time at the speed of light. Moreover, an object traveling through space at 3/5 of the speed of light is also traveling through proper time at 4/5 of the speed of light.
 Note :
Note : (3/5)2 + (4/5)2 = 1
(3/5)2 + (4/5)2 = 1
The difference of movements of an object through proper time and space as follows:
First, although we can travel through space not only in the positive direction but also in the negative direction, we can travel through proper time only in the positive direction. Second, although space is three-dimensions, proper time is one-dimension.
All objects grow older equally. an object grows older not only when it travels through proper time, but also when it travels through space. If we don't recognize this fact, we fit into the trap called 'Twins paradox.' It follows not proper time but time that an object travels, acts, and grows older. We must distinguish exactly 'time' and 'proper time.'
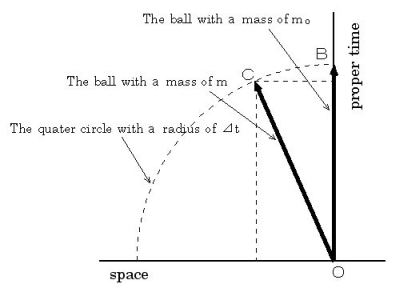
Now, we will study the difference between 'time' and 'proper time.' Please imagine vacuum and weightless universe. Two standardized balls are traveling with liner uniform motion in the same direction at different speed on the same orbite. Two balls are spinning at the same speed. Please consider that two balls don't collide even if they exit on the same space-time point, because of a thought experiment. Just now, the ball of the faster one is overtaking the ball of the slower one. You are in a spaceship moving with the same velocity as the ball of the slower one. You start observation at the very moment the ball of the faster one overtakes the ball of the slower one. We set the 'space-time point' on which the ball of the faster one overtakes the ball of the slower one to be the origin. The movement of two balls for time intervals of d t is expressed by using a four-dimensional space-time coordinate system in Figure 0101.
Figure 0101

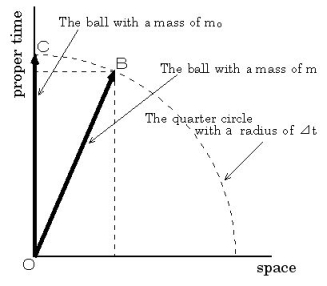
Please notice that 'space' and 'proper time' are set to be the horizontal axis and the vertical axis, respectively. Three-dimensional space is expressed with one-dimension to simplify. Masses of two balls are expressed with 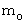 and
and 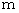 . The magnitudes of two vectors which show the movements of balls are equal. At a time point of d t , the traveling ball and the stationary ball exist on the 'space-time point'
. The magnitudes of two vectors which show the movements of balls are equal. At a time point of d t , the traveling ball and the stationary ball exist on the 'space-time point'  and on the 'space-time point'
and on the 'space-time point'  , respectively.
, respectively.
Note: 'Space-time point' is the point in the four-dimensional space-time coordinate.
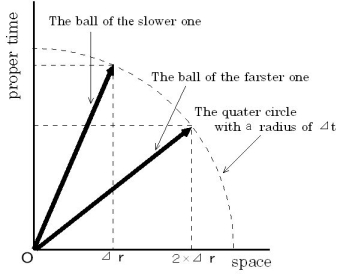
How is this situation observed by your friend in a spaceship moving with the same velocity as the ball of the faster one? The answer is expressed in Figure 0102.
Figure 0102

When we compare Figure 0101 with Figure 0102, we find the following statements:
 a ) The magnitudes of the vectors are constant
a ) The magnitudes of the vectors are constant  .
.
 b ) The masses of two balls are replaced each other.
b ) The masses of two balls are replaced each other.
 c ) The proper time intervals of two balls are replaced each other.
c ) The proper time intervals of two balls are replaced each other.
Therefore, you and your friend say each other as follows:
 I have observed the stationary ball for time intervals of
I have observed the stationary ball for time intervals of  and for proper time intervals of
and for proper time intervals of  .
. 
Then, you and your friend object each other as follows:
 You have observed the stationary ball under your very nose for time intervals of
You have observed the stationary ball under your very nose for time intervals of  . Nevertheres, you have observed it for shorter proper time intervals than
. Nevertheres, you have observed it for shorter proper time intervals than  .
.
Please stop quarreling. Not only what you say but also what your friend says is right. Please listen to me:
 First, 'time' is the magnitude of a vector. Therefore, 'time' is not a vector. 'Proper time' is a vector which has a cirtain direction. Moreover, 'proper time' is one of axes of four-dimensional space-time coordinate system; these axes intersect perpendicularly each other.
First, 'time' is the magnitude of a vector. Therefore, 'time' is not a vector. 'Proper time' is a vector which has a cirtain direction. Moreover, 'proper time' is one of axes of four-dimensional space-time coordinate system; these axes intersect perpendicularly each other.
Second, 'time' is an absolute one which acts as a parameter to determine a space-time point on which a traveling object exists. 'Proper time' is a relative time which changes in length as a result of a kinetic relationship between an observer and an observed object.
Therefore, I call time 'absolute-time' and call proper time 'relative-time.'
Last, please notice the following statement:
 Both absolute-time intervals and relative-time intervals must be measured with the same ruler. That is, the length of unit absolute-time interval is equal to the lngth of unit relative-time interval.
Both absolute-time intervals and relative-time intervals must be measured with the same ruler. That is, the length of unit absolute-time interval is equal to the lngth of unit relative-time interval.


Now, please return to Figure 0101. Then, we have your friend fly with a velocity which magnetude is the same as that of the ball of the faster one with respect to your spaceship and which direction is opposite to the direction of the ball of the faster one with respect to your spaceship. I show the movements of two balls with respect to your friend in Figure 0103.
Figure 0103

Oh! I am sorry. Please wait just for a moment. There is something wrong. The mistake is that the speed of the ball of faster one is twice the speed of the ball of slower one. In fact, the speed of the ball of the faster one is slower than twice the speed of the ball of the slower one. That is, simple addition is not accepted on a composition of speeds. I will describe in Chapter 7 for details.
Well we return to Figure 0101 again. Oh! In the meantime, one ball has gone ahead. So, please hit the stationary ball under your nose with a bad to make two balls collide. And then please express this situation with Figure.
Figure 0106

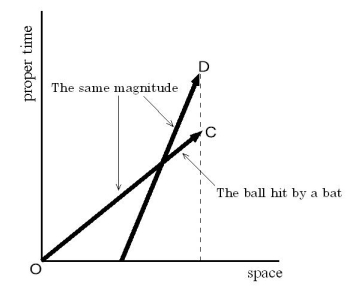
Good job! On one hand, for the ball hit by the bad, the space-time point on which two balls collide is the space-time point  , on the other hand, for the ball flying ahead, the space-time point on which two balls collide is the space-time point
, on the other hand, for the ball flying ahead, the space-time point on which two balls collide is the space-time point 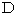 .
.
Therefore, we see the following statement:
 The nesessary condition of a collision of objects is an accordance of 'absolute-time points' of objects and an accordance of 'space points' of objects. An accordance of 'relative-time points' of objects is not nessesary for a collision of objects.
The nesessary condition of a collision of objects is an accordance of 'absolute-time points' of objects and an accordance of 'space points' of objects. An accordance of 'relative-time points' of objects is not nessesary for a collision of objects.
 Main page
Main page
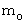 and
and 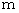 . The magnitudes of two vectors which show the movements of balls are equal. At a time point of d t , the traveling ball and the stationary ball exist on the 'space-time point'
. The magnitudes of two vectors which show the movements of balls are equal. At a time point of d t , the traveling ball and the stationary ball exist on the 'space-time point'  and on the 'space-time point'
and on the 'space-time point' 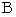 , respectively.
, respectively.
 .
. I have observed the stationary ball for time intervals of
I have observed the stationary ball for time intervals of 
 Both absolute-time intervals and relative-time intervals must be measured with the same ruler. That is, the length of unit absolute-time interval is equal to the lngth of unit relative-time interval.
Both absolute-time intervals and relative-time intervals must be measured with the same ruler. That is, the length of unit absolute-time interval is equal to the lngth of unit relative-time interval.


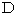 .
.