第2章 相対時間( 固有時間 )の本当の役割とは何か?
相対時間( 固有時間 )は、「 次元的相対的幻影的時間 」に甘んじてはいません。 それは、「 光の周波数 」や「 質量 」や「 垂直方向の物質の速さ 」や「 クーロン力 」を決定する重要な役割をしているのです。また 図0101 に戻って、 話を再開することにします。 さて、 ここで問題です。 2つのボールの相対時間( 固有時間 )の大きさがどの程度異なっているのかを観測するには、 どうすればいいでしょうか? そうですね、 ボールの代わりに時計を飛ばしてやればいいのです。 では、思い浮かべてください。 無重力宇宙空間の同一平面上を2つの同じ規格の時計が同じ方向に異なる速さで、 それぞれ等速直線運動しています。 あなたは宇宙船に乗って、 2つの時計の運動ラインの真ん中より少しだけ速い方の 時計
 に近いラインを遅い方の 時計
に近いラインを遅い方の 時計  と同じ速度で並んで飛んでいます。 そして、 もうすぐ 時計
と同じ速度で並んで飛んでいます。 そして、 もうすぐ 時計  に追い越されようとしています。 観察はここから始まります。 図0201 を見てください。
に追い越されようとしています。 観察はここから始まります。 図0201 を見てください。図0201
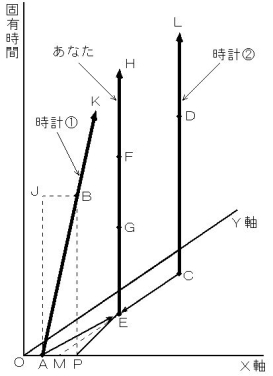
まず、 あなたは、 時計
 がA時空点にさしかかった時の 時計
がA時空点にさしかかった時の 時計  の時刻 と 時計
の時刻 と 時計  の時刻を、 同時に測定してください。 その次に、 時計
の時刻を、 同時に測定してください。 その次に、 時計 がB時空点にさしかかった時の 時計
がB時空点にさしかかった時の 時計  の時刻 と 時計
の時刻 と 時計  の時刻を、 同時に測定してください。 そして、 その差を比較すれば、 2つの相対時間( 固有時間 )の差がわかります。 しかし、 ここで1つ注意しておかなければならないことがあります。 それは、 あなたが、 時空点Aに存在するときの 時計
の時刻を、 同時に測定してください。 そして、 その差を比較すれば、 2つの相対時間( 固有時間 )の差がわかります。 しかし、 ここで1つ注意しておかなければならないことがあります。 それは、 あなたが、 時空点Aに存在するときの 時計  の時刻 と 時空点Cに存在するときの 時計
の時刻 と 時空点Cに存在するときの 時計  の時刻 を同時に測定する時空点は、 点Eではなくて点Gであるということです。 なぜならば、 あなたが時計の時刻を観測できるのは、 光のおかげであり、 時計とあなたが離れているぶんだけ、 光が届くのに時間がかかるからです。
の時刻 を同時に測定する時空点は、 点Eではなくて点Gであるということです。 なぜならば、 あなたが時計の時刻を観測できるのは、 光のおかげであり、 時計とあなたが離れているぶんだけ、 光が届くのに時間がかかるからです。さあ観測の結果はどうでしたか? なんと、 差はゼロです! いったいこれはどうしたことでしょう? それは、 相対時間( 固有時間 )に差がないのか、 観測の方法が間違っていたのかのどちらかです。 その答えは、 後者のほうです。 つまり観測方法の発想はよかったのですが、 時計が相対時間をちゃんと測定できる物差しであると思ってしまったところに間違いがあったのです。
では、 どうすれば2つのボールの相対時間の大きさの差を観測することができるのでしょうか? 実は、 光を使えば観測することができるのです。「 光源内で発生する光子の電磁波的振動は、 どんな観察のされ方をしても、 単位絶対時間あたりの振動数、 つまり、 振動の速さは、 一定であり、 その相対時間方向の振動だけが、 空間に光の速さで伝わって行く。」という性質がありますが、 それを利用するのです。 つまり、 伝わってきた光の振動数は、 ドップラー効果が無ければ、 光源内の光子の相対時間方向の電磁波的振動数と同じなのです。
図0202 を見てください。 光子の電磁波的振動は、 振動する光子の容器である光源の空間移動によって、 相対時間方向へ実現されるだけでなく、 空間方向へも実現され、 その相対時間方向の振動だけが、 空間に光の速さで伝わって行くのです。 ですから、 光源が空間を移動する程度が大きければ大きい程、 その間の相対時間が短くなりますので、 相対時間方向の振動数は少なくなり、 空間を伝わってくる光の振動数は、 少なくなります。
図0202
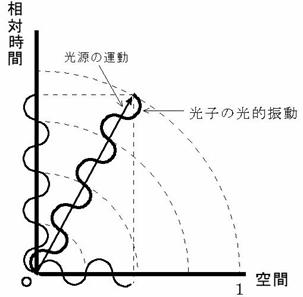
さあ、 話を元に戻しましょう。 もう一度、 図0201 を見てください。 そして、 2つの時計の代わりに、 光源が静止している時に単位絶対時間あたりの振動数( 周波数 )ν の光を放つ2つの光源が運動していると考えてください。 相対時間方向の振動だけが、 空間に光として伝わって行きますので、 運動している光源から放たれた光の振動数は、 静止している光源から放たれた光の振動数よりも、 絶対時間に対する相対時間の割合と同じ程度少なくなっています。 ということは、 光の速さは一定ですので、 運動している光源が放つ光の波長は、 静止している光源の放つ光の波長に比べて長くなっています。
* 周波数 × 波長 = 波の伝播する速さ
この事実は、 実験で検証されており 、一般には「 横ドップラー効果 」と言われていますが、 私はこの現象はドップラー効果ではないと考えていますので、 これを「 光子の電磁波的振動の法則 による、 光の波長の伸び。」と言っています。
相対時間( 固有時間 )の役割が、 だんだんと見えてきましたね。 では、 さらに理解を深めていきましょう。 また最初の 図0101 に戻ってください。 そして、 2つのボールの質量 m と m 0 の違いに注目してください。 また、 2つのボールがそれぞれ同じ速さでスピン( 自転 )しながら飛んでいることを思い出してください。 はい、 それが終わったら、 また思い浮かべていただきます。 今、 幼稚園で2人のお友達が、 自分のバケツに入っている水の量を測っています。 それぞれのコップで自分のバケツの水をすくって、 何杯あるのか調べています。ゆきちゃんのコップは大きくて、 まいちゃんのコップの2倍の容量があります。 その結果、 ゆきちゃんはちょうど3杯で、 まいちゃんはちょうど6杯でした。 そこで、 まいちゃんが言いました。 「 ゆきちゃんのバケツの中のお水の量は、 まいちゃんのちょうど半分ね。」 すると、ゆきちゃんが応えます。「 そうね。そうね。」 なんともほほえましいお話ですね。 本当はバケツの中の水の量は同じなのにね。 しかし、 実は、 自然界では、 この2人の勘違いが正しいという場合があるのです。 どういう場合かと言いますと、 次の

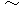
 のように置き換えた場合です。
のように置き換えた場合です。 バケツの中の水の容量 ⇒ ある長さの絶対時間における物質の総スピン数
バケツの中の水の容量 ⇒ ある長さの絶対時間における物質の総スピン数 コップの容量 ⇒ その長さの絶対時間中に経過する相対時間の長さ
コップの容量 ⇒ その長さの絶対時間中に経過する相対時間の長さ 測定された杯数 ⇒ 観測される物質の単位相対時間あたりのスピン数
測定された杯数 ⇒ 観測される物質の単位相対時間あたりのスピン数上記の例では、 ゆきちゃんは静止していて、 まいちゃんは運動していると考えてください。 したがって、 ゆきちゃんの「 ある長さの絶対時間中に経過する相対時間の長さ 」は、 その長さの絶対時間に等しくなっています。 一方、 まいちゃんは運動しているので相対時間はそれよりも短くなっているのです。 つまり、 ゆきちゃんから見ると、 まいちゃんのコップは、 まいちゃんが思っているほどに大きくはありません。 たとえば、 ゆきちゃんの半分の長さの相対時間のまいちゃんが観測する物質の単位相対時間あたりのスピン数は、ゆきちゃんに比べて2倍になっています。 ここで、 「 観測される物質の単位相対時間あたりのスピン数とは、観測される物質の質量である。」 と考えてください。 質量とは、 物質の持つ総エネルギーの大きさを表すものです。 運動する物質の質量は、 静止している時よりも大きくなっています。 なぜなら、 運動エネルギーが加わっているからです。 物質は、 観察のされ方次第で静止したりも運動したりもします。 ですから、 観察のされ方次第で、 物質の質量は変わってくるのです。
バケツの中の水の量 ÷ コップの容量 = 杯数
↓↓
物質のスピン数 ÷ 相対時間 = 質量
第3章 光の速さを1とする新しい単位系の提唱
(1) 新しい単位系の提唱人間は、 生活の中から、 自分たちの都合に合わせて、 単位を設定しました。 しかし、 物理学を簡単にするためには、 自然の都合に合わせた単位に変えるべきです。
そこで、 次のように単位を変更してはいかがでしょうか? と提案します。
距離 :
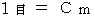
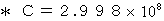 ( 光の速さ )
( 光の速さ )時間 :
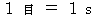
質量 :
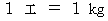
電荷 :
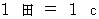
以上、 時間 と 距離 の単位が同じであることが、 新しい単位系の最大の特徴です。 そして、 新しい単位系では、 光の速さが 1 になります。 私は、 この新しい単位系のことを「 目・工・田( もく・こう・でん )単位系 」と言っています。
SI 単位系 の
 などを、 目・工・田 単位系では、 それぞれ、
などを、 目・工・田 単位系では、 それぞれ、 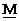 ,
, 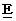 ,
, 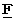 ,
, 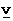 ,
, 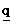 ,
,  などの文字を使って表すことにします。 すると、 次のようになります。
などの文字を使って表すことにします。 すると、 次のようになります。距離 :

時間 :
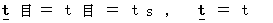
速さ :
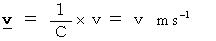
* 新しい単位系では、 速さに単位はありません。
* この式に
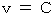 を代入すると、
を代入すると、 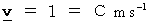
したがって、 新しい単位系では、 光の速さは
 になります。
になります。加速度 :
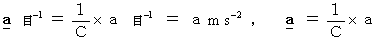
質量 :
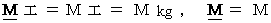
電荷 :

力 :
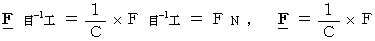
エネルギー :
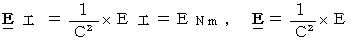
* 新しい単位系では、 エネルギーの単位は質量の単位と同じです。
そして、 新しい単位系では、 力学的 あるいは 電磁気学的 あるいは 相対論的 な法則の方程式が、 次のようになります。
 質量とエネルギーの等価性 :
質量とエネルギーの等価性 : 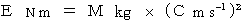 より、
より、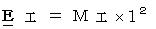
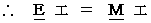 ・ ・ ・ ・ ・(式 3-1)
・ ・ ・ ・ ・(式 3-1)これは、「 質量
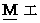 の物質は、
の物質は、 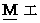 のエネルギーを持っている。」
のエネルギーを持っている。」ことを示します。
 ニュートンの万有引力の法則 :
ニュートンの万有引力の法則 : 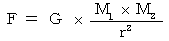 より、
より、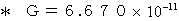 ( 重力定数 )
( 重力定数 )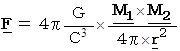 ・ ・ ・ ・ ・(式 3-2)
・ ・ ・ ・ ・(式 3-2)* 私は、(式3-2)の定数
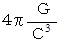 を
を 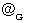 で表すことにしています。
で表すことにしています。* 球の表面積 :
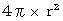
 ローレンツ力 :
ローレンツ力 : 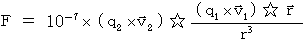
( ☆は外積を表す。) より、
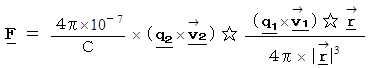
・ ・ ・ ・ ・(式 3-3)
* 私は、(式 3-3)の定数
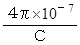 を
を  で表すことにしています。
で表すことにしています。 クーロンの法則 :
クーロンの法則 : 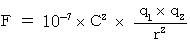 の本当の姿は次式である。
の本当の姿は次式である。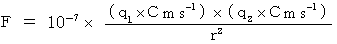
* その理由は、 第20章で述べることにします。
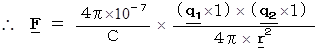 ・ ・ ・ ・ ・(式 3-4)
・ ・ ・ ・ ・(式 3-4)* (式 3-4)の定数は、(式 3-3)と同じ
 です。
です。 新しい単位系では、 ローレンツ変換 は次のようになる。
新しい単位系では、 ローレンツ変換 は次のようになる。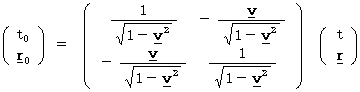
 新しい単位系では、 Maxwellの方程式 は次のようになる。
新しい単位系では、 Maxwellの方程式 は次のようになる。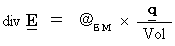
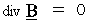
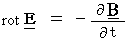
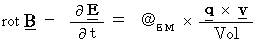
ただし、
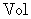 は、 電荷量が占める空間の体積
は、 電荷量が占める空間の体積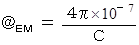
* 私は、
 を「 真空透磁率 」と言わずに、
を「 真空透磁率 」と言わずに、「 透電磁率 」と言っています。
今後は、 目・工・田 単位系 を用いて物理式を記述させていただきます。
また、
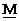 や
や 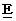 や
や 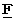 や
や 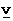 や
や 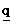 などは、 普通の
などは、 普通の 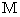 や
や 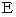 や
や  や
や  や
や 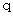 などの文字を使わせていただきます。
などの文字を使わせていただきます。(2) 目工田単位系における物理量の単位
1. 3大基本物理量の名称の提言
時空間 :
 (
( 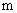 または
または 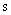 )
)エネマス :
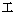 (
( 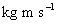 )=(
)=( 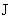 )=(
)=( 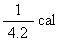 )
)電荷量 :
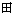 (
( 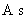 )
)コメント :
・ 「 時点 」や「 空点 」は「 数直線 」上の点です。「 時間 」や「 空間 」は2つ
の点の差であり、「 物理量 」です。
・( )内は、 SI 単位です。
・ 温度(
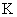 )、 光度(
)、 光度(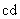 )、 物質量(
)、 物質量(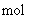 )も 基本単位 です。
)も 基本単位 です。・ 物理量の単位は、 基本単位の組み合わせで表現できます。 基本単位の組み合
わせで表現した単位を、 物理量の 次元 と言います。
2. 次元の指数の合計が
 の物理量( 基本物理量 以外 )
の物理量( 基本物理量 以外 )運動量 :
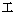 (
( 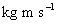 )
)3. 無次元無単位の物理量( 厳密に言うと、 ある基本物理量の比率 )
速度 : (
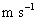 )
)4. 次元の指数の合計が
 の物理量
の物理量電流 :
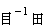 (
( 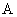 )
)力 :
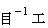 (
( 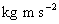 )
)仕事率 :
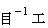 (
( 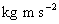 )=(
)=( 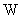 )
)5. 次元の指数の合計が
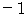 の物理量
の物理量加速度 :
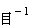 (
( 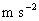 )
)角振動数 :
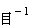 (
( 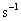 )
)電磁場 :
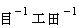 (
( 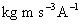 )
)6. 4大物理定数の次元
 ( 電磁波の速さ ): 無単位
( 電磁波の速さ ): 無単位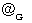 ( 万有引力定数 ):
( 万有引力定数 ): 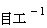
 ( 透電磁率 ):
( 透電磁率 ): 
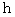 ( プランク定数 ):
( プランク定数 ): 
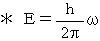

7.
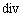 や
や 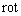 による次元の変化
による次元の変化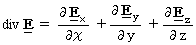
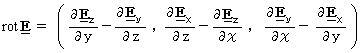
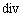 は、 ベクトル から スカラー を取り出す演算子( 関数 )です。 得られるスカラーは、 微小空間内でのベクトルの湧き出し量を表します。 電磁場に演算子
は、 ベクトル から スカラー を取り出す演算子( 関数 )です。 得られるスカラーは、 微小空間内でのベクトルの湧き出し量を表します。 電磁場に演算子 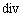 を作用させると、 その次元は、
を作用させると、 その次元は、 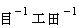 から
から 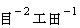 に変化します。
に変化します。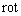 は、 ベクトル を 他のベクトル に変換する演算子です。 得られるベクトルは、 微小空間内のすべてのベクトルの流れによって生じる歯車を回す力のモーメントを表します。 電磁場に演算子
は、 ベクトル を 他のベクトル に変換する演算子です。 得られるベクトルは、 微小空間内のすべてのベクトルの流れによって生じる歯車を回す力のモーメントを表します。 電磁場に演算子 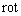 を作用させると、 その>次元は、
を作用させると、 その>次元は、 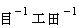 から
から 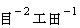 に変化します。
に変化します。
第4章 ローレンツ変換
特殊相対性理論の源泉は、 ローレンツ変換にあります。 そのローレンツ変換の発想原点は、「 真空中の光の速さは、どんな慣性系においても一定である。」という公理です。図0401 を見て下さい。 相対的静止系である3次元空間
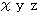 と 速さ
と 速さ  の相対的等速運動系である3次元空間
の相対的等速運動系である3次元空間 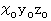 が ちょうど重なった時刻に、 原点から放出された光が、 それぞれの空間でどのように伝わっていくのかを考えます。 ここで、 3次元空間
が ちょうど重なった時刻に、 原点から放出された光が、 それぞれの空間でどのように伝わっていくのかを考えます。 ここで、 3次元空間 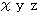 は、時間
は、時間  をパラメーターとし、 3次元空間
をパラメーターとし、 3次元空間  は、 時間
は、 時間  をパラメーターとしています。
をパラメーターとしています。図0401
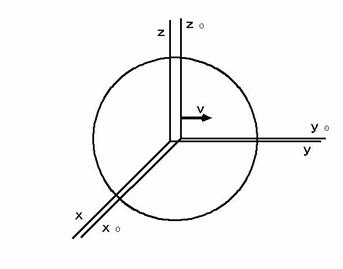
光の速さは 1 で一定ですから、 光の球波面の方程式は、 2つの系でそれぞれ次のように表わされます。
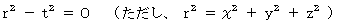

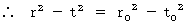 ・ ・ ・ ・ ・ ・(式 4-1)
・ ・ ・ ・ ・ ・(式 4-1)ここで、
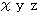
 系
系 
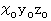
 系 の座標変換を考えます。 簡便にするために、 3次元空間を1次元とし、
系 の座標変換を考えます。 簡便にするために、 3次元空間を1次元とし、 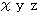 系 の空間を
系 の空間を  で表し、
で表し、 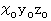 系 の空間を
系 の空間を  で表すことにします。 すると、 線形ベクトル関数( テンソル )を用いて、
で表すことにします。 すると、 線形ベクトル関数( テンソル )を用いて、 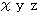
 系
系 
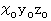
 系 の座標変換は次のように記述できます。
系 の座標変換は次のように記述できます。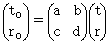 ・ ・ ・ ・(式 4-2)
・ ・ ・ ・(式 4-2)すると、
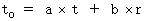 ・ ・ ・ ・ ・(式 4-3)
・ ・ ・ ・ ・(式 4-3)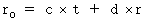 ・ ・ ・ ・ ・(式 4-4)
・ ・ ・ ・ ・(式 4-4)(式 4-3)と(式 4-4)を(式 4-1)に代入して、 変形すると、
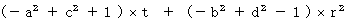
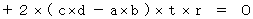
この式が、
 と
と  について恒等式になるための必要条件は、
について恒等式になるための必要条件は、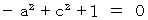 かつ、
かつ、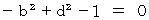 かつ、
かつ、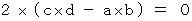 です。
です。これらから、
 ,
, 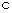 ,
, 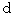 は、
は、  を用いて表すことができますので、(式 4-2)は次のように表されます。
を用いて表すことができますので、(式 4-2)は次のように表されます。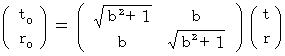 ・ ・ ・ ・ ・(式 4-5)
・ ・ ・ ・ ・(式 4-5)さて、 ここで問題です。

 系 の原点の運動は、
系 の原点の運動は、 
 系 ではどう表されるでしょうか?
系 ではどう表されるでしょうか?答えは、
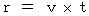 です。
です。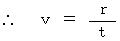 ・ ・ ・ ・ ・(式 4-6)
・ ・ ・ ・ ・(式 4-6)次に、

 系 のどの時空点が、
系 のどの時空点が、 
 系の原点に座標変換されるのか、 考えてみましょう。 まず、(式 4-5)に
系の原点に座標変換されるのか、 考えてみましょう。 まず、(式 4-5)に 
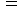
 を代入すると、 次のようになります。
を代入すると、 次のようになります。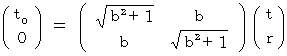
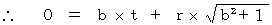
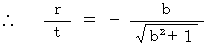 ・ ・ ・ ・(式 4-7)
・ ・ ・ ・(式 4-7)では、(式 4-7)の意味は何でしょうか? それは、

 系 の時空点
系 の時空点 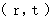 がこの式を満足する時、 座標変換をされると
がこの式を満足する時、 座標変換をされると 
 系 の原点になるということです。
系 の原点になるということです。そこで、

 系の原点を表している(式 4-6)と(式 4-7)を重ねてみます。 すると、
系の原点を表している(式 4-6)と(式 4-7)を重ねてみます。 すると、「(式 4-6)を満たすどんな

 系 の時空点
系 の時空点 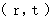 のペアも、(式 4-7)を満たさなければならない。」ということになります。 そのためには、 次の式が成り立たなくてはなりません。
のペアも、(式 4-7)を満たさなければならない。」ということになります。 そのためには、 次の式が成り立たなくてはなりません。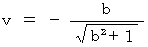
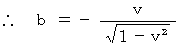 ・ ・ ・ ・(式 4-8)
・ ・ ・ ・(式 4-8)(式 4-8)を(式 4-5)に代入すると、 次のローレンツ変換の式が得られます。
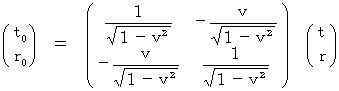 ・・・(式 4-9)
・・・(式 4-9)このローレンツ変換の式:(式 4-9)を逆変換すると、 次の行列式ができあがります。
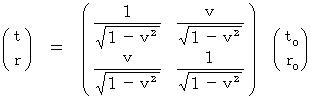 ・・・(式 4-10)
・・・(式 4-10)通常のローレンツ変換の式は(式 4-9)です。 しかし、 私は、 大切なのは、 その逆変換である(式 4-10)だと思っているのです。 ですから、 わざわざ、 この式を、「 逆ローレンツ変換 」と呼んで、 通常のローレンツ変換の式と区別しているのです。
では、 なぜ「 逆ローレンツ変換 」のほうを大切にしなければならないのでしょうか? それは、「 現実は、どう見られるかではなくて、 どう見るか。」だからです。 そして、 逆ローレンツ変換は、 被観察者から観察者への座標変換だからです。
続いて、 もっと簡単な「 ローレンツ変換 」の導き方があるので紹介します。
考えやすくするために、 空間を1次元とします。 静止している座標系
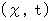 に対して速さ
に対して速さ  で等速直線運動している座標系
で等速直線運動している座標系 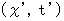 があります。 前者から後者への座標変換式を導くことにします。
があります。 前者から後者への座標変換式を導くことにします。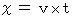 のとき、
のとき、 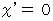 ですから、 空間の座標変換を次のように置くことができます。
ですから、 空間の座標変換を次のように置くことができます。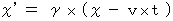 ・ ・ ・ ・ ・ ・(式 4-11)
・ ・ ・ ・ ・ ・(式 4-11)運動の対称性より、(式 4-11)の逆の変換は次のように表されます。
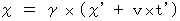 ・ ・ ・ ・ ・ ・(式 4-12)
・ ・ ・ ・ ・ ・(式 4-12)光の伝達の方程式( 光子の移動の方程式 )は、 それぞれの座標系で次のように表されます。
 ・ ・ ・ ・ ・ ・(式 4-13)
・ ・ ・ ・ ・ ・(式 4-13)これから、 光が伝達する時空点について考察します。 光が伝達する時空点たちを、 2次元空間 と 1次元時間 からなる 3次元時空点 で表すと、 ライトコーンになります。 それは、 中の空間は含まれないメガホンのようなものです。 この時空点に限って考察することにします。
(式 4-13)を(式 4-11)と(式 4-12)に代入すると、 次の3つの式が得られます。
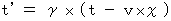 ・ ・ ・ ・ ・ ・(式 4-14)
・ ・ ・ ・ ・ ・(式 4-14)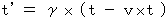 ・ ・ ・ ・ ・ ・(式 4-15)
・ ・ ・ ・ ・ ・(式 4-15)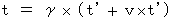 ・ ・ ・ ・ ・ ・(式 4-16)
・ ・ ・ ・ ・ ・(式 4-16)(式 4-15)と(式 4-16)より、
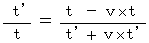
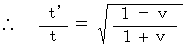
(式 4-15)より、
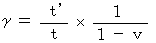
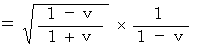
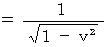 ・ ・ ・ ・ ・ ・(式 4-17)
・ ・ ・ ・ ・ ・(式 4-17)(式 4-17)を(式 4-11)に代入して、
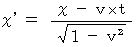 ・ ・ ・ ・ ・ ・(式 4-18)
・ ・ ・ ・ ・ ・(式 4-18)(式 4-17)を(式 4-14)に代入して、
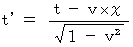 ・ ・ ・ ・ ・ ・(式 4-19)
・ ・ ・ ・ ・ ・(式 4-19)(式 4-18)と(式 4-19)が、 光の伝達路になっている時空点についての座標変換の式です。
ここで、 光の伝達路になっていないすべての時空点についても、(式 4-18)と(式 4-19)が成り立つと仮定します。 すると、(式 4-18)と(式 4-19)は、 静止している座標系
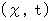 からそれに対して速さ
からそれに対して速さ  で等速直線運動している座標系
で等速直線運動している座標系 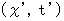 への座標変換を表す式になります。 これらの式をローレンツ変換式と言います。
への座標変換を表す式になります。 これらの式をローレンツ変換式と言います。