��T�́@�@���Ύ��ԂƐ�Ύ��Ԃ̊W
�@ ���₷��Ɩ����Ă���䂪�q�����āA�u ���̎q�͍��ǂ�Ȗ������Ă���̂��낤�H �v�Ǝv�����Ƃ�����܂��B �q�������Ă��閲���A ���A���^�C���Ŏ������邱�Ƃ��ł����Ƃ��Ă��A ����͂����ƁA �q�������Ă��閲�́A ����̂܂܂̎p�ł͂Ȃ��Ǝv���܂��B �ώ@�҂����Ă��镨���A �ʂ̊ώ@�҂��ώ@����ƁA ������������͂ǂ̂悤�Ɍ�����̂ł��傤���H�@����ɓ����Ă����̂��A �t���[�����c�ϊ��Ȃ̂ł��B
�@ �{���ɂ́A ���ꂩ��R��ނ̊ώ@�҂��o�ꂵ�ė��܂��B �܂��A �Î~���Ă��镨���������ώ@����l�ł��B ����� ��O�ώ@�� �ƌĂԂ��Ƃɂ��܂��B ���ɁA �����ȕ����ɂ����ȑ����œ��������^�����Ă��鑽���̑�O�ώ@�ҒB�����Ă��镨�X���ώ@����l�A ����� ��P�ώ@�� �ƌĂԂ��Ƃɂ��܂��B �Ō�ɁA ��P�ώ@�҂ɑ��ē��������^�������Ă���l���A �����̑�O�ώ@�ҒB�����Ă��镨�X���ώ@����ꍇ�ł��B ����� ��Q�ώ@�� �ƌĂԂ��Ƃɂ��܂��B
�@ ���̏͂ł́A ��O�ώ@�҂̊ώ@���e����A ��P�ώ@�҂̊ώ@���e���Ă������Ƃɂ��܂��傤�B ����ɂ́A �����O �� �O�@�ł���Ƃ����������ł̋t���[�����c�ϊ��𗘗p���܂��B
�@ �܂��A�i�� 4-10�j�̋t���[�����c�ϊ���p���āA ���@�Ɓ@���@�̔����ω����ǂ̂悤�ɍ��W�ϊ�����邩���l���邱�Ƃɂ��܂��B ��O�ώ@�҂̍��W�n���i ���O �C ���O �j�A��P�ώ@�҂̍��W�n���i �� �C �� �j�Ƃ��A ����Ȃ� �O �ɋ߂������ω���\���L���Ƃ��� ���i �f���^ �j���g�p���܂��B ����ƁA
�@�@�@�@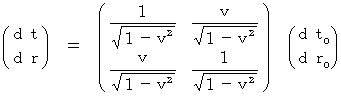 �@�@�@�@�E �E �E �E�i�� 5-1�j
�@�@�@�@�E �E �E �E�i�� 5-1�j
�@ ���������āA�@�i ���� �j�Q �| �i ���� �j�Q�@�� �i �����O �j�Q �| �i �����O �j�Q
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�E �E �E �E �E �E�i�� 5-2�j
�@ �����A ���ꂩ��A ���� �� �̓��������^���n�̒��ŐÎ~���Ă��镨���́A �Î~���Ă��銵���n�ł́A �ǂ̂悤�ɉ^�����Ă��邱�ƂɂȂ�̂��A �l���Ă������Ƃɂ��܂��傤�B �܂�A ��P�ώ@�҂ɑ��đ��� �� �ňړ����Ă����O�ώ@�҂��ώ@���Ă���Î~���Ă��镨�����A ��P�ώ@�҂��ώ@����ǂ̂悤�Ɍ�����̂����A �l���Ă������Ƃɂ��܂��傤�B
�@ ��O�ώ@�҂��ώ@���Ă���Î~���Ă��镨���́A ��Ɂ@�����O �� �O�@�����܂��B
�����O �� �O�@�̎��A�i�� 5-1�j�́A �ȉ��̂Q�̎��ŕ\���܂��B
�@�@�@�@�@�@�@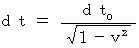 �@�@�@�@�E�E�E�E�E�E�E�E�i�� 5-3�j
�@�@�@�@�E�E�E�E�E�E�E�E�i�� 5-3�j
�@�@�@�@�@�@�@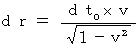 �@�@�@�@�E�E�E�E�E�E�E�E�i�� 5-4�j
�@�@�@�@�E�E�E�E�E�E�E�E�i�� 5-4�j
�@ �����ŁA�i�� 5-3�j���A 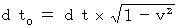 �@������A ������i�� 5-4�j�ɑ�����āA
�@������A ������i�� 5-4�j�ɑ�����āA
�@�@�@�@�@�@�@���� �� ���~�����@�@�ƂȂ�܂��B�@�@�@ �E�E�E�E�E�E�E�i�� 5-5�j
�@ �܂��A�i�� 5-2�j�́A �����O �� �O�@�̎��A ���̂悤�ɕ\�����Ƃ��ł��܂��B
�@�@�@�@�@�@�@�i ���� �j�Q �� �i ���� �j�Q �{ �i �����O �j�Q�@�@�@�@�E�E�E�E�E�E�i�� 5-6�j
�@�i�� 5-3�j�`�i�� 5-6�j���A ��O�ώ@�҂��ώ@���Ă��镨�����A ��O�ώ@�҂ɑ��đ��� �|�� �œ��������^�������Ă����P�ώ@�҂��ώ@����A �ǂ̂悤�Ɍ�����̂��́A �����ł��B
�@ �����A�����Ŗ��ł��B
�@ �����@�́A ���܂��܂ȕ��������܂��܂ȕ����ɂ��܂��܂ȑ����ʼn^�����Ă���̂��ώ@���Ă����P�ώ@�҂̎��Ԃł���A �����O�@�́A �Î~���Ă��镨�������ώ@���Ă����O�ώ@�҂̎��Ԃł��B �ł́A ���������ǂ��炪��ΓI�Ȏ��ԂŁA ���v�̐j��i�߂錹�ɂȂ鎞�ԂȂ̂ł��傤���H
�@ �����́A ��P�ώ@�҂̎��Ԃł��B �ώ@����҂𒆐S�ɂ��āA ���܂��܂ȉ^��������ώ@����镨�X������A ����炪���낢��ɔ�r�����Ƃ����̂��A ���R�E�ł��l�Ԃ̈ӎ��̐��E�ł��A ������O�̂��Ƃł��B�i �@���̐��E�́A���̋t�݂����ł��B�j�@���������āA �����@����ΓI�Ȃ��̂ł���A ��ƂȂ���̂ł��B
�@ ���̂��Ƃ𗝉����Ă��炤���߂ɁA �}0501 �����Ă��������B
����́A�i�� 5-6�j��}�����������̂ł��B ������ �� �A�c���� ���O �ƂȂ��Ă��܂��B �����@�́A���W�i ���� �C �����O �j�̌��_����̋����ɂȂ��Ă��܂��ˁB
�@�@�@
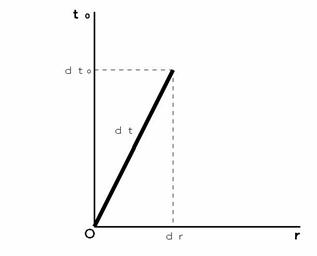
�@ ���ɁA �}0502�����Ă��������B �����@�����̒��ŁA �����@�Ɓ@�����O�@���i�� 5-6�j�̏��������Ȃ���A �ω����Ă����Ă���̂��킩��Ǝv���܂��B
�@ �}0502�@�@�@
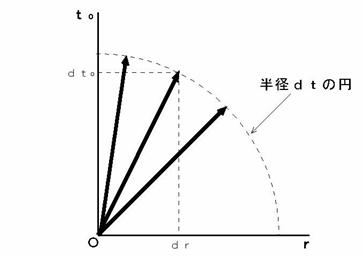
�@ �ώ@����镨�����ώ@�҂ɑ��ĐÎ~���Ă���ꍇ�́A �����@���@�O�@�ƂȂ�A �����̉^���́A ���O ����̃x�N�g���ŕ\����܂��B
�@�i�� 5-6�j�F�i ���� �j�Q �� �i ���� �j�Q �{ �i �����O �j�Q�@ �́A �����O �� �ŗL���ԁi ���Ύ��� �j�Ƃ����A �����@�� ���ԁi ��Ύ��� �j�Ƃ����܂��B �ŗL���� �Ƃ����ƁA �Ȃ��s�ϓI�Ȏ��Ԃ̂悤�Ɏv���܂��̂ŁA ���́A �ŗL���� �̂��Ƃ� ���Ύ��� �ƌ������Ƃɂ��Ă��܂��B
�@ ���Ύ��ԂƂ́A ��P�ώ@�҂��ϑ������O�ώ@�҂̎��Ԃ̂��Ƃł��B �܂�A �Î~���Ă���ώ@�҂ɂ���Ċϑ����ꂽ�A �ώ@���Ă��镨���Ɠ������x�œ��������^�������Ă���ώ@�҂��ʂ蔲���鎞�Ԃ̂��Ƃł��B
�@ ��O�ώ@�҂���P�ώ@�҂ɑ��ĐÎ~���Ă���ꍇ�ɂ́A ���Ύ��Ԃ͐�Ύ��ԂƓ������Ȃ�܂��B ����́A�i�� 5-3�j�� �� �� �O �̏ꍇ�ł���A�i�� 5-6�j�� ���� �� �O �̏ꍇ�ł��B
��U�́@�@�~���R�t�X�L�[����C�v�V���^�C���̂S��������Ԃ�
�@ �O�͂ł́A ��O�ώ@�҂����Ă��镨���A ��P�ώ@�҂��ώ@����ƁA �ǂ̂悤�Ɍ�����̂���T���Ă݂܂����B �ł͍��x�͋t�ɁA ��P�ώ@�҂����Ă��镨���A ��O�ώ@�҂��ώ@����ƁA �ǂ̂悤�Ɍ�����̂����l���Ă݂܂��傤�B ��O�ώ@�҂��ώ@����Ǝ~�܂��Č����邱�Ƃ͊ԈႢ�Ȃ��Ǝv���̂ł��� �E�E�E�E�E�E �B�@ �܂��A �����O �� �O�@�̎��A �t���[�����c�ϊ�����A �����������ꂽ���Ƃ��v���o���Ă��������B�i�� 5-6�j���Čf���܂��B
�@�@�@�@�@�@�i ���� �j�Q�@�� �i ���� �j�Q�@�{�@�i �����O �j�Q
�����ŁA������ �� �ŁA�c���� ���O �̍��W���l���܂��B
������
�@ �R������ԂƑ��Ύ��Ԃ���Ȃ�S��������Ԃ��A ���́u �C�v�V���^�C���̂S��������� �v�ƌ����Ă��܂��B�u �C�v�V���^�C���̂S��������� �v�ɂ́A ���Ɍf����S�̓���������܂��B
�@�@�@
 �@��P�ώ@�҂��ώ@�̎�l���Ƃ��鎞��Ԃł���B
�@��P�ώ@�҂��ώ@�̎�l���Ƃ��鎞��Ԃł���B�@�@�@
 �@�S��������Ԃ́A �R�����̋�ԂƂP�����̑��Ύ��Ԃ��琬�藧���Ă���B
�@�S��������Ԃ́A �R�����̋�ԂƂP�����̑��Ύ��Ԃ��琬�藧���Ă���B�@�@�@
 �@�\�ʓI�ɂ́A ��P�ώ@�Ҍn�Ƒ�O�ώ@�Ҍn�����������S��������ԍ��W�ł���B
�@�\�ʓI�ɂ́A ��P�ώ@�Ҍn�Ƒ�O�ώ@�Ҍn�����������S��������ԍ��W�ł���B�@ �@�@�@�܂�A ��Ԃ͑�P�ώ@�Ҍn�ł���A ���Ԃ͑�O�ώ@�Ҍn�ł���B �������A ���Ԃ�
�@ �@�@�@��O�ώ@�҂����P�ώ@�҂ւ̍��W�ϊ����s����O�̑�O�ώ@�҂̎��Ԃł���B
�@�@�@�@�@�@�������A �����I�ɂ́A ���Ԏ�����P�ώ@�Ҍn�ł���A ���Ԏ��͐��m�ɂ͑��Ύ�
�@ �@�@�@�Ԏ��ł���B
�@�@�@
 �@��Ύ��Ԃ��p�����[�^�[�ɂ��āA �����͐₦������
�@��Ύ��Ԃ��p�����[�^�[�ɂ��āA �����͐₦������  �ŁA ���̂S��������Ԃ�
�ŁA ���̂S��������Ԃ��@ �@�@�@�ړ����Ă���B ���������āA �����̉^����\���O���̓��̂�̒����́A ���̊Ԃ�
�@ �@�@�@��Ύ��Ԃ̒����ɓ������B
�@ �C�v�V���^�C���̂S��������ԍ��W�ł́A �^���̃p�����[�^�[�Ƃ��Ă̐�Ύ��Ԃ̊m�F���s���ł��B �����ŁA ���W�ʒu�Ɛ�Ύ������킩��悤�ɁA ���̂悤�ȕ��@�ŕ\�����Ƃɂ��܂����B
�@�@�@�@�@�@�@�@�@�i�@��ԍ��W �C�@���Ύ��� �C �m ��Ύ��� �n�@�j
�@ �C�v�V���^�C���̎���Ԃ̈��������Ă݂܂��B �l���₷�����邽�߂ɁA ��Ԃ��P�����Ƃ��܂��B �����`�ƕ����a�͏u�ԓI�ɑ��x��ς��邱�Ƃ��ł��A �Q�͏�ɓ��������x�ňړ��i �Î~���܂� �j����Ƃ��܂��B
�@ �ώ@�̊J�n���̂Q�̕��������݂��鎞��_�����̂悤�ɂ��܂��B
�@�@�@�@�@�����` �F�@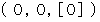 �@�@�@�@�@�@�@�����a �F�@
�@�@�@�@�@�@�@�����a �F�@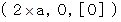
�@ �����āA �Q�̕����́A �ŏ���  �Ɍ����̂U���Ő��̕����Ɉړ����A ����
�Ɍ����̂U���Ő��̕����Ɉړ����A ����  �ɐÎ~���A �Ō��
�ɐÎ~���A �Ō��  �Ɍ����Ő��̕����Ɉړ����܂����B �ώ@���I�������u�Ԃ̂Q�̕��������݂��鎞��_�͎��̂悤�ɂȂ�܂��B
�Ɍ����Ő��̕����Ɉړ����܂����B �ώ@���I�������u�Ԃ̂Q�̕��������݂��鎞��_�͎��̂悤�ɂȂ�܂��B
�@�@�@�@�@�����` �F�@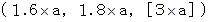
�@�@�@�@�@�����a �F�@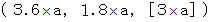
�Q�̕����̈ړ����A �C�v�V���^�C���̎���Ԃ��g���āA ���� �} 0601 �ɕ\���Ă݂܂��B
�@�} 0601
�@�@�@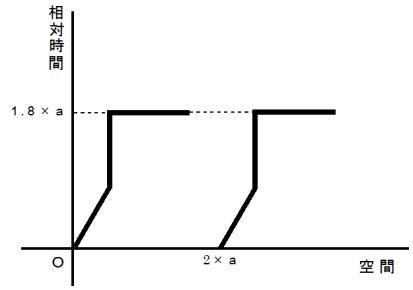
�@ �C�v�V���^�C���̂S��������ԍ��W�ł́A �����̋O�Ղ́u ���̂� �v����Ύ��Ԃ�\���܂��B �������{���ɑ��݂��Ă���ʒu�⎞����\���ɂ́A ��ԍ��W �� ��Ύ��� ���K�v�ł����A ���Ύ����͕K�v����܂���B ���������Ӗ��ł́A�u �C�v�V���^�C���̂S��������Ԃ́A ���z����Ԃł���B�v�ƌ����܂��B
�@ �܂��́A �~���R�t�X�L�[�̎���Ԃ��C���[�W���Ă݂܂��傤�B
�@ �����ŏ㏸����L���G���x�[�^�[�̒��̋�Ԃ��A �Q�̕������قȂ鑬�x�ŏ�ɓ��������^�����Ă���C���[�W�ł��B ���̋�ԑ��x�̑傫���͂O�ȏ�P�ȉ��ł��B �Q�̕����͏u�ԓI�ɑ��x��ύX���邱�Ƃ��ł��܂��B �㏸����G���x�[�^�[�͎��̌o�߂�\���Ă��܂��B �Q�̕��������݂��鎞��_�̐�Ύ��Ԑ����͏�ɓ������ł��B �����ŁA �Q�̕����̏Փ˂��C���[�W�����Ă݂܂��傤�B ����̓G���x�[�^�[���ł̂Q�̕����̏Փ˂̃C���[�W���̂��̂ł��B �܂�A �Փ˂Ƃ́A �Q�̕��������݂��鎞��_�� �w����Ԑ��� �� �x����Ԑ��� �� ��Ύ��Ԑ��� �� ���ׂē������Ȃ��Ă���Ƃ������Ƃł��B
�@ ���ɁA �C�v�V���^�C���̎���Ԃ��C���[�W���Ă݂܂��傤�B
�@ �Q�̕����́A �R��������Ԃ���ɑ��� �P �ňړ����Ă��܂��B �u�ԓI�ɋ�ԑ��x��ς��邱�Ƃ��������Ƃ��Ă��A �R��������Ԃ��ړ����鑬���͏�� �P �ł��B �Q�̕��������݂��鍂���i ���Ύ��Ԑ��� �j�́A �قȂ�ꍇ�̂ق��������ł��B �����ŁA �Q�̕����̏Փ˂��C���[�W�����Ă݂܂��傤�B �Q�̕��������݂��鎞��_�� �w����Ԑ��� �� �x����Ԑ��� �� ��Ύ��ԁi ����͕����̋O�Ղ̒����̑��v�ŕ\����܂��B�j�����ɓ������Ȃ��Ă�������A ���Ύ��Ԑ�������v���Ă��Ȃ��Ƃ��Փ˂ł��B
������
�@ �}�N�X�E�F���������Ƃ́A �d��Ǝ���Ƃ̑��݊W���S�ɂ܂Ƃ߂����̂ł��B �d��Ǝ���Ƃ̑��݊W�͂ǂ�Ȋ����n�ł����藧���܂��B ���̂��Ƃ���A �����w�ɂ�������W�ϊ��̕�������������܂����B ���ꂪ���[�����c�ϊ��ł��B ���W�ϊ��Ƃ́A �ϊ��O�̍��W�n�̎���_���A ����K���ɏ]���āA �ϊ���̎���_�ɂP�P�Ή������邱�Ƃł��B �����͐₦�����W���̎���_����芷���Ȃ���S��������Ԃ��ړ��������Ă��܂��B �ł�����A ���������������w�ɂ����镨���̈ړ��l���̍��W�ϊ��́A ���������݂��鎞��_�̍��W�ϊ��ŕ\����܂��B
�@ �l���₷�����邽�߂ɁA ��Ԃ��w�������̂P�����ł���Ƃ��܂��B �`�N�ɑ��āA�w���̕��̕����ɑ���
 �ňړ����Ă���a�����܂��B �`�N�̍��W�n����a����̍��W�n�ւ̕ϊ��́A ���̎��ŗ^�����܂��B ���̎����A ���́u �t���[�����c�ϊ��� �v�ƌ����Ă��܂��B
�ňړ����Ă���a�����܂��B �`�N�̍��W�n����a����̍��W�n�ւ̕ϊ��́A ���̎��ŗ^�����܂��B ���̎����A ���́u �t���[�����c�ϊ��� �v�ƌ����Ă��܂��B�@�@�@�@�@
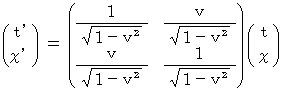
���[�����c�ϊ� ���邢�� �t���[�����c�ϊ��� ���瓱�����̂́A ���̊W���ł��B
�@�@�@�@�@
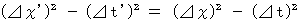
�@ ����́A�u ���Ԃ������Ƃ���S��������ԍ��W�ɂ�����A ���W�ϊ��ɂ��S��������ԋ����s�ς̖@�� �v�ƌ����ׂ����̂ł��B �{���͎��̂悤�ɋL�ڂ������������̂�������܂���B
�@�@�@�@�@
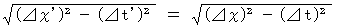
�@ ����́A�u ���W�ϊ��ɂ�����ŗL���ԕs�ς̖@�� �v�������܂��B
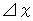 ��
��  �̒l�ɂ���ẮA ���[�g�̒����}�C�i�X�ɂȂ�܂��B ���[�g�̒����v���X�ɂȂ�ꍇ�́u ��ԓI�̈� �v�ƌ����܂��B �܂��A ���[�g�̒����}�C�i�X�ɂȂ�ꍇ�́u ���ԓI�̈� �v�ƌ����܂��B �~���R�t�X�L�[����ŁA ���_��ʉ߂��Ĉړ����镨�������݉\�Ȏ���_��\�������́A ���C�g�R�[���̓����ɂȂ�̈悪�u ���ԓI�̈� �v�ł��B
�̒l�ɂ���ẮA ���[�g�̒����}�C�i�X�ɂȂ�܂��B ���[�g�̒����v���X�ɂȂ�ꍇ�́u ��ԓI�̈� �v�ƌ����܂��B �܂��A ���[�g�̒����}�C�i�X�ɂȂ�ꍇ�́u ���ԓI�̈� �v�ƌ����܂��B �~���R�t�X�L�[����ŁA ���_��ʉ߂��Ĉړ����镨�������݉\�Ȏ���_��\�������́A ���C�g�R�[���̓����ɂȂ�̈悪�u ���ԓI�̈� �v�ł��B�@ �ł͂��ꂩ��A ���ԓI�̈�Ƌ�ԓI�̈�Ƃ̋��E�ɂ�������W�ϊ��̗�����Ă݂܂��傤�B
�@ �`�N�̍��W�n�ɂ����āA ����ʒu�ɑ��݂�����q��
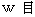 �������Ĉړ������Ƃ��܂��B �܂�A �ώ@�J�n���Ɍ��q�����݂��鎞��_��
�������Ĉړ������Ƃ��܂��B �܂�A �ώ@�J�n���Ɍ��q�����݂��鎞��_�� 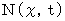 �Ƃ��A �ώ@�I�����Ɍ��q�����݂��鎞��_��
�Ƃ��A �ώ@�I�����Ɍ��q�����݂��鎞��_�� 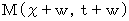 �Ƃ��܂��B ����ƁA ���̎������藧���܂��B
�Ƃ��܂��B ����ƁA ���̎������藧���܂��B�@�@�@�@�@
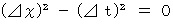
���������āA���̎������藧���܂��B
�@�@�@�@�@
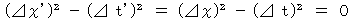 �@�@�@�@�@�E �E �E �E�i �� 6-1�j
�@�@�@�@�@�E �E �E �E�i �� 6-1�j�ł́A ���ۂɎ��̎������藧�̂��ǂ����m���߂Ă݂܂��傤�B
�@�@�@�@�@�@
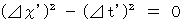
�@ �`�N�̍��W�n�ɂ����� ����_
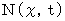 �� ����_
�� ����_ 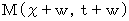 �����ꂼ��a�N�̍��W�n�̎���_�ɕϊ�����ƁA ���̂悤�ɂȂ�܂��B
�����ꂼ��a�N�̍��W�n�̎���_�ɕϊ�����ƁA ���̂悤�ɂȂ�܂��B�@�@�@�@�@����_
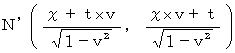
�@�@�@�@�@����_
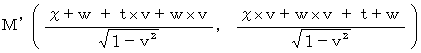
���������āA
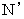 ��
�� 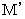 �Ƃ̎���ԋ����̂Q��́A ���̂悤�ɂȂ�܂��B
�Ƃ̎���ԋ����̂Q��́A ���̂悤�ɂȂ�܂��B�@�@�@�@�@
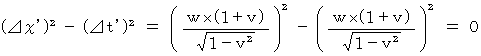
�ȏ�ŁA�m���߂邱�Ƃ��ł��܂����B
�@ �ȏ�̂��Ƃ��������ƊȒP�ɂ��Ă݂܂��B �܂�A ���_����̎���ԋ��������߂�悤�ɂ��Ă��܂��B ���̂��߂ɁA ���̂悤�ɒu�������܂��B
�@�@�@�@�@
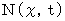 �@�Ɓ@
�@�Ɓ@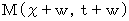 �@�@
�@�@ �@�@
�@�@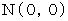 �@�Ɓ@
�@�Ɓ@
����ƁA�i �� 6-1�j�͎��̂悤�ɂȂ�܂��B
�@�@�@�@�@
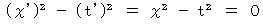 �@�@�@�@�@�E �E �E �E�i �� 6-2�j
�@�@�@�@�@�E �E �E �E�i �� 6-2�j�@ �������A ���̎��͎��_����`���d���g�����݂����鎞��_�ɂ̂����邱���ł��邱�Ƃ�Y��Ȃ��ł��������B
���͎��̂悤�ɍl���Ă��܂��B
�@�@�@�u ���[�����c�ϊ��́A �d����̑��ΐ����������ƂƂ��ɁA �d���g�̓`�d�ɑ�
�@ �@�@���č��W�n�Ԃł̕ϊ���\���B �������A ����͕����̈ړ��ɑ��č��W�n�Ԃł�
�@ �@�@�ϊ���\������ł͂Ȃ��B �ɂ�������炸�A ���[�����c�ϊ��͈ړ����镨���ɑ�
�@ �@�@���Ă��K������Ƃ��Ďg�p����Ă���̂ŁA ���X�̖����������Ă���B�v
�@ �ł͂��ꂩ��A ���̂��Ƃɂ��Đ������܂��B
�i �� 6-2�j�����Ă��������B �`�N�̍��W�n�ɂ����āA ���_��ʉ߂������q�����݂��邱�Ƃ̂ł��鎞��_��
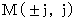 �ƕ\����܂��B �����ŁA ���̂悤�ȍl�������̓��ɕ�����ł��܂����B
�ƕ\����܂��B �����ŁA ���̂悤�ȍl�������̓��ɕ�����ł��܂����B�@�@�@�u ���[�����c�ϊ��́A �}�N�X�E�F���������i �d��Ǝ���Ƃ̑��݊W �j�̑��ΐ�
�@ �@�@�������瓱���o���ꂽ�B �}�N�X�E�F���������̒��� ��_
 �� ���_
�� ���_  �͔C�ӂ�
�͔C�ӂ��@ �@�@
 ��
��  �ł͂Ȃ��A
�ł͂Ȃ��A 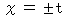 �̊W�����藧�ꍇ��
�̊W�����藧�ꍇ��  ��
��  �ł͂Ȃ��̂��H
�ł͂Ȃ��̂��H�@ �@�@���Ƃ�����A ���[�����c�ϊ��́A �d���g�̓`�d�̍��W�ϊ��ł����āA �����̈ړ�
�@ �@�@�̍��W�ϊ���\���Ă�����̂ł͂Ȃ����ƂɂȂ�B�v
�i �� 6-2 �j�͎��̂悤�ɂ��\����܂��B
�@�@�@�@�@
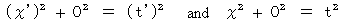
�@ �����ŁA����
 �́A ���q���ړ����鑊�Ύ��Ԃł���ƍl���܂��B�i
�́A ���q���ړ����鑊�Ύ��Ԃł���ƍl���܂��B�i  �ł�������ۂ͈ړ����Ȃ��̂ł��� �j�����āA �����͌��q�ƈ���đ��Ύ��Ԃ��ړ�����ƍl���A �����
�ł�������ۂ͈ړ����Ȃ��̂ł��� �j�����āA �����͌��q�ƈ���đ��Ύ��Ԃ��ړ�����ƍl���A �����  �ƒu���A ���̂悤�Ȏ������肵�܂��B
�ƒu���A ���̂悤�Ȏ������肵�܂��B�@�@�@�@�@
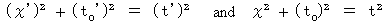
����ɁA ���̂悤�Ȏ������肵�܂��B
�@�@�@�@�@
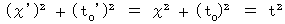
���̉���̎������A ���̑��ΐ����_�̊��Ⴂ�̍��{�ł��B
��V�́@�@���x�̍���
�@ ���̏͂ł́A ��P�ώ@�҂��ώ@���Ă��镨���A ��Q�ώ@�҂��ώ@������A �ǂ̂悤�Ɍ�����̂����l���Ă����܂��B�i�P�j���������̑��x�̍���
�@ �܂��A �����O �� �O�@�̏������ŁA�i�� 5-1�j�́u ��������Ԃ̋t���[�����c�ϊ� �v�ɂ��ϊ����Q��J��Ԃ��Ă��������B ����ƁA ��O�ώ@�҂��ώ@���Ă��镨���Q�ώ@�҂��ώ@����Ƃǂ̂悤�Ɍ����邩���A ���߂邱�Ƃ��ł��܂��B
�@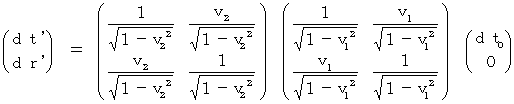
�@�@�@�@�@�@�@
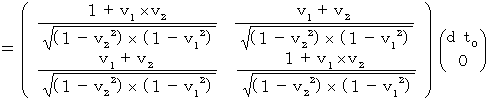
�@�@�@�@�@�@�@
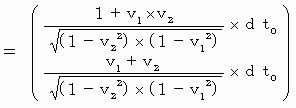
�@ �V�������W�n�Ŋώ@���ꂽ�����̉^���̑����i ���f �j�́A �����f �� �����f�@�ŋ��߂��܂�����A ���̂悤�ɂȂ�܂��B
�@�@�@�@�@�@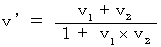 �@�@�@�@�@ �E �E �E �E�i �� 7-1�j
�@�@�@�@�@ �E �E �E �E�i �� 7-1�j
�����s�ς̌����́A ���̂R�̖��肪���ׂĐ^�ł��邱�Ƃ����������̂ł��B
�@�@�@�@�@�ړ����Ă���s�X�g����������ꂽ�e�ۂƈ���āA�ړ����Ă��������������ꂽ
�@�@�@�@���q�́A�����̑��x�̉e����S���Ȃ��B
�@�@�@�A�@�P�̌��q�́A�N���ώ@���Ă�����
 �ňړ����Ă���B
�ňړ����Ă���B�@�@�@�B�@���ׂĂ̌��q�́A����
 �ňړ����Ă���B
�ňړ����Ă���B�@ �͎��̂悤�ɐ��������߂���Ȃ���Ȃ�܂���B
�@�@�@�@�u �ꎟ���ł̑��x�̍����́A�i�� 7-1�j�ŕ\�����Ƃ�������������A ���A �Î~��
�@�@�@�@�Ă������������������q�̑�����
 �ł��邩��A ���q�͌����̑��x�Ɋւ��
�ł��邩��A ���q�͌����̑��x�Ɋւ���@�@�@�@���A ����
 �ňړ�����B�v
�ňړ�����B�v����ɑ��āA ���̂悤�ɍl����̂͊ԈႢ�ł��B
�@�@�@�@�u �e�ۂ͈ړ����Ă���_���������邪�A ���q�͍��W�n�̐Î~���Ă����_�� ��
�@�@�@�@�������B �v
�@ ���̉��߂��ԈႢ�ł��闝�R�́A ���ΐ����_�͌��q�̈ړ��ƕ����̈ړ��ꂳ�������_������ł��B �����A ���̂悤�ɉ��߂��܂��ƁA�u ���[�����c�ϊ��́A ���q�̂ӂ�܂��i �@ �d����I�U���A �A �d���g�I�U���A �B �ŗL���`�d�A �C �ʎq�I���� �j �̎����̂��� �@ �� �B ���瓱���ꂽ���̂Ȃ̂ŁA ���q�Ƃ͉^���̌`�Ԃ��Ⴄ�����̈ړ��Ɋւ��ẮA ���[�����c�ϊ��͓��Ă͂܂�܂���B�v�Ƃ̔��_�ɑ��āA�u �m���ɂ���������ǂ��A ���[�����c�ϊ��������������Ă��A�i ��Ύ��Ԃ����߂��Ă��A�j���q�̈ړ��ƕ����̈ړ��Ƃ͓������ɂȂ��Ă���B�v�ȂǂƔ��_���邱�Ƃ��ł��Ȃ��Ȃ��Ă��܂��܂��B
�@ ���āA �}�C�P���\�� �E ���[���[�̎�����A �A�C���V���^�C���̑��ΐ����_�Ɋւ���ŏ��̘_���̒��ł̃��[�����c�ϊ��̓����́A �܂������s�ς̌������m������O�ŁA�u �����G�[�e����`���A �����̓G�[�e���̊ώ@�҂ɑ��鑬�x�ɂ���ĕω�����B�v�Ƃ����ݒ�ł��̂ŁA ���̒��́u �K�����C�ϊ��ɂ��j���[�g���͊w�I�ȑ��x���� �v�����������ɏo���āA ���ΐ����_��ے肷�邱�Ƃ͊Ԉ���Ă��܂��B
�u ���̓G�[�e����K������
 �œ`���B�v�ƍl����ƁA ���̂��Ƃ��������Ƃ��ł��܂��B
�œ`���B�v�ƍl����ƁA ���̂��Ƃ��������Ƃ��ł��܂��B�@�@
 �F�@ �G�[�e���ɑ��ĐÎ~���Ă���ώ@�҂ɂƂ��ẮA ���̑�����
�F�@ �G�[�e���ɑ��ĐÎ~���Ă���ώ@�҂ɂƂ��ẮA ���̑�����  �ł���B
�ł���B�@�@
 �F�@ �G�[�e���ɑ��đ���
�F�@ �G�[�e���ɑ��đ���  �ňړ����Ă���ώ@�҂ɂƂ��ẮA ���̈ړ��̕����ɓ`��
�ňړ����Ă���ώ@�҂ɂƂ��ẮA ���̈ړ��̕����ɓ`���@ �@�@�@����̑�����
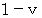 �ł���B
�ł���B�@�@�@�@�@�@�Ȃ��Ȃ�A �Î~���Ă���ώ@�҂ɑ��đ���
 �ňړ����Ă���G�[�e�����A���̋t
�ňړ����Ă���G�[�e�����A���̋t�@ �@�@�@�����Ɍ�������
 �œ`���̂ƁA �������Ƃ�����B
�œ`���̂ƁA �������Ƃ�����B�@�@
 �F�@ �G�[�e���ɑ��ĐÎ~���Ă���`�N�ɂƂ��ẮA �G�[�e���ɑ��đ���
�F�@ �G�[�e���ɑ��ĐÎ~���Ă���`�N�ɂƂ��ẮA �G�[�e���ɑ��đ���  �ňړ�����
�ňړ������@ �@�@�@����a����ɑ���A ���̈ړ��̕����ɓ`�����̑�����
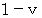 �ł���B
�ł���B�@�@�@�@�@�@�Ȃ��Ȃ�A �`�N�ɂƂ��Ă̌��̑�����
 �ł���A ���A �`�N�ɂƂ��Ă̂a����̑���
�ł���A ���A �`�N�ɂƂ��Ă̂a����̑����@ �@�@�@��
 ������B
������B�@
 ��
��  �̒l�������ɂȂ��Ă��܂��B ���̂悤�ɁA ��ϓI�Ȋώ@�҂ɂƂ��Ă���R�ғI�Ȋώ@�҂ɂƂ��Ă��A �����͕ς��Ȃ��Ƃ����̂��A ���ΐ����_���a������܂ł̃j���[�g���͊w�ł��B
�̒l�������ɂȂ��Ă��܂��B ���̂悤�ɁA ��ϓI�Ȋώ@�҂ɂƂ��Ă���R�ғI�Ȋώ@�҂ɂƂ��Ă��A �����͕ς��Ȃ��Ƃ����̂��A ���ΐ����_���a������܂ł̃j���[�g���͊w�ł��B�������A �����s�ς̌����ɗ����āA ���Θ_�I�ɏ��������Ă݂܂��B
�@�@
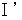 �F�@ ���͔}�̂�K�v�Ƃ����A �ǂ�Ȋώ@�҂ɂƂ��Ă��A�K������
�F�@ ���͔}�̂�K�v�Ƃ����A �ǂ�Ȋώ@�҂ɂƂ��Ă��A�K������  �œ`����Ă���B
�œ`����Ă���B�@�@
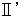 �F�@ �����ɑ��đ���
�F�@ �����ɑ��đ���  �ňړ����Ă���ώ@�҂ɂƂ��ẮA ���̌��������������
�ňړ����Ă���ώ@�҂ɂƂ��ẮA ���̌���������������@ �@�@�@�̑�����
 �ł���B
�ł���B�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���@��������܂������ɉ��������Ă���ώ@�҂̏ꍇ�́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���̎����g���Č��̑��������߂邱�Ƃ��ł��܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
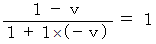
�@�@
 �F�@ �Î~���Ă���`�N�ɂƂ��ẮA �`�N����܂������ɑ���
�F�@ �Î~���Ă���`�N�ɂƂ��ẮA �`�N����܂������ɑ���  �ʼn��������Ă���a�����
�ʼn��������Ă���a������@ �@�@�@����A �`�N�̕�������a����ɓ͂����̑��ΓI�ȑ�����
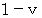 �ł���B
�ł���B�@�u
 �́A ��R�ғI�ȑ��x�ł���A �����s�ς̌�����b�ɂ��Ă��鑊�ΐ����_�ɂ����ẮA �s�v ���� �L�Q �Ȃ��̂ł���B ��R�ғI�ȑ��x�́A ���ΐ����_�����������錶�̑��x�ł����Ȃ��B�v�Ƃ������Ƃɂ��ẮA ��X�� �� ��P�P�� �� ��P�Q�� �ŏq�ׂ邱�Ƃɂ��܂��B
�́A ��R�ғI�ȑ��x�ł���A �����s�ς̌�����b�ɂ��Ă��鑊�ΐ����_�ɂ����ẮA �s�v ���� �L�Q �Ȃ��̂ł���B ��R�ғI�ȑ��x�́A ���ΐ����_�����������錶�̑��x�ł����Ȃ��B�v�Ƃ������Ƃɂ��ẮA ��X�� �� ��P�P�� �� ��P�Q�� �ŏq�ׂ邱�Ƃɂ��܂��B�i�Q�j���������̑��x�̍���
�� �� ��
�@�u �ώ@�҂ɂ܂������ɋ߂Â��Ă���A �܂��́A ���̂��Ă��镨���`����A ���������ɕ����a�������o���ꂽ���A �����a�̐��������̑����́A �����`�Ɠ������x�ʼn^�����Ă���l���������������x���Ȃ�B �Ƃ������Ƃ́A �����`�Ɠ������x�ʼn^�����Ă���l�ɔ�ׂĐ��������̎��Ԃ͂������Ɛi�ނ̂��B�v�Ɨd���������܂��B
�@ �����ŁA ���Ȃ݂ɁA �ނɎ��̂悤�Ȏ�������Ă݂܂��傤�B
�u ���������̎��Ԃ̐i�ݕ��������������ɂȂ�Ƃ����̂́A �[���������܂���B �����Ď��Ԃ͂P�����ł�����ˁB ��������A ���������̋�Ԃ��L�т�ƍl���Ă͂ǂ��ł����H�@���ʂ͓����ł��傤�B�v
�@ ����Ɣނ́A ���������܂��B
�u �n�n�n�n�n�A �����Ȑl�Ԃǂ���B ���O�B�̍l�����ł́A �����܂����̂悤��㩂Ɋׂ��Ă��܂��̂��B �v�������ׂĂ݂��܂��B ���A �Q�̓����T�C�Y�̃����O���݂��Ɍ��������Ȃ���A �������獂���Ŕ��ł��āA ���O�̖ڂ̑O�ŏՓ˂����B �������A������E�̃����O�Ɠ������x�Ŕ��ł����ߓV������A �Q�̃����O�͏Փ˂����ɁA ���̃����O���E�̃����O�̊O��ʂ��Ĕ�ы����Ă��܂��A ���̃����O�Ɠ������x�Ŕ��ł��鈢�C��������A �Q�̃����O�͏Փ˂����ɁA �E�̃����O�����̃����O�̊O��ʂ��Ĕ�ы����Ă��܂��B �ǂ����A �킩�������I�@���O�B�͂����A ����P������ɍ��o���ẮA �ǂ��炩�̃��b�e����\���āA ���낢��Ƌ�ʂ��Ă��邪�A �������� �E �E �E �E�@�v
�@���́A �d���͂��܍��킹�̖��l�Ȃ̂ł��B �����s�ς̌������L�[�v���邽�߂ɂ́A ���������̑��������Ύ��Ԃ̐�Ύ��Ԃɑ���䗦�Ɠ��������Œx���Ȃ�Ȃ���Ȃ�Ȃ����Ƃ��A �ނ͂悭�m���Ă���̂ł��B
�@�i�� 7-4�j�F
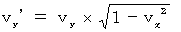 �@�����́u ���ΓI�������x�̖@�� �v�ƌ����Ă��܂��B
�@�����́u ���ΓI�������x�̖@�� �v�ƌ����Ă��܂��B�@ �ł́A ���ꂩ��A�u ���ΓI�������x�̖@�� �v�̍����ɂȂ�v�l���������Ă݂܂��傤�B �v�������ׂĂ��������B ���A ��P�ώ@�҂ɑ��āA �����`������
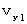 �œ��������^�������Ă��܂��B �����`�́A����
�œ��������^�������Ă��܂��B �����`�́A���� 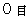 �ɑ�P�ώ@�҂Ɠ����ʒu�ɂ���A �x�������ɉ^�����Ă��܂��B �����`���A ����
�ɑ�P�ώ@�҂Ɠ����ʒu�ɂ���A �x�������ɉ^�����Ă��܂��B �����`���A ���� 
 �̎��̈ʒu��
�̎��̈ʒu�� 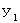 �Ƃ���ƁA ���̎������藧���܂��B
�Ƃ���ƁA ���̎������藧���܂��B�@�@�@�@�@�@
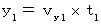 �@�@�@�@�@�E �E �E �E �E�@�i�� 7-5�j
�@�@�@�@�@�E �E �E �E �E�@�i�� 7-5�j�@ ������A �w���̕��̕����ɁA ��P�ώ@�҂ɑ��đ���
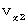 �œ��������^�������Ă����Q�ώ@�҂��ώ@�����Ƃ��ɁA �����`�̉^�������̎������ŕ\���ꂽ�Ƃ��܂��B �������A �Q�l�̎��_�͏d�Ȃ�Ƃ��܂��B
�œ��������^�������Ă����Q�ώ@�҂��ώ@�����Ƃ��ɁA �����`�̉^�������̎������ŕ\���ꂽ�Ƃ��܂��B �������A �Q�l�̎��_�͏d�Ȃ�Ƃ��܂��B�@�@�@�@�@�@
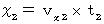 �@�@�@�@�@�@
�@�@�@�@�@�@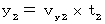
�@ ���̂Ƃ��A�@
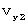 �@���@
�@���@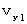 �@�Ɓ@
�@�Ɓ@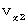 ��p���Ăǂ̂悤�ɕ\����邩�A �l���Ă݂܂��傤�B
��p���Ăǂ̂悤�ɕ\����邩�A �l���Ă݂܂��傤�B��Q�ώ@�҂����P�ώ@�҂ւ̍��W�ϊ��́A ���̃��[�����c�ϊ��ɏ]���܂��B
�@�@�@�@�@�@
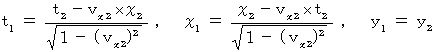
�����̎����i�� 7-5�j�ɑ������ƁA ���̂悤�ɂȂ�܂��B
�@�@�@�@�@�@
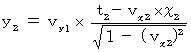
�@�@�@�@�@�@
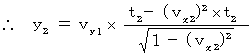
�@�@�@�@�@�@
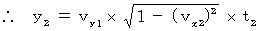
���������āA ���̎������藧���܂��B
�@�@�@�@�@�@
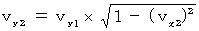
�@ ���̎�����A ��Q�ώ@�҂Ƃ��Ă̕����`�̂x�������̑�����
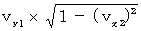 �ł��邱�Ƃ��킩��܂��B ���������āA ��Q�ώ@�҂Ƃ��Ă̕����`�̑���
�ł��邱�Ƃ��킩��܂��B ���������āA ��Q�ώ@�҂Ƃ��Ă̕����`�̑��� 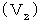 �́A ���̂悤�ɂȂ�܂��B
�́A ���̂悤�ɂȂ�܂��B�@�@�@�@�@�@
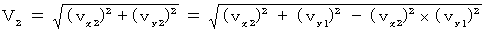
���̎��́A
�@�@
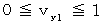 �@���@
�@���@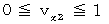 �@�̂Ƃ��A�@
�@�̂Ƃ��A�@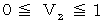 �@�ł��B
�@�ł��B�@�@
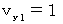 �@�܂��́@
�@�܂��́@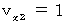 �@�̂Ƃ��A�@
�@�̂Ƃ��A�@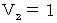 �@�ł��B
�@�ł��B
��W�́@�@�C�v�V���^�C���̂S��������Ԃ̍��W�ϊ�
�@ �� �� �F�@�u ���_���o�R���āA �u�ԓI���x�ύX�����邱�ƂȂ��A ���������^�������Ă��镨�� �v�Ɍ����Č����Ȃ�A ���̕��������݂��鎞��_�́u �C�v�V���^�C���̂S��������ԍ��W�i�@��ԍ��W �C�@���Ύ��� �C �m ��Ύ��� �n�@�j�v����A �������́A ���̕����̈ړ����x��ǂݎ�邱�Ƃ��ł��܂��B ����́A �~���R�t�X�L�[��ԍ��W�ɂ��Ă����l�ł��B �Ȃ��Ȃ�A ���������݂����Q�̎���_���킩��A �����̈ړ����x���킩�邩��ł��B �@���_��ʉ߂��āA ��P�ώ@�Ҍn�ő��� �� �P �œ��������^�������Ă��镨���́A ��P�ώ@�҂ɑ��Ă���Ɣ��Ε����ɑ��� �� �Q �œ��������^�����Ă����Q�ώ@�Ҍn�ւ̍��W�ϊ��̎�
�@���_��ʉ߂��āA ��P�ώ@�Ҍn�ő��� �� �P �œ��������^�������Ă��镨���́A ��P�ώ@�҂ɑ��Ă���Ɣ��Ε����ɑ��� �� �Q �œ��������^�����Ă����Q�ώ@�Ҍn�ւ̍��W�ϊ��̎��@�@
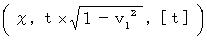 �@�@
�@�@
�@�@�@�@�@�@�@�@�@
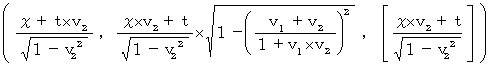
�@�@�@�@�@�@�@�@�@�@�@�� �R�����g �F�@���W�ϊ��ɂāA ���Ύ��Ԃ͕ω����Ă��܂���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
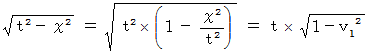
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
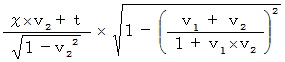
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
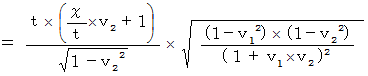
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
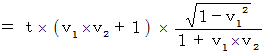
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
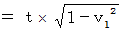
 �@���_��ʉ߂��āA ��P�ώ@�Ҍn�ő��� �� �P �œ��������^�������Ă��镨���́A ��P�ώ@�҂ɑ��Ă���Ɛ��������ɑ��� �|�� �Q �œ��������^�����Ă����Q�ώ@�Ҍn�ւ̍��W�ϊ��̎�
�@���_��ʉ߂��āA ��P�ώ@�Ҍn�ő��� �� �P �œ��������^�������Ă��镨���́A ��P�ώ@�҂ɑ��Ă���Ɛ��������ɑ��� �|�� �Q �œ��������^�����Ă����Q�ώ@�Ҍn�ւ̍��W�ϊ��̎��@�@
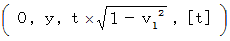 �@�@
�@�@
�@�@�@�@�@�@�@
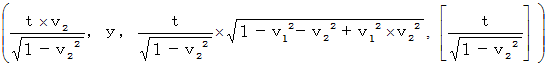
�@�@�@�@�@�@�@�@�@�@�@�@�@�� �R�����g �F�@
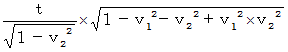
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
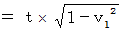
��X�́@�@�Q�̋�_�ɂ����铯�����̑��ΐ�
�@ �}0901 �� �A��P�ώ@�҂̍��W�n�ł��B�@ �}0901
�@�@�@
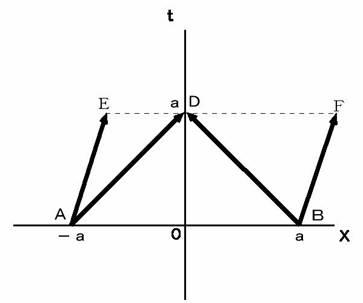
�@�@�@�@�@�@�@�@�@�`�c�F �����`����ώ@�҂ɓ͂����@�@�@�a�c�F �����a����ώ@�҂ɓ͂���
�@�@�@�@�@�@�@�@�@�`�d�F �����`�̉^���@�@�@�@�@�@�@�@�@�@�@�a�e�F �����a�̉^��
�@�@�@�@�@�@�@�@�@�n�c�F ��P�ώ@�҂̉^��
�@ �}0902 �́A �}0901 ���P�ώ@�҂ɑ��đ��� �� �ňړ����Ă����Q�ώ@�҂������Ƃ��̐}�ł��B
�`�f,�@�a�f,�@�c�f�@�́A�t���[�����c�ϊ��𗘗p���ċ��߂܂����B
�@ �}0902
�@�@�@
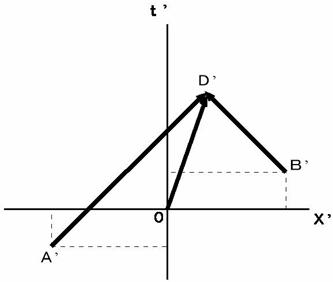
�@�@�@�@�@�@
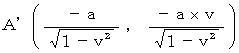 �@�@�@�@�`�f�c�f �F�@���̋O��
�@�@�@�@�`�f�c�f �F�@���̋O���@�@�@�@�@�@
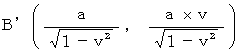 �@�@�@�@�a�f�c�f �F�@���̋O��
�@�@�@�@�a�f�c�f �F�@���̋O���@�@�@�@�@�@
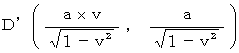 �@�@�@�@�n �c�f �F�@��P�ώ@�҂̋O��
�@�@�@�@�n �c�f �F�@��P�ώ@�҂̋O���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���@�Q�̌����̉^���͏ȗ����܂����B
�@ ���̐}���猾���邱�Ƃ́A ��Q�ώ@�Ҍn�ł́A ��P�ώ@�҂�����_ �c�f �ɒB�������ɂQ�̌�����������ꂽ���������ɑ�P�ώ@�҂ɓ͂��̂��ώ@���܂����A ���ۂɂQ�̌���������������͈قȂ��Ă���Ƃ������Ƃł��B
�@ �ȏ�̂悤�ɁA ���W�ϊ��ɂ���āA �Q�̋�_�̓������������ł��܂��B �������A���̐������@�͒���Ƃ͏����قȂ�܂��B ����́A ��Q�ώ@�҂����P�ώ@�҂ւ̍��W�ϊ��ł��B �ړ����Ă���������������������Q�ώ@�҂ɏՓ˂���ꍇ �� ���������Ɠ������x�ňړ����Ă����P�ώ@�҂ɏՓ˂���ꍇ �Ƃ��r���Ȃ���l�@���܂��B
�@ ����ł́A �����Ԃ̐^�ŐÎ~���Ă��鏗�� �� �v���b�g�z�[���ŐÎ~���Ă���j�� ���o�ꂵ�܂��B �ł͂��ꂩ��A�u �������ǂ�ȑ��x�ňړ����Ă��Ă��A ���ꂩ����������̑����͏�� �P �ł���B�v�Ƃ������ƁA �܂��A�u �ώ@�҂��瓯�������������ꂽ��_�̏��́A �������ɔF�������B�v�Ƃ������Ƃ�O���ɒu���čl���Ă��������B
�@ ����ŁA �v���b�g�z�[���̒j���i ��Q�ώ@�� �j�́A ���̂悤�Ɍ����܂��B
�u �����ɂƂ��ẮA �������瓯�������������ꂽ��Ԃ̍őO���̌����Ɨ�Ԃ̍Ō㕔�̌�����������ꂽ�M�����A �������ɓ�������̂ŁA �Q�̌����͓����Ɍ��������ƂɂȂ�B �������A �ޏ��͂Q�̑M�����Ɍ��Ȃ��̂ŁA �ޏ��ɂƂ��Ă͂Q�̑M���͕ʁX�̎����Ɍ��������ƂɂȂ�B ���̗��R�͎��̂悤�Ȃ��̂ł���B
 �@�@���̊����n�ł́A ��Ԃ̍őO���̌��� �� ��Ԃ̍Ō㕔�̌��� ����A �Q�̑M�����������ɕ������B �������Q�̑M���͓����Ɏ��ɏՓ˂���B
�@�@���̊����n�ł́A ��Ԃ̍őO���̌��� �� ��Ԃ̍Ō㕔�̌��� ����A �Q�̑M�����������ɕ������B �������Q�̑M���͓����Ɏ��ɏՓ˂���B �@�@���̊����n�ł́A ��Ԃ̍őO���̌�������������M���������ꂽ��_ �� ���̑M�����ޏ��ɏՓ˂�����_ �Ƃ̋�Ԃ́A ��Ԃ̍Ō㕔�̌�������������M���������ꂽ��_ �� ���̑M�����ޏ��ɏՓ˂�����_ �Ƃ̋�Ԃ����A �Z���B
�@�@���̊����n�ł́A ��Ԃ̍őO���̌�������������M���������ꂽ��_ �� ���̑M�����ޏ��ɏՓ˂�����_ �Ƃ̋�Ԃ́A ��Ԃ̍Ō㕔�̌�������������M���������ꂽ��_ �� ���̑M�����ޏ��ɏՓ˂�����_ �Ƃ̋�Ԃ����A �Z���B �@�@
�@�@ ��
��  ���A ���̊����n�ł́A �ޏ��͂Q�̑M���Ƃ͕ʁX�̎����ɏՓ˂���B�i �ޏ��͂Q�̑M�����قȂ鎞���Ɋώ@����B�j
���A ���̊����n�ł́A �ޏ��͂Q�̑M���Ƃ͕ʁX�̎����ɏՓ˂���B�i �ޏ��͂Q�̑M�����قȂ鎞���Ɋώ@����B�j �@�@���������āA �ޏ��̊����n�ł��A �ޏ��͂Q�̑M���Ƃ͕ʁX�̎����ɏՓ˂���B�i �ޏ��͂Q�̑M�����قȂ鎞���Ɋώ@����B�j
�@�@���������āA �ޏ��̊����n�ł��A �ޏ��͂Q�̑M���Ƃ͕ʁX�̎����ɏՓ˂���B�i �ޏ��͂Q�̑M�����قȂ鎞���Ɋώ@����B�j �@�@����A ���̊����n�ł��ޏ��̊����n�ł��A ��Ԃ̍őO���̌������ʒu�����_ �� �ޏ����ʒu�����_ �Ƃ̋�Ԃ́A ��Ԃ̍Ō㕔�̌������ʒu�����_ �� �ޏ����ʒu�����_ �Ƃ̋�ԂƁA ��ɒ������������B
�@�@����A ���̊����n�ł��ޏ��̊����n�ł��A ��Ԃ̍őO���̌������ʒu�����_ �� �ޏ����ʒu�����_ �Ƃ̋�Ԃ́A ��Ԃ̍Ō㕔�̌������ʒu�����_ �� �ޏ����ʒu�����_ �Ƃ̋�ԂƁA ��ɒ������������B �@�@�ޏ��̊����n�ł́A �M���������ꂽ��_ �� �������ʒu�����_�́A ����̋�_�ł���B
�@�@�ޏ��̊����n�ł́A �M���������ꂽ��_ �� �������ʒu�����_�́A ����̋�_�ł���B �@�@���������āA �ޏ��̊����n�ł́A ��Ԃ̍őO���̌�������������M���������ꂽ��_ �� ���̑M�����ޏ��ɏՓ˂�����_ �Ƃ̋�Ԃ́A��Ԃ̍Ō㕔�̌�������������M���������ꂽ��_ �� ���̑M�����ޏ��ɏՓ˂�����_ �Ƃ̋�ԂƁA �������������B
�@�@���������āA �ޏ��̊����n�ł́A ��Ԃ̍őO���̌�������������M���������ꂽ��_ �� ���̑M�����ޏ��ɏՓ˂�����_ �Ƃ̋�Ԃ́A��Ԃ̍Ō㕔�̌�������������M���������ꂽ��_ �� ���̑M�����ޏ��ɏՓ˂�����_ �Ƃ̋�ԂƁA �������������B �@�@
�@�@ ��
��  ���A �ޏ��̊����n�ł́A ��Ԃ̍őO���̌��� �� ��Ԃ̍Ō㕔�̌��� ����A �Q�̑M�����قȂ鎞���ɕ�����A �ޏ��͂Q�̑M�����قȂ鎞���Ɋώ@����B�@�@�@�@�v
���A �ޏ��̊����n�ł́A ��Ԃ̍őO���̌��� �� ��Ԃ̍Ō㕔�̌��� ����A �Q�̑M�����قȂ鎞���ɕ�����A �ޏ��͂Q�̑M�����قȂ鎞���Ɋώ@����B�@�@�@�@�v�@ ���̒�����Ԉ���Ă��邱�Ƃɂ��ẮA ��12�́u ��R�ғI�ώ@�̕��� �� �V�������W�ϊ��v�ŏq�ׂ邱�Ƃɂ��܂��B ���āA ����͕ʂɂ��āA �����ŁA�u �Q�̋�_�ɂ����铯�����̑��ΐ� �v�ɂ��āA �R�̂��ƂɌ��y���Ă��������Ǝv���܂��B
�@ �P�Ԗڂ́A ���̒���̒��Ɂu �����s�ς̌��� �v�����ł���؋����܂܂�Ă���悤�Ɏv���邱�Ƃ������Ƃ������Ƃł��B ���̌�����l���͎��̂悤�Ȃ��̂ł��B
�u �v���b�g�z�[���̒j�����炷��ƁA ��Ԃ̍őO����������ꂽ������Ԃ̒��̏����ɓ͂��̂ɂ����鎞�Ԃ́A ��Ԃ̒����̔����̋����̒l�������Ȃ����Ԃł���B�i �ځE�H�E�c �P�ʌn ��O��ɂ��Ă��܂��B�j�@���̏ꍇ�A �w ���́A ��Ԃ̒��̐l���炷��ƁA ��Ԃ̒����̔����̋��� �� ��Ԃ̒����̔����̋����̒l�������Ȃ����� �œ`���B�x ���������āA ��Ԃ̒��̐l�ɑ�����̑��ΓI�ȑ����� �P �ȏ�ɂȂ�B ����āA �w �����s�ς̌��� �x �͌��ł���B�v
�@ ���̊��Ⴂ�́A ���ΐ����_�𗝉����邽�߂ɑ�ςɏd�v�ȃ|�C���g�ł��B �m���ɁA�v���b�g�z�[���̐l���炷��ƁA �������������ł��B�u �����ƈړ������ԂƂ̃R���{���[�V�������������z����B ����āA ��Ԃ̒��̐l�ɑ�����̑��ΓI�ȑ����� �P �ȏ�ł���B�v�ƌ��������Ȃ�܂��B �������A ���ۂɁA ��Ԃ̒��̐l�̗���ɗ����čl���Ă݂Ă��������B ����ƁA ����ς���̑����� �P �ł��邱�Ƃ��킩��܂��B ���������ΐ����_�̑�햡�Ȃ̂ł��B
�@ ���̂悤�Ɋ��Ⴂ���������́A ���̂悤�ȗ��R�ł��B
�u�@�w �v���b�g�z�[���̐l���炷��ƁA ���́A ����
 �ŁA ��Ԃ̒����̔����̋����̒l�������Ȃ��������A ��Ԃ̒����̔����̋����̒l�������Ȃ����ԂŁA ��Ԃ̒��̐l�ɓ`���B�x ����Ƃ����āA �w ��Ԃ̒��̐l���炷��ƁA ���́A ��Ԃ̒����̔����̋��� �� ��Ԃ̒����̔����̋����̒l�������Ȃ����ԂŁA �����ɓ`���B�x �Ƃ͌����Ȃ��̂ł��B �Ȃ��Ȃ�A ��҂̕��͂ł́A �w ��Ԃ̒��̐l���炷��ƁA �x �ƌ����Ă����Ȃ���A �����`��鎞�Ԃ��v���b�g�z�[���̐l�̍��W�n�ɑ����Ă��邩��ł��B
�ŁA ��Ԃ̒����̔����̋����̒l�������Ȃ��������A ��Ԃ̒����̔����̋����̒l�������Ȃ����ԂŁA ��Ԃ̒��̐l�ɓ`���B�x ����Ƃ����āA �w ��Ԃ̒��̐l���炷��ƁA ���́A ��Ԃ̒����̔����̋��� �� ��Ԃ̒����̔����̋����̒l�������Ȃ����ԂŁA �����ɓ`���B�x �Ƃ͌����Ȃ��̂ł��B �Ȃ��Ȃ�A ��҂̕��͂ł́A �w ��Ԃ̒��̐l���炷��ƁA �x �ƌ����Ă����Ȃ���A �����`��鎞�Ԃ��v���b�g�z�[���̐l�̍��W�n�ɑ����Ă��邩��ł��B�@ ��Ԃ̒��̐l�ɂƂ��Ă��A ���̑�����
 �ł��̂ŁA �����`��鎞�ԂƋ����͓������Ȃ��Ă͂Ȃ�܂���B ��Ԃ̒��̐l�̍��W�n�̎��ԂƋ�Ԃ�p��������Ȃ�͂��ł��B ��Ԃ����Ԃ���Ԃ̒��̐l�̍��W�n�̂��̂��g�p���Ȃ�����A ��Ԃ̒��̐l�̊ώ@���e�͐��m�ɂ͂킩��Ȃ��̂ł��B�@�v
�ł��̂ŁA �����`��鎞�ԂƋ����͓������Ȃ��Ă͂Ȃ�܂���B ��Ԃ̒��̐l�̍��W�n�̎��ԂƋ�Ԃ�p��������Ȃ�͂��ł��B ��Ԃ����Ԃ���Ԃ̒��̐l�̍��W�n�̂��̂��g�p���Ȃ�����A ��Ԃ̒��̐l�̊ώ@���e�͐��m�ɂ͂킩��Ȃ��̂ł��B�@�v�@ ���x�̍��W�ϊ��i ���x�̍��� �j�ɂ����āA �K�����C�ϊ��ɂ��u ��R�ғI�ȑ��ΓI�ȑ��� �v�́@���f�@���@�� �P �{ �� �Q�@�ł���A ���[�����c�ϊ��ɂ��u �����҂ɂƂ��Ă̑��� �v�́@
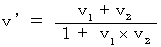 �@�ł��B ���ΐ����_�́A�u ��R�ғI�Ȋώ@�ł͖{���̂Ƃ���̐��m�Ȋώ@�͕s�\�ł���̂ŁA ��ɓ����҂̗���ɗ����čl���Ȃ���Ȃ�Ȃ��B�v�ƁA �������Ɍ�肩���Ă���܂��B
�@�ł��B ���ΐ����_�́A�u ��R�ғI�Ȋώ@�ł͖{���̂Ƃ���̐��m�Ȋώ@�͕s�\�ł���̂ŁA ��ɓ����҂̗���ɗ����čl���Ȃ���Ȃ�Ȃ��B�v�ƁA �������Ɍ�肩���Ă���܂��B�@ �Ƃ���ŁA �������̂悤�ł���Β��낪�����̂ł����A �c�O�Ȃ���A ����ł́u �����s�ς̌��� �v�����藧���Ă��܂���B
�@�@�@��Q�ώ@�҂ɂƂ��ẮA��Q�ώ@�҂ɓ͂���Ԃ̍őO����������ꂽ���̑��� �F�@

�@�@�@��Q�ώ@�҂ɂƂ��ẮA��P�ώ@�҂ɓ͂���Ԃ̍őO����������ꂽ���̑��� �F�@
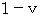
�@�@�@��Q�ώ@�҂ɂƂ��ẮA��Q�ώ@�҂ɓ͂���Ԃ̍Ō㕔��������ꂽ���̑��� �F�@

�@�@�@��Q�ώ@�҂ɂƂ��ẮA��P�ώ@�҂ɓ͂���Ԃ̍Ō㕔��������ꂽ���̑��� �F�@
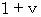
�@ �����̑����ɊW�Ȃ��A �ǂ�Ȋ����n�ł����̓`��鑬����
 �ł��B �Ƃ������Ƃ́A �����ɑ��Ă��܂��܂ȑ��x�ňړ����Ă��邷�ׂĂ̊ώ@�҂́A �����̍��W�n�ł́i �����̍��W�n�ł́A �����͐Î~���Ă��܂� �j�A ���������Ă���A ���̎��_�ł̌����Ɗώ@�҂Ƃ̋�ԋ����̒l�ɓ��������Ԍ�ɁA ���̌�������Ƃ������Ƃł��B �ł�����A �����ώ@�҂����������������ꂽ��_��������ꂽ�Q�̌����Ɍ����̂ł���A �Q�̌��͓����Ɍ��������ƂɂȂ�̂ł��B �������A ��Q�ώ@�҂��A ��R�ғI���A �ړ����Ă����P�ώ@�҂����������Ƃ�����ώ@����ꍇ���l�������ɂ́A �����͂Ȃ�Ȃ��̂ł��B
�ł��B �Ƃ������Ƃ́A �����ɑ��Ă��܂��܂ȑ��x�ňړ����Ă��邷�ׂĂ̊ώ@�҂́A �����̍��W�n�ł́i �����̍��W�n�ł́A �����͐Î~���Ă��܂� �j�A ���������Ă���A ���̎��_�ł̌����Ɗώ@�҂Ƃ̋�ԋ����̒l�ɓ��������Ԍ�ɁA ���̌�������Ƃ������Ƃł��B �ł�����A �����ώ@�҂����������������ꂽ��_��������ꂽ�Q�̌����Ɍ����̂ł���A �Q�̌��͓����Ɍ��������ƂɂȂ�̂ł��B �������A ��Q�ώ@�҂��A ��R�ғI���A �ړ����Ă����P�ώ@�҂����������Ƃ�����ώ@����ꍇ���l�������ɂ́A �����͂Ȃ�Ȃ��̂ł��B�@ �Q�Ԗڂ́A �ώ@�҂��u ������ �v��F�����邩�ǂ�������ɂ��Ă���̂ł͂Ȃ��Ƃ������Ƃł��B
�@ �܂��A ����̂Ȃ��悤�A�u ������ �v�Ƃ́A�u ����Q�̎��ۂ��������鎞�������������Ƃł���B�v�Ƃ������Ƃ��m�F���Ă��������Ǝv���܂��B ������ԈႦ�āA�u �ώ@�҂��Q�̎��ۂ��ɔF�����邱�� �v�ƕ߂��Ă͂����܂���B ����ƁA�u �ώ@�҂�����܂����Ɣ�ώ@�҂�����܂������A �ώ@�҂ɂƂ��ē������ɂȂ邽�߂ɂ́A �����A �Q�l�̋�����
 ����Ă���Ȃ�A ��ώ@�҂�
����Ă���Ȃ�A ��ώ@�҂�  �̎��ԑ����܂�������������B�v�Ƃ���������l���������Ă��܂����ƂɂȂ�܂��B ���ۂɂ́A �Q�l�������ɏu�����������́A ���݂��ɑ���̕����x��Ă܂����������悤�ɔF������̂ł��B ���ΐ����_�́A�u ��ǂ̂悤�Ɋώ@�҂ɓ`���A ���ꂪ�ώ@�҂���ǂ̂悤�ɔF�������̂��H�v�Ƃ������ƂɊւ��ẮA ���y���Ă��܂���B �Ȃ��Ȃ�A ���ΐ����_�́A �ώ@�҂̔F�m��Njy����u �F���_ �v�̗��_�ł͂Ȃ��āA �ώ@�҂̎�ϓI�Ȏ���Ԃɂ����镨���̋q�ϓI�ȉ^�������߂�u �����w �v�̗��_������ł��B
�̎��ԑ����܂�������������B�v�Ƃ���������l���������Ă��܂����ƂɂȂ�܂��B ���ۂɂ́A �Q�l�������ɏu�����������́A ���݂��ɑ���̕����x��Ă܂����������悤�ɔF������̂ł��B ���ΐ����_�́A�u ��ǂ̂悤�Ɋώ@�҂ɓ`���A ���ꂪ�ώ@�҂���ǂ̂悤�ɔF�������̂��H�v�Ƃ������ƂɊւ��ẮA ���y���Ă��܂���B �Ȃ��Ȃ�A ���ΐ����_�́A �ώ@�҂̔F�m��Njy����u �F���_ �v�̗��_�ł͂Ȃ��āA �ώ@�҂̎�ϓI�Ȏ���Ԃɂ����镨���̋q�ϓI�ȉ^�������߂�u �����w �v�̗��_������ł��B�@ �ł�����A�u �Q�̋�_�̓������̑��ΐ� �v�ɂ��ďؖ����邽�߂ɂ́A ���ԍ��W���������Q�̎���_���A ���W�ϊ��ɂ���āA ���ԍ��W���قȂ�Q�̎���_�ɂȂ��Ă��܂����Ƃ����������̂ł��B ����ɂ́A ���[�����c�ϊ��̎�������������������킯�ł��B ���̐����̒��́A ����ώ@�҂̋O�Ղ͕K�v�Ȃ��̂ł��B
�@ �R�Ԗڂ́A �u �Q�̋�_�̓������̑��ΐ� �v�͌������̌��ۂł����Ƃ������Ƃł��B ���̂��Ƃ�������邽�߂ɁA �����u ���ꂪ�����ꂽ���� �v�Ƃ������������Ă�����̂Ƃ��āA ��P�ώ@�҂����Q�ώ@�҂ւ̍��W�ϊ����l���Ă݂܂��傤�B �܂��A ���̏͂̍ŏ��ɒ����Q�̐}�i �}0901 �� �}0902 �j��������x���Ă��������B ���ꂪ�I���܂�����A �����v�������ׂĂ��������A �c�ɂ̉w�̖�̃v���b�g�z�[�����B ���}��Ԃ��v���b�g�z�[����ʉߒ��ɁA ��Ԃ̑O�ƌ�̗��[�Ɏ��t����ꂽ�Q�̎��v�������Ɍ����āA ���̌����z�[���̒����Ŋe�w��Ԃ̗�Ԃ�҂��Ă���l�i ��P�ώ@�� �j�̎��E�ɓ����ɔ�э���ł��܂��B ���̌��i���A �w�̑������ԂƔ��Ε����ɑ����Ă���Ԃɏ�����l�i ��Q�ώ@�� �j�����Ă��܂��B �Q�̎��v���������̂́A ���傤�� ��Ԃ̒��� �� ��P�ώ@�� �� ��Q�ώ@�� ���d�Ȃ������ł��B �}0901 �̑�P�ώ@�҂ɂƂ��āA �����̎��v��
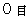 �������Ă���Ƃ���������ɔ�э���ł��܂��B ���̂��Ƃ��ώ@���Ă��� �}0902 �̑�Q�ώ@�҂́A ���̂悤�ɍl���č������Ă����܂��B
�������Ă���Ƃ���������ɔ�э���ł��܂��B ���̂��Ƃ��ώ@���Ă��� �}0902 �̑�Q�ώ@�҂́A ���̂悤�ɍl���č������Ă����܂��B �@�@��P�ώ@�҂������Ă�悤�ɁA �����̎��v��
�@�@��P�ώ@�҂������Ă�悤�ɁA �����̎��v�� 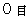 �������Ă���Ƃ������P�ώ@�҂ɓ����ɔ�э���ł��������Ƃ́A �܂��ԈႢ�Ȃ��B ��P�ώ@�҂ɂƂ��Ă͎��v�͗����Ƃ������Ă���̂��B
�������Ă���Ƃ������P�ώ@�҂ɓ����ɔ�э���ł��������Ƃ́A �܂��ԈႢ�Ȃ��B ��P�ώ@�҂ɂƂ��Ă͎��v�͗����Ƃ������Ă���̂��B �@�@�ł��A �}0902�̂悤�ɁA �����炷��ƁA �Q�̎��v�������������́A �ǂ����
�@�@�ł��A �}0902�̂悤�ɁA �����炷��ƁA �Q�̎��v�������������́A �ǂ���� 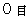 �ł͂Ȃ����A �ʁX�̎����Ɏ��̊�ɔ�э���ł���B ��Ɏ��̊�ɔ�э���ł����Ɍ��������v��
�ł͂Ȃ����A �ʁX�̎����Ɏ��̊�ɔ�э���ł���B ��Ɏ��̊�ɔ�э���ł����Ɍ��������v�� 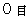 ���������������̂�����i��ł���A ��Ɍ��������v��
���������������̂�����i��ł���A ��Ɍ��������v�� 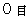 ������Ɍ������̂�����x��Ă���B �������A ���ꂪ���������̏����Ȃ̂��B
������Ɍ������̂�����x��Ă���B �������A ���ꂪ���������̏����Ȃ̂��B �@�@�������҂Ă�I�H ��P�ώ@�҂Ǝ��i��Q�ώ@�ҁj�̊ώ@���e�̈Ⴂ�́A ��Ԃ̑��������ł���B ���́A ��P�ώ@�҂ł�����̂��B �Ƃ������Ƃ́A ���̊ώ@���e�́A �}0901�Ɏ��Ă���A �Q�̌����̑����������Ȃ��Ă��邾���̂��Ƃł͂Ȃ��̂��H
�@�@�������҂Ă�I�H ��P�ώ@�҂Ǝ��i��Q�ώ@�ҁj�̊ώ@���e�̈Ⴂ�́A ��Ԃ̑��������ł���B ���́A ��P�ώ@�҂ł�����̂��B �Ƃ������Ƃ́A ���̊ώ@���e�́A �}0901�Ɏ��Ă���A �Q�̌����̑����������Ȃ��Ă��邾���̂��Ƃł͂Ȃ��̂��H �@�@�������A ���ɂƂ��Ĉړ����Ă����P�ώ@�҂��A ��P�ώ@�҂ɂƂ��Ă͈ړ����Ă��Ȃ��̂ł��邩��A ���Ƒ�P�ώ@�҂̗����Ƃ����ړ����Ă��Ȃ��}���d�˂Ă݂悤�B ����ƁA ���̂Ƃ���Ԃ̑����͈قȂ邯��ǂ��A �Q�̎��v�͂Q�l�ɂƂ��ē����Ɍ���A �������A ���̓`��鑬���́A �����̑��x�ɂ͖��W�łǂ�Ȋ����n�ł����Ȃ̂�����A �Q�l�ɂƂ��āA �������i
�@�@�������A ���ɂƂ��Ĉړ����Ă����P�ώ@�҂��A ��P�ώ@�҂ɂƂ��Ă͈ړ����Ă��Ȃ��̂ł��邩��A ���Ƒ�P�ώ@�҂̗����Ƃ����ړ����Ă��Ȃ��}���d�˂Ă݂悤�B ����ƁA ���̂Ƃ���Ԃ̑����͈قȂ邯��ǂ��A �Q�̎��v�͂Q�l�ɂƂ��ē����Ɍ���A �������A ���̓`��鑬���́A �����̑��x�ɂ͖��W�łǂ�Ȋ����n�ł����Ȃ̂�����A �Q�l�ɂƂ��āA �������i �j�Ɂu���v��
�j�Ɂu���v�� 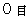 �̎����Ɍ���܂�����B�v�Ƃ������m�ȏ����������Q�̌����Q�l�̊�ɔ�э���ł���̂ł͂Ȃ��낤���H
�̎����Ɍ���܂�����B�v�Ƃ������m�ȏ����������Q�̌����Q�l�̊�ɔ�э���ł���̂ł͂Ȃ��낤���H �@�@�����A ��Ԃ̑����� �O �ł������Ȃ�A ���̂Ƃ��́A ���͑�P�ώ@�҂ɂȂ�A ��Q�ώ@�҂͑�P�ώ@�҂ɂȂ�B
�@�@�����A ��Ԃ̑����� �O �ł������Ȃ�A ���̂Ƃ��́A ���͑�P�ώ@�҂ɂȂ�A ��Q�ώ@�҂͑�P�ώ@�҂ɂȂ�B �@�@���������u�����ꂽ���̒��̂�������Ɉړ�������q�ɂ��Ă����A ����́A ��O�ώ@�ҁA ��P�ώ@�ҁA ��Q�ώ@�ҁA ���ꂼ��ɂƂ��ĈقȂ���̂ɂȂ��Ă���̂ł͂Ȃ��낤���H�@�܂�A ���ꂼ��̊ώ@�҂̊����n�̐��������q������̂ł͂Ȃ��̂��H
�@�@���������u�����ꂽ���̒��̂�������Ɉړ�������q�ɂ��Ă����A ����́A ��O�ώ@�ҁA ��P�ώ@�ҁA ��Q�ώ@�ҁA ���ꂼ��ɂƂ��ĈقȂ���̂ɂȂ��Ă���̂ł͂Ȃ��낤���H�@�܂�A ���ꂼ��̊ώ@�҂̊����n�̐��������q������̂ł͂Ȃ��̂��H �@�@�Ƃ������Ƃ́A �{���́A �Q�l�Ƃ��������ɁA �Q�̎��v���������Ɍ��������Ƃ�m��̂����A ����̂��Ƃɂ��ẮA ���̂悤�ɂȂ��Ă��邱�Ƃ��A ���݂��ɂ킩��Ȃ��Ƃ����̂��^���Ȃ̂ł͂Ȃ����낤���H
�@�@�Ƃ������Ƃ́A �{���́A �Q�l�Ƃ��������ɁA �Q�̎��v���������Ɍ��������Ƃ�m��̂����A ����̂��Ƃɂ��ẮA ���̂悤�ɂȂ��Ă��邱�Ƃ��A ���݂��ɂ킩��Ȃ��Ƃ����̂��^���Ȃ̂ł͂Ȃ����낤���H�@�@�@�@�@�@�@���@�u ���v�������Ă��� �v�Ƃ����Ƃ��ɂ́A���̂Q�̈Ӗ�������܂��B
�@�@�@�@�@�@�@�@�P�Ԗڂ́A�u ���̎��v�͂T���i��ł���B�v�Ƃ��u �P�O���x��Ă���B�v
�@�@�@�@�@�@�@�@�Ƃ����Ӗ��ł��B �Q�Ԗڂ́A�u ���̎��v�͓d�r���ꂩ���Ă��āA ��
�@�@�@�@�@�@�@�@������Ɠ����Ă���B�v�Ƃ��A�u �P���ԂɂV�O���Ԃ�����ł��܂��B�v�Ƃ�
�@�@�@�@�@�@�@�@���Ӗ��ł��B
�@�@�@�@�@�@�@�@�@���ΐ����_�ł́A ���v���������Ƃ͂���܂���B�u �Q�̋�_�ɂ�
�@�@�@�@�@�@�@�@���铯�����̑��ΐ� �v��u ���̌o�߃X�s�[�h�̑��ΐ� �v�́A ���v
�@�@�@�@�@�@�@�@�̋����������Ă���̂ł͂���܂���B
��P�O�́@�@�S��������Ԃ̍��W�ϊ��̗�
�@ �X�P�b�`���₷�����邽�߂ɁA �S��������Ԃ��A ��Ԃ��Q�����Ƃ���R��������Ԃł���Ɖ��z���Ă��������B�i�P�j��P�ώ@�҂̍��W�n
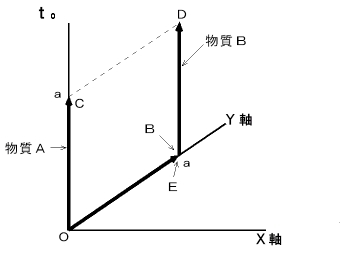
�i ���P �j�@�Q�̕������Î~���Ă���A ���鎞���ɕ����`�������������܂����B ���������ꂽ����_�����_�Ƃ��āA ���̌��������a�ɓ͂��܂ł̏��C�v�V���^�C���̎���ԍ��W�ŁA �}1001 �ɕ\���Ă��������B �������A �Q�̕����͂x����ɂ�����̂Ƃ��Ă��������B
�i �� �j
�@�}1001
�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
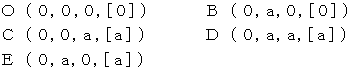
�@�@�@�@�@�@�@���@����_�̍��W�͎��̂悤�ɕ\����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@
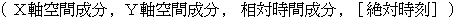
�i�Q�j��Q�ώ@�҂̍��W�n
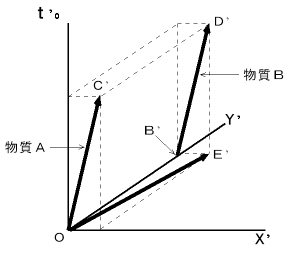
�i ���Q �j�@��L�̏��A ��P�ώ@�҂ɑ��Ăw���̕��̕����ɑ���
 �œ��������^�������Ă���l���ώ@�������A ���������ꂽ����_�����_�Ƃ��āA �}1002 �ɕ\���Ă��������B
�œ��������^�������Ă���l���ώ@�������A ���������ꂽ����_�����_�Ƃ��āA �}1002 �ɕ\���Ă��������B�i �� �j
�@�}1002
�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
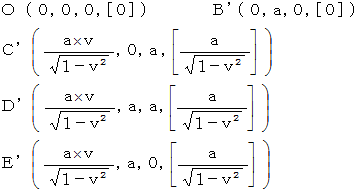
�@�@�@�@�@�@�@�@�@�@�@���@
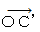 �̑傫�����@
�̑傫�����@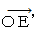 �̑傫�����A ���Ɂ@
�̑傫�����A ���Ɂ@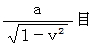 �@�ł��B
�@�ł��B