Chapter 2 True Role of Proper time
True Role of Proper time
Relative time, i.e. proper time, is not content with relative, illusive, and dimensional time. It has the important role which determines 'frequency of ligh' , 'mass' , 'perpendicular speed', and 'Coulomb force.'Please return to Figure 0101 again. What should we do to find the difference of relative-time intervals of two balls? It is easy. We only have to fly clocks instead of balls. Please imagine weightless and vaccum universe. Now, two clocks are traveling with linear uniform motion in the same direction at different speed. The clock
 is faster than the clock
is faster than the clock  , and the distance between two clocks is getting shorter. You are traveling with the same velocity as the clock
, and the distance between two clocks is getting shorter. You are traveling with the same velocity as the clock  on a straight line; this line is slightly nearer a straight line of orbit of the clock
on a straight line; this line is slightly nearer a straight line of orbit of the clock  than the middle of two parallel straight lines of obits of two flying clocks. You and the clock
than the middle of two parallel straight lines of obits of two flying clocks. You and the clock  are going to be overtaken by the clock
are going to be overtaken by the clock  soon. Your observation starts from this situation. Please see Figure 0201.
soon. Your observation starts from this situation. Please see Figure 0201.Figure 0201
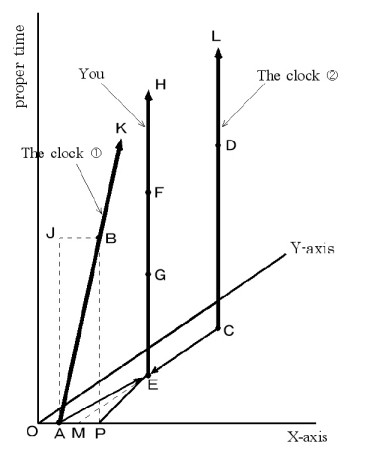
First, when the clock
 is on the space-time point
is on the space-time point  , please record times of the clock
, please record times of the clock  and the clock
and the clock  simultaneously. Second, when the clock
simultaneously. Second, when the clock  is on the space-time point
is on the space-time point  , please record times of two clocks simultaneously. Last, by comparing the time intervals of two clocks, you find the difference of relative-time intervals of two clocks.
, please record times of two clocks simultaneously. Last, by comparing the time intervals of two clocks, you find the difference of relative-time intervals of two clocks.By the way, please notice the next statement:
 The space-time point on which you record firstly times of two clocks are not the space-time point
The space-time point on which you record firstly times of two clocks are not the space-time point  but the space-time point
but the space-time point 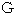 . Because you can see the clock thanks to light coming from the clock. It takes some time intervals that the light reaches you.
. Because you can see the clock thanks to light coming from the clock. It takes some time intervals that the light reaches you.
How is the result of measurement? Oh my god! There is no difference. Why no !? The truth may be one of whether
 There is no difference really.
There is no difference really. or
or  The method of measurement is wrong.
The method of measurement is wrong. As a matter of fact, the method of measurement is wrong. That is, the way of thinking about the method of measurement was right, but it was mistake that we thought relative-time intervals could be measured with a clock.
As a matter of fact, the method of measurement is wrong. That is, the way of thinking about the method of measurement was right, but it was mistake that we thought relative-time intervals could be measured with a clock.Actually, a clock is a tool not for measuring relative-time intervals but for measuring absolute-time intervals.
Then, how can we measure relative-time intervals? To tell the truth, we can measure them with light. We only have to use the property of light as follows:
 A number of vibrations of photon on electromagnetic wave in a light source per unit absolute-time interval, in other words 'frequency of photon on electromagnetic wave', is constant, even if any observer traveling with linear uniform motion observes it. vibrations of photon on electromagnetic wave are decomposed into the relative-time axis component and the space axes components, and then only the relative-time axis component of ovibrations travels through space at the speed of light.
A number of vibrations of photon on electromagnetic wave in a light source per unit absolute-time interval, in other words 'frequency of photon on electromagnetic wave', is constant, even if any observer traveling with linear uniform motion observes it. vibrations of photon on electromagnetic wave are decomposed into the relative-time axis component and the space axes components, and then only the relative-time axis component of ovibrations travels through space at the speed of light.
If it is under no influence of 'Doppler effect', a frequency of traveling light is equal to that of the relative-time axis component of optical vibrations of a photon in a light source. The property of light is expressed in Figure 0202.
Figure 0202
Optical vibrations of a photon in a light source are decomposed into the relative-time axis component and the space axes components as a result of a movement of a light source which is the container of a photon. And then, only the relative-time axis component of optical vibrations travels at the speed of light. Therefore, the faster a speed of a light source, the smaller a frequency of traveling light. Because, the longer
 space intervals through which an object travels per unit absolute-time interval
space intervals through which an object travels per unit absolute-time interval , the shorter
, the shorter  relative-time intervals through which the object travels per unit absolute-time interval.
relative-time intervals through which the object travels per unit absolute-time interval.
Now, let us consider that light sources are traveling instead of clocks. Please see Figure 0201 again. We consider that two light sources emit lights of the same frequency on the condition that they keep still. A frequency of light emitted from a traveling light source is less than that emitted from a stationary light source as the ratio of relative-time intervals to absolute-time intervals. Because, optical vibrations of a photon are decomposed into the relative-time axis component and space axes components, and then only the relative-time axis component of optical vibrations travels. Therefore, a wavelength of light emitted from a traveling light source is longer than that emitted from a stationary light source, because the speed of light is constant.
 [ wavelength ]
[ wavelength ]  [ wave speed ]
[ wave speed ]The experiment has proved this phenomenon. It is called 'Transverse Doppler effect.' I think, however, that this phenomenon is not due to 'Doppler effect.' Therefore, I call it 'extension of a wavelength according to the law of optical vibrations of a photon.'
We have understood the role of relative-time, i.e. proper time, a little. We must get it more deeply. We return to Figure 0101 once again. First, please notice the difference in the masses of two balls
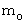 and
and 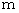 . Next, please remember that two balls fly spinning at the same speed. Last, please imagine that two kindergarteners are measuring an amount of the water in their own bucket. They are scooping up water in a bucket with each glass. The glass of Yuki has a twice much capacity as that of Mai. As a result of their measurement, water in Yuki's bucket is three cups of glass, and water in Mai's bucket is six cups of glass. So, Yuki says :
. Next, please remember that two balls fly spinning at the same speed. Last, please imagine that two kindergarteners are measuring an amount of the water in their own bucket. They are scooping up water in a bucket with each glass. The glass of Yuki has a twice much capacity as that of Mai. As a result of their measurement, water in Yuki's bucket is three cups of glass, and water in Mai's bucket is six cups of glass. So, Yuki says :  The amount of water in my backet is the half of Mai's .
The amount of water in my backet is the half of Mai's . Mai says :
Mai says :  I think you'er right.
I think you'er right. Is it a lovely talk, isn't it ? It is clear that the amounts of water in their buckets are equal. To tell the truth, Nature supports such misunderstanding in special case. It is the case that the following replacements are done:
Is it a lovely talk, isn't it ? It is clear that the amounts of water in their buckets are equal. To tell the truth, Nature supports such misunderstanding in special case. It is the case that the following replacements are done: An amount of water in a bucket
An amount of water in a bucket

 A capacity of a glass
A capacity of a glass

 A measured number of cups
A measured number of cups

In this case, please consider that Yuki keeps still and Mai is traveling. Therefore, on one hand, for Yuki, relative-time intervals which Yuki travels per certain absolute-time intervals are equal to those absolute-time intervals. On the other hand, for Yuki, relative-time intervals which Mai travels per those absolute-time intervals are shorter than those absolute-time intervals. For Yuki, the glass of Mai is not as large as Mai thinks. For example, for Yuki,
 a number of spins of an object per unit relative-time interval measured by Mai who has relative-time intervals of half length of Yuki
a number of spins of an object per unit relative-time interval measured by Mai who has relative-time intervals of half length of Yuki is twice as much as that measured by Yuki. The reason is that
is twice as much as that measured by Yuki. The reason is that a number of spins of an object per certain absolute-time intervals
a number of spins of an object per certain absolute-time intervals is constant for two kindergarteners.
is constant for two kindergarteners.Please reqard
 a measured number of spins of an object per unit relative-time interval
a measured number of spins of an object per unit relative-time interval as
as  the measured mass of the object.
the measured mass of the object. Actually mass shows total energy of an object. Therefore, as a speed of an object increases, mass of the object increases, because kinetic energy is added. an object may travel or may not travel according to the way of observation. That is, a movement of an object changes due to a relationship on movement between an observer and an observed object. Therefore, mass of an object changes due to a relationship on movement between an observer and the observed object.
Actually mass shows total energy of an object. Therefore, as a speed of an object increases, mass of the object increases, because kinetic energy is added. an object may travel or may not travel according to the way of observation. That is, a movement of an object changes due to a relationship on movement between an observer and an observed object. Therefore, mass of an object changes due to a relationship on movement between an observer and the observed object.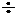 A capacity of a glass
A capacity of a glass A number of cups
A number of cups

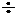 Relative-time intervals
Relative-time intervals Mass of the object
Mass of the object
Chapter 3 Proposal of New System of units
Proposal of New System of units
(1) Proposal of new system of unitsAlthough human beings have made the present system of units out of a human life, we should replace the present system of units with a new system of units to simplify the expression on physics. Therefore, I propose changing the system of units as follows:
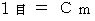
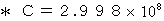
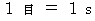
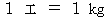
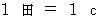
It is the most noticeable feature of the new system of units that the unit of time is the same as the unit of space. The speed of light is
 in the new system of units. I call this new system of units
in the new system of units. I call this new system of units 
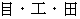 system of units.
system of units. It is pronounced 'mok-ko-den system of units.'
It is pronounced 'mok-ko-den system of units.'We make
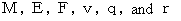 in the
in the 
 system of units correspond to
system of units correspond to 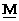 ,
, 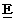 ,
, 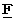 ,
, 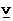 ,
, 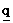 , and
, and  in the
in the 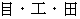 system of units , respectively. Then, it is as follows :
system of units , respectively. Then, it is as follows :
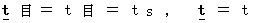
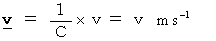
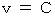 into this equality, we obtain
into this equality, we obtain 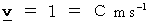 .
. in the new system of units.
in the new system of units.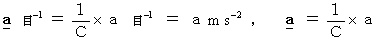
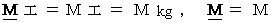

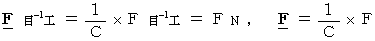
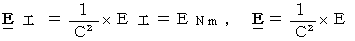
Moreover, we can describe some equations showing mechanical or electro-magnetic or relativistic law as follows :

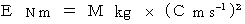 ,
,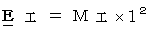
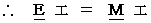
 (Equation 3-1)
(Equation 3-1)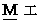 has
has 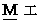 .
.
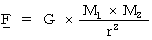 ,
,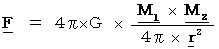

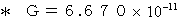
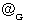 as the constant of (Equality 3-2) :
as the constant of (Equality 3-2) : 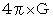 .
.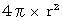

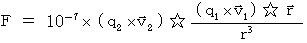 ,
,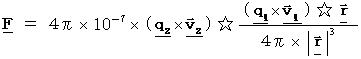

 stands for vector product.
stands for vector product. as the constant of (Equality 3-3) :
as the constant of (Equality 3-3) : 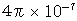 .
.
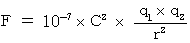
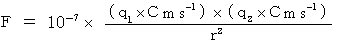
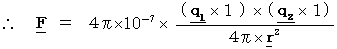

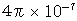 is the same as
is the same as of
of
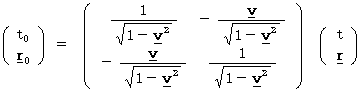
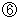
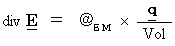
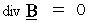
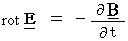
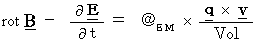
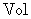 be volume of space occupied by electric
be volume of space occupied by electric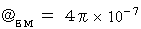
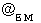
 Electromagnetic transmittance
Electromagnetic transmittance .
.I use

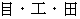 system of units
system of units from now on.
from now on.I use
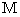 ,
, 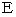 ,
, 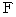 ,
,  , and
, and 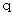
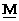 ,
, 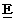 ,
, 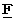 ,
, 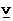 , and
, and 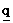 , respectively.
, respectively.(2) Units of quantity in
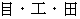 system of units
system of units1. Proposal of name of base quantities

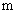 or
or 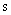 )
)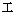
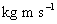 )
)  (
( 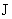 )
)  (
( 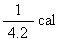 )
) (
( 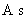 )
) 'Space-time point' is a linear number. 'Space-time intervals' is
'Space-time point' is a linear number. 'Space-time intervals' is ( ) shows SI units.
( ) shows SI units. Temperature (
Temperature (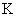 ), Luminous intensity (
), Luminous intensity (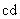 ), and Amount of
), and Amount of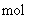 ) are base quantities, too.
) are base quantities, too. 'Base units' is shown with combination of units of base quantities.
'Base units' is shown with combination of units of base quantities.2. Quantity :
 .
.
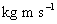 )
)3. Quantity :
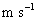 )
)4. Quantity :
 .
.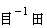
 )
)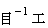
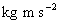 )
)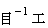
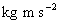 )
)  (
( 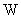 )
)5. Quantity :
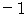 .
.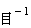
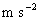 )
)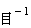
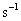 )
)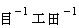
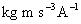 )
)6. Basic units of Constant

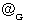
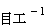


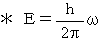
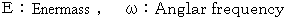
7. '
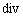 ' and '
' and '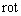 ' make basic units change.
' make basic units change.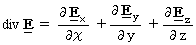
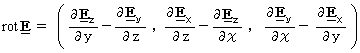
The '
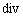 ' is an operator, i.e. function, which obtains a scalar from a vector. Obtained scalar shows amount of vector welling up in minimum space. When we make the operator '
' is an operator, i.e. function, which obtains a scalar from a vector. Obtained scalar shows amount of vector welling up in minimum space. When we make the operator ' ' exert an influence on electromagnetic field, its basic unit changes from
' exert an influence on electromagnetic field, its basic unit changes from  to
to 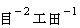 .
.The '
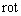 ' is an operator which changes a vector to different vector. Obtained vector shows moment of force to turn a bear by current of total vectors in minimum space. When we make the operator '
' is an operator which changes a vector to different vector. Obtained vector shows moment of force to turn a bear by current of total vectors in minimum space. When we make the operator '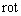 ' exert an influence on electromagnetic field, its basic unit changes from
' exert an influence on electromagnetic field, its basic unit changes from 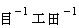 to
to 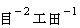 .
.
Chapter 4 Lorentz Transformation
Lorentz Transformation
The source of the special theory of relativity is 'Lorentz transformation' which comes from the axiom:  The speed of light is constant in all inertial frames of reference.
The speed of light is constant in all inertial frames of reference.
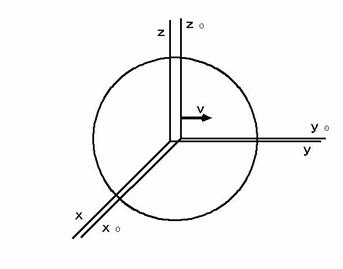
Please see Figure 0401. There are two coordinate systems. One of them is the stationary coordinate system with x y z - coordinates , and the other is the traveling coordinate system with xo yo zo - coordinates; the xo yo zo - coordinate system is traveling in the positive direction of the Y-axis of the x y z - coordinate system. Let us think how the light, which is emitted for a instant on the coordinate origin at the very moment two coordinates are piled up, travels throgh space in each coordinate system.
Let
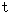 be time of x y z - coordinate system.
be time of x y z - coordinate system.Let
 be time of xo yo zo - coordinate system.
be time of xo yo zo - coordinate system.Figure 0401
Since the value of speed of light is always 1 in all inertial frames of reference, equalities of spherical waves of light in two coordinate systems are expressed as follows, respectively:
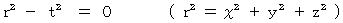
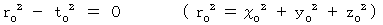
Therefore,
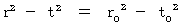
 (Equality 4-1)
(Equality 4-1)To simplify, we replace three-dimensional space with one-dimensional space; we express the x y z - coordinate system with r t - coordinate system, and express the xo yo zo - coordinate system with r o t o - coordinate system. the coordinate conversion from the r t - coordinate system to the ro to - coordinate system is expressed as follows by using 'linear function of vector', i.e. 'tensor.'
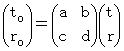
 (Equality 4-2)
(Equality 4-2)Therefore,
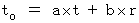
 (Equality 4-3)
(Equality 4-3)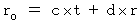
 (Equality 4-4)
(Equality 4-4)By applying (Equality 4-3) and (Equality 4-4) to (Equality 4-1), and then transforming, we obtain the following equality:
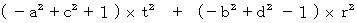
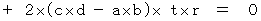
A necessary condition for this equality to consist of any combination of
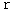 and
and 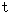 is as follows:
is as follows: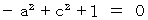
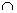
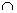
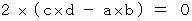
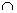 stands for intersection.
stands for intersection.Therefore,
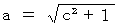
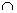
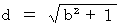
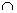
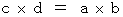
Therefore, (Equality 4-2) is expressed as follows:
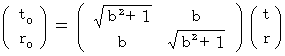
 (Equality 4-5)
(Equality 4-5)How is the movement of the origin of the

 -coordinate system expressed in the
-coordinate system expressed in the 
 -coordinate system ?
-coordinate system ?The answer is as follows:
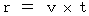
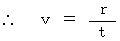
 (Equality 4-6)
(Equality 4-6)Next, let us think which space-time point of the
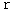
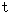 -coordinate system is converted into the origin of
-coordinate system is converted into the origin of 
 -coordinate system.
-coordinate system.By applying


 to (Determinant 4-5), we obtain the following equality:
to (Determinant 4-5), we obtain the following equality: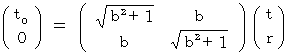
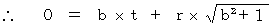
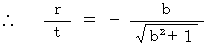
 (Equality 4-7)
(Equality 4-7)What does (Equality 4-7) mean ? It means as follows:
 If the space-time point with coordinates (
If the space-time point with coordinates ( 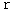 ,
, 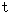 ) of the
) of the 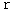
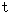 -coordinate system satisfies this equality, this space-time point is converted into the origin of the
-coordinate system satisfies this equality, this space-time point is converted into the origin of the 
 -coordinate system.
-coordinate system.
Therefore, we pile (Equality 4-7) on (Equality 4-6); both of them show the origin of

 -coordinate system. Then, we can say as follows:
-coordinate system. Then, we can say as follows: Any combination of
Any combination of 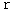 and
and 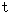 , which satisfy (Equality 4-6), must satisfy (Equality 4-7). So, the following equality must be valied:
, which satisfy (Equality 4-6), must satisfy (Equality 4-7). So, the following equality must be valied: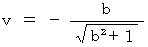
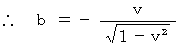
 (Equality 4-8)
(Equality 4-8) 
By applying (Equality 4-8) to (Equality 4-5), we obtain the following equality of the 'Lorenz transformation':
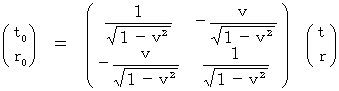
 (Equality 4-9)
(Equality 4-9)We obtain the following equality, by transforming (Equality 4-9) inversely:
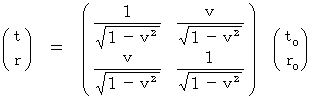
 (Equality 4-10)
(Equality 4-10)I call (Equality 4-10) 'inverse Lorentz transformation.'
I think that the 'inverse Lorentz transformation (Equality 4-10) ' is more important than the 'Lorenz transformation (Equality 4-9) ' The reason is as follows:
 What is important is not how I am observed by others but how I observe others. 'Lorenz transformation' is a coordinate conversion from an observed person to observing person.
What is important is not how I am observed by others but how I observe others. 'Lorenz transformation' is a coordinate conversion from an observed person to observing person.
Next, I show the simple method of finding 'Lorentz transformation.'
To simplify, we consider space as one dimension. There is the traveling coordinate systems
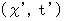 at a speed of
at a speed of  relative to the stationary coordinate systems
relative to the stationary coordinate systems 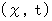 . Let us find the coordinate conversion from the latter to the former.
. Let us find the coordinate conversion from the latter to the former. When
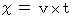 , it is
, it is 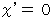 . Therefore, we can set the coordinate conversion on space as follows :
. Therefore, we can set the coordinate conversion on space as follows :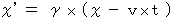
 (Equality 4-11)
(Equality 4-11)Since traveling is symmetric, we can set reverse coordinate conversion of (Equality 4-11) as follows :
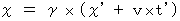
 (Equality 4-12)
(Equality 4-12)The equations of traveling of light, i.e. photon, in each coordinate system are expressed as follows :

 (Equality 4-13)
(Equality 4-13)We think about space-time points on which light transmits. They are shown as light cone which is like megaphone without inside space. We think about only these space points.
Plugging (Equality 4-13) into (Equality 4-11) or (Equality 4-12), we obtain the following equalities :
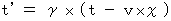
 (Equality 4-14)
(Equality 4-14)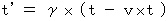
 (Equality 4-15)
(Equality 4-15) 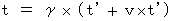
 (Equality 4-16)
(Equality 4-16) Owing to (Equality 4-15) and (Equality 4-16), we obtain the following equality :
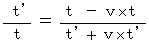
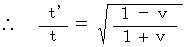
Owing to (Equality 4-15) , we obtain the following equality :
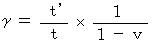
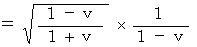
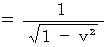
 (Equality 4-17)
(Equality 4-17)Plugging (Equality 4-17) into (Equality 4-11), we obtain the following equality :
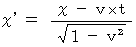
 (Equality 4-18)
(Equality 4-18) Plugging (Equality 4-17) into (Equality 4-14), we obtain the following equality :
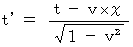
 (Equality 4-19)
(Equality 4-19)(Equality 4-18) and (Equality 4-19) show the coordinate conversion on space-time points on which light transmits.
We suppose that (Equality 4-18) and (Equality 4-19) also show the coordinate conversion on every space-time points on which light does not transmit. Then, (Equality 4-18) and (Equality 4-19) become equalities which show the coordinate conversion from the stationary coordinate systems
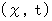 to the traveling coordinate systems
to the traveling coordinate systems 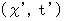 at a speed of
at a speed of  relative to the stationary coordinate systems. we call these equalities 'Equation of Lorentz transformation.'
relative to the stationary coordinate systems. we call these equalities 'Equation of Lorentz transformation.'