Chapter 5 Relation between Relative-Time and Absolute-Time
Relation between Relative-Time and Absolute-Time
When I see my daughter sleeping soundly, I think sometime what dream she is seeing. If I can see her dream on real time, it may be not the dream as it is. How does someone observe an object observed by another person? It is the 'Lorentz transformation' that replies to this question.
Three kinds of observers appear in this book. First, there is an observer who observes only stationary objects. We will call him/her 'the 0th observer.' Next, there is an observer who observes objects being observed by many 0th observers who keep linear uniform motion in various directions at various speeds. We will call him/her 'the 1st observer.' Last, there is an observer on linear uniform motion who observes objects being observed by the 1st observer. We will call him/her 'the 2nd observer.'
In this chapter, we study how an object observed by the 0th observer is observed by the 1st observer. For this purpose, we use the ' Lorentz transformation ' under the condition of 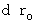

 ;
; 
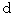
 of
of 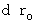 stands for the infinitesimal intervals.
stands for the infinitesimal intervals.
Now let us think how infinitesimal intervals of distance ( 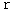 ) and time (
) and time ( 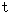 ) are converted with the 'Lorentz transformation.'
) are converted with the 'Lorentz transformation.'
Let (  ,
,  ) and (
) and ( 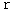 ,
, 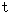 ) be coordinates of the 0th observer and coordinates of the 1st observer, respectively.
) be coordinates of the 0th observer and coordinates of the 1st observer, respectively.
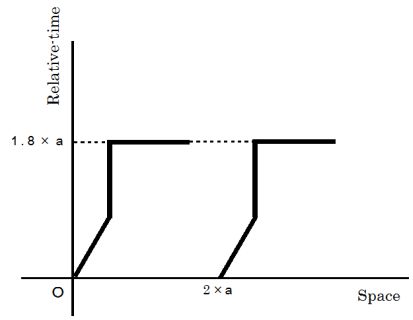
Then, 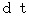 and
and  are expressed as follows :
are expressed as follows :
![]()
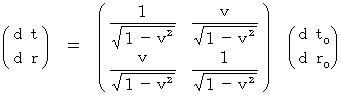
![]()
 (Equality 5-1)
(Equality 5-1)
Owing to (Equality 5-1) we obtain the following equality :
![]() ( d r ) 2 - ( d t ) 2 = ( d r 0 ) 2 - ( d t 0 ) 2
( d r ) 2 - ( d t ) 2 = ( d r 0 ) 2 - ( d t 0 ) 2
![]()
 (Equality 5-2)
(Equality 5-2)
Now, let us think about a statinary object in an inertial frame of reference moving at a speed of  . In other words, let us think about an object traveling with linear uniform motion at a speed of
. In other words, let us think about an object traveling with linear uniform motion at a speed of  . In another words, let us think about a stationary object for the 0th observer moving at a speed of
. In another words, let us think about a stationary object for the 0th observer moving at a speed of  relative to the 1st observer from the stand of view of the 1st observer .
relative to the 1st observer from the stand of view of the 1st observer .
A stationary object observed by the 0th observer keeps always 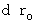

 .
.
When 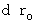

 , (Equality 5-1) is expressed with the following two equations :
, (Equality 5-1) is expressed with the following two equations :
![]()
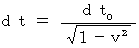
![]()
 (Equality 5-3)
(Equality 5-3)
![]()
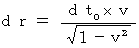
![]()
 (Equality 5-4)
(Equality 5-4)
We obtain the next equation owing to (Equality 5-3).
![]()
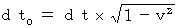
By applying this equation to (Equality 5-4), we obtain the following equality:
![]()
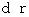


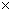
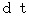
![]()
 (Equality 5-5)
(Equality 5-5)
Moreover, by substituting  for
for 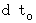 of (Equality 5-2), we obtain the next equality :
of (Equality 5-2), we obtain the next equality :
![]()
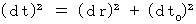
![]()
 (Equality 5-6)
(Equality 5-6)
(equality 5-1) and (Equality 5-2) 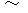 (Equality 5-6) are the answers for the question how a stationary object observed by the 0th observer is observed by the 1st observer traveling with linear uniform motion at a speed of
(Equality 5-6) are the answers for the question how a stationary object observed by the 0th observer is observed by the 1st observer traveling with linear uniform motion at a speed of  relative to the 0th observer.
relative to the 0th observer.
Well, I ask you as follows :


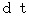
 is time intervals of the 1st observer observing multiple objects traveling with linear uniform motion in various directions and at various speeds.
is time intervals of the 1st observer observing multiple objects traveling with linear uniform motion in various directions and at various speeds. 
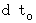
 is time intervals of the 0th observer observing only stationary objects. Which time is absolute? In other words, which time acts as paramater to rotate hands of a clock?
is time intervals of the 0th observer observing only stationary objects. Which time is absolute? In other words, which time acts as paramater to rotate hands of a clock?
The answer is  time of the 1st observer.
time of the 1st observer. It is natural that an observer in the center of his/her own world observes and recognizes many movenents of surrounding objects. ( In a religious world, to the contrary, an observer may be observed by a creator or an admired Deity in the center of the world. ) Therefore, time of the 1st observer is absolute, and it is a parameter for movements of all objects. On the other hand, time of the 0th observer is relative.
It is natural that an observer in the center of his/her own world observes and recognizes many movenents of surrounding objects. ( In a religious world, to the contrary, an observer may be observed by a creator or an admired Deity in the center of the world. ) Therefore, time of the 1st observer is absolute, and it is a parameter for movements of all objects. On the other hand, time of the 0th observer is relative.
To understand this statement, please see Figure 0501. This figure shows (Equality 5-6). 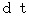 is the distance of the space-time point with coordinates of
is the distance of the space-time point with coordinates of 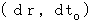 from the coordinate origin.
from the coordinate origin.
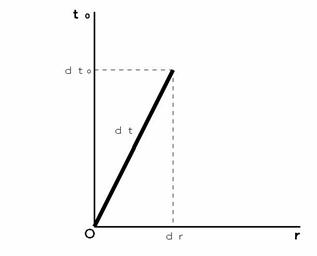
Please see Figure 0502. We see that there are many combinations of 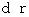 and
and 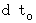 which make (Equality 5-6) valied.
which make (Equality 5-6) valied.
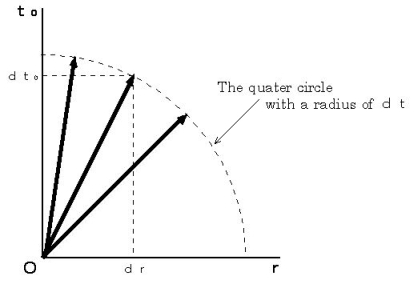
When an object keeps still with respect to an observer, it is 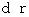

 , and the movement of the object is expressed with a vector just on to - axis.
, and the movement of the object is expressed with a vector just on to - axis.


 of (Equality 5-6) :
of (Equality 5-6) :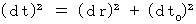 is called generally 'proper time.' Since it sounds like objective and absolute, I call it 'relative-time.' And I call
is called generally 'proper time.' Since it sounds like objective and absolute, I call it 'relative-time.' And I call 
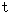
 'absolute-time.'
'absolute-time.'Relative-time is the time of the 0th observer ; it is observed by the 1st observer. That is, relative-time intervals are the time intervals through which the 0th observer traveling with the same velocity as an object traveling with liner uniform motion relative to the stationary 1st observer.
When the 0th observer keeps still relative to the 1st observer, relative-time intervals is equal to absolute-time intervals. It is the case under the condition of


 of (Equality 5-3) or
of (Equality 5-3) or 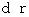

 of (Equality 5-6).
of (Equality 5-6).
Chapter 6 Epstein's Four-Dimensional Space-Time
Epstein's Four-Dimensional Space-Time
In Chapter 5, we studied how an object observed by the 0th observer is observed by the 1st observer. In this chapter, to the contrary, we study how an object observed by the 1st observer is observed by the 0th observer. It is clear that all objects keep still for the 0th observer, but let us study more deeply.First, please remember (Equality 5-6). We obtained owing to the 'modified Lorentz transformotion' under the conditon of
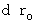

 . I show it again :
. I show it again :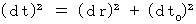
Second, please draw the coordinate which horizontal axis is the space of the 1st observer (
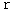 ) and which vertical axis is the absolute-time of the 0th observer (
) and which vertical axis is the absolute-time of the 0th observer ( ).
).{ Omission }
I call the four-dimensional space-time consists of three-dimensional space and one-dimensional relative-time 'Epstein's four-dimensional space-time.'
The 'Epstein's four-dimensional space-time' has four features as follows:
 The 1st observer is the main character of the observation.
The 1st observer is the main character of the observation. It consists of three-dimensional space and one-dimensional
It consists of three-dimensional space and one-dimensional At a superficial level, its coordinate system contain both the 1st
At a superficial level, its coordinate system contain both the 1st All objects are constantly moving in this four-dimensional
All objects are constantly moving in this four-dimensionalSince we must always check absolute-time acting as a parameter, I express the 'Epstein's four-dimensional space-time coordinate' with the following expression:
I will show the example of Epstein's space-time. To be simple, we consider space as one-dimension. The object A and the object B can change velocity at a moment. They travel or stand still with always the same velocity.
Space-time points on which they exist at the start of the observation are as follows :
![]() The object A :
The object A :![]()
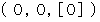
![]() The object B :
The object B :![]()
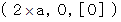
They travel in the positive direction at a speed of 60% of a light speed in the first  , and then they stand still in the next
, and then they stand still in the next  , and then they travel in the positive direction at a light speed in the last
, and then they travel in the positive direction at a light speed in the last  . Space-time points on which they exist at the end of the observation are as follows :
. Space-time points on which they exist at the end of the observation are as follows :
![]() The object A :
The object A :![]()
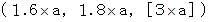
![]() The object B :
The object B :![]()
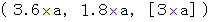
The traveling of them is shown with Epstein's space-time in Figure 0601.
Figure 0601
![]()
Length of the locus of an object shows absolute-time intervals in Epstein's space-time. We need space coordinate and absolute-time point to find the realistic space-time point on which an object exist, but we don't need relative-time point. In this sense, Epstein's four-dimensional space-time is a virtual space-time.
There are two objects which can change 'space velocity' in an instant. These objects start the same space point at the same time, and then travel through space with linear uniform motion.
Firstly, let us imagine Minkowski's four-dimensional space-time.
An elevator with wide space is going up at a constant speed. Two objects are traveling through space in the elevator at a free 'space velocity' on the condition that the magnitudes of velocities are in the range between
 and
and  . The time coordinates of space-time points on which they exist are always the same. With respect to X-coordinate and Y-coordinate of the 'space velocity' of an object, the sum of X-coordinate to the second power and Y-coordinate to the second power is equal or under
. The time coordinates of space-time points on which they exist are always the same. With respect to X-coordinate and Y-coordinate of the 'space velocity' of an object, the sum of X-coordinate to the second power and Y-coordinate to the second power is equal or under  . Please imagine the collision of these objects. It is the very collision in the elevator. That is, X-axis space coordinates, Y-axis space coordinates, and time-coordinates of space-time points on which they exist are the all same, respectively.
. Please imagine the collision of these objects. It is the very collision in the elevator. That is, X-axis space coordinates, Y-axis space coordinates, and time-coordinates of space-time points on which they exist are the all same, respectively.Secondly, let us imagine Epstein's four-dimensional space-time. Two objects are traveling through three-dimensional space-time at the constant and same speed of
 . Even if an object changes 'space velocity', it does not change 'space-time speed.' With respect to X-coordinate, Y-coordinate, and relative-time coordinate of the 'space-time velocity' of an object, the sum of X-coordinate to the second power, Y-coordinate to the second power, and relative-time coordinate to the second power is always equal to
. Even if an object changes 'space velocity', it does not change 'space-time speed.' With respect to X-coordinate, Y-coordinate, and relative-time coordinate of the 'space-time velocity' of an object, the sum of X-coordinate to the second power, Y-coordinate to the second power, and relative-time coordinate to the second power is always equal to  . Please imagine the collision of these objects. They collide when X-axis space coordinates and Y-axis space coordinates of space-time points on which they exist are the all same, respectively, regardless of difference of relative-time coordinates of space-time points on which they exist.
. Please imagine the collision of these objects. They collide when X-axis space coordinates and Y-axis space coordinates of space-time points on which they exist are the all same, respectively, regardless of difference of relative-time coordinates of space-time points on which they exist.{ Omission }
Maxwell's equations show the four relationships between electric field and magnetic field. These relationships are satisfied in all inertial frames of reference. It leaded to the discovery of the form of a coordinate conversion. It is Lorenz transformation. A coordinate conversion is the mapping of one-to-one correspondence of space-time points of two coordinate systems. An object travels through four-dimensional space-time while keeping transferring a space-time point. Therefore, the realistic transformation on traveling of an object must be a coordinate conversion of space-time points on which the object exists.
To be simple, we consider space is one-dimension of X-axis. Mis. B is traveling in the negative direction of X-axis with a speed of
 with respect to Mr. A. The coordinate conversion from Mr. A's coordinate system to Mis. B's coordinate system is shown as follows :
with respect to Mr. A. The coordinate conversion from Mr. A's coordinate system to Mis. B's coordinate system is shown as follows :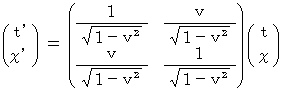
I call this expression 'reverse Lorentz transformation.'
Owing to 'Lorentz transformation' or 'reverse Lorentz transformation', we obtain the following equality :
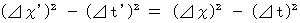
This equality shows 'law of constancy of four-dimensional space-time intervals regardless of a coordinate conversion with respect to four-dimensional space-time in which time is imaginary number.' We must express this equality exactly as follows :
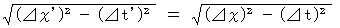
It may be called 'Law of constancy of proper time intervals regardless of a coordinate conversion', too. Depending on the values of
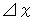 and
and  , this expression takes a value of imaginary number. The area of apace-time points, on which an object, which passes the space-time origin, can exist, is inside of light cone in the Minkowski four-dimensional space-time. The area of inside of the light cone is called 'area of time like.' In this area, it is
, this expression takes a value of imaginary number. The area of apace-time points, on which an object, which passes the space-time origin, can exist, is inside of light cone in the Minkowski four-dimensional space-time. The area of inside of the light cone is called 'area of time like.' In this area, it is 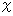
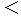
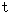 . The area of outside of the light cone is called 'area of space like.'
. The area of outside of the light cone is called 'area of space like.'Now, let us think about a coordinate conversion of space-time points on the borderline of 'area of time like' and 'area of space like'.
In Mr. A's coordinate system, a photon on one space point will travel for
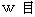 .
.Let
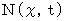 be the space-time point on which the photon exists at the start of the observation.
be the space-time point on which the photon exists at the start of the observation.Let
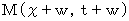 be the space-time point on which the photon exists at the end of the observation.
be the space-time point on which the photon exists at the end of the observation.We find the following equality :
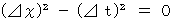
Owing to this equality, we obtain the following equality :
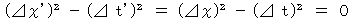
 (Equality 6-1)
(Equality 6-1)Let us see the following equality is satisfied :
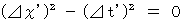
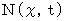 and
and  in Mr. A's coordinate system are converted to Mis. B's coordinate system to be as follows, respectively :
in Mr. A's coordinate system are converted to Mis. B's coordinate system to be as follows, respectively :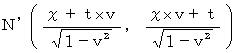
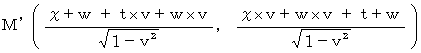
So, square of space-time intervals between
 and
and  are as follows :
are as follows :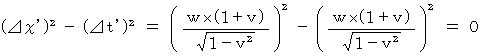
It is why, (Equality 6-1) is satisfied.
Let us make it be simpler. We make space-time intervals be one between a space-time point and the space-time origin. We change coordinates of the space-time point
 and the space-time point
and the space-time point  as follows :
as follows :
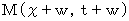

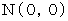

Therefore, (Equality 6-1) is expressed as follows :
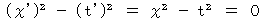
 (Equality 6-2)
(Equality 6-2)Please do not forget that this equality is satified with respect to only space-time points on which electromagnetic wave emitted from space-time origin can exist.
I think as follow :
 Lorentz transformation makes principle of relativity hold good to electromagnetic field. Plus, it shows the change of traveling of electromagnetic wave in two coordinate systems. It never shows, however, the change of traveling of an object in two coordinate systems. But, Lorentz transformation is used as such tool to produce a lot of contradictions.
Lorentz transformation makes principle of relativity hold good to electromagnetic field. Plus, it shows the change of traveling of electromagnetic wave in two coordinate systems. It never shows, however, the change of traveling of an object in two coordinate systems. But, Lorentz transformation is used as such tool to produce a lot of contradictions.
I explain it. Please see (Equality 6-2). In Mr. A's coordinate system, space-time points, on which a photon, which has passed the space-time origin, can exist, are shown as
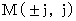 . Therefore, the idea struck my mind; the idea is as follow :
. Therefore, the idea struck my mind; the idea is as follow : Lorentz transformation comes from the principle of relativity on relationship between electric field and magnetic field, i.e. Maxwell equations. Space point
Lorentz transformation comes from the principle of relativity on relationship between electric field and magnetic field, i.e. Maxwell equations. Space point 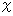 and time point
and time point 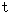 in Maxwell equations are not optional, and their relationship is shown as
in Maxwell equations are not optional, and their relationship is shown as  .
.Therefore, Lorentz transformation shows only the change of traveling of electromagnetic wave in two coordinate systems. It does not show the change of traveling of an object in two coordinate systems.

(Equality 6-2) is expressed as follows, too :
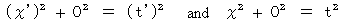
We consider
 of this equality as 'relative time' through which the photon travels; actually photon does not travel through relative time. Moreover, we consider an object travels through relative time. Let
of this equality as 'relative time' through which the photon travels; actually photon does not travel through relative time. Moreover, we consider an object travels through relative time. Let  be relative time intervals. We suppose that the following equality is satisfied :
be relative time intervals. We suppose that the following equality is satisfied :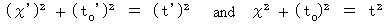
And then, we suppose that the following equality is satisfied :
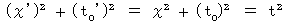
This supposed equality is just the root of my misunderstanding on the theory of relativity.
Chapter 7 Composition of velocities
Composition of velocities
In this chapter, we study how the 2nd observer observes an object observed by the 1st observer.
(1) Composition of two velocities of the same or opposite direction
Please imagine ; you are observing that a ball goes straight away at a speed of 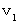 , and your friend traveling with linear uniform motion at a speed of
, and your friend traveling with linear uniform motion at a speed of 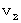 in the opposite direction of the ball relative to you. How does your friend observe the movement of the ball? I described in Chapter 1 that Figure 0103 is wrong.
in the opposite direction of the ball relative to you. How does your friend observe the movement of the ball? I described in Chapter 1 that Figure 0103 is wrong.
Now, I will show the correct answer. We repeat coordinate coversion expressed with (Equality 5-1) twice under the condition of 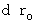

 . Then, we see how the 2nd observer observes an object observed by the 0th observer. In other words, we see how the 2nd observer observes an object observed by the 1st observer.
. Then, we see how the 2nd observer observes an object observed by the 0th observer. In other words, we see how the 2nd observer observes an object observed by the 1st observer.
Let 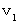 be a speed of the 1st observer relative to the 0th observer.
be a speed of the 1st observer relative to the 0th observer.
Let 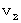 be a speed of the 2nd observer relative to the 1st observer.
be a speed of the 2nd observer relative to the 1st observer.
Let 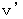 be a speed of the object observed by the 2nd observer.
be a speed of the object observed by the 2nd observer.
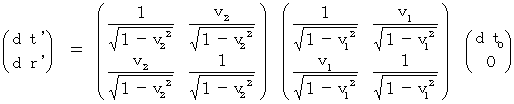
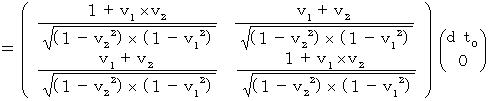
By dividing 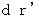 by
by 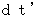 , we obtain
, we obtain 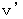 as follows :
as follows :
![]()
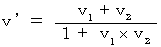
![]()
 (Equality 7-1)
(Equality 7-1)
The 'principle of constancy of the speed of light' means that all of the following three propositions are true :


 with repsect to all observers.
with repsect to all observers.
 .
.We must interpret
 rightly as follows:
rightly as follows: The speed of photon emitted from a stationary light source is
The speed of photon emitted from a stationary light source is  . Plus, composition of speeds follows (Equality 7-1). Therefore, the speed of photon emitted from a light source is
. Plus, composition of speeds follows (Equality 7-1). Therefore, the speed of photon emitted from a light source is  regardless of a velocity of the light source.
regardless of a velocity of the light source.
In contrast, we must not interpret
 as follows:
as follows: On the one hand, a bullet is shot from a traveling point, on the other hand, photon is emitted from a stationary space-time point on a coordinate system of an observer.
On the one hand, a bullet is shot from a traveling point, on the other hand, photon is emitted from a stationary space-time point on a coordinate system of an observer.
The reason why this interpretation is wrong is that the theory of relativity is a theory to unite a traveling of light and a traveling of an object. If we interpret as this, we can not object to the objection as follows :
 The form of a traveling of an object is different from the form of a traveling of light. Therefore, Lorentz transformation does not apply to a traveling of an object. Because, it comes from 'Vibration of photon on electromagnetic field' and 'Traveling of photon with proper speed'; Behavior of photon is 'Vibration on electromagnetic field', 'Vibration on electromagnetic wave', 'Traveling with proper speed', and 'Character as quantum.'
The form of a traveling of an object is different from the form of a traveling of light. Therefore, Lorentz transformation does not apply to a traveling of an object. Because, it comes from 'Vibration of photon on electromagnetic field' and 'Traveling of photon with proper speed'; Behavior of photon is 'Vibration on electromagnetic field', 'Vibration on electromagnetic wave', 'Traveling with proper speed', and 'Character as quantum.'
We must object to the objection like as follows :
 I must admit there is a certain logic in what you say. If we remodel Lorentz transformation, that is, we get absolute time back, we can unify the form of a traveling of photon and the form of a traveling of an object.
I must admit there is a certain logic in what you say. If we remodel Lorentz transformation, that is, we get absolute time back, we can unify the form of a traveling of photon and the form of a traveling of an object.
By the way, Michelson-Morley experiment and working out Lorentz transformation in Einstein's first thesis on relativity is before establishment of principle of constancy of the speed of light. Therefore, they use 'composition of speeds with Galilean transformation in Newtonian mechanics.' So, it is wrong that someone denies the theory of relativity by referring to these compositions of speeds.
When we consider that light travels through ether as medium at a speed of
 , we can say as follows :
, we can say as follows : :
: with respect to an observer standing still with respect to ether.
with respect to an observer standing still with respect to ether. :
: with respect to ether, the speed of light traveling in this direction is
with respect to ether, the speed of light traveling in this direction is 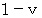 .
. with respect to a stationary observer, as medium at a speed of
with respect to a stationary observer, as medium at a speed of  in the opposite direction.
in the opposite direction. :
: with respect to ether for Mr. A standing still with respect to ether is
with respect to ether for Mr. A standing still with respect to ether is 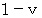 .
. , and the speed of Ms. B with respect to Mr. A is
, and the speed of Ms. B with respect to Mr. A is  .
.Please notice that values of the speed of
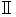 and
and  are the same. A speed for an objective observer and a speed for a subjective observer are the same in Newtonian mechanics.
are the same. A speed for an objective observer and a speed for a subjective observer are the same in Newtonian mechanics.These items are rewritten in relativity as follows :
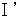 :
: with respect to all observers.
with respect to all observers.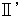 :
: with respect to an observer traveling at a speed of
with respect to an observer traveling at a speed of  with respect to the light source.
with respect to the light source.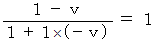
 :
: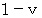 .
.I will state the following gist in Chapter 9, Chapter 11, and Chapter 12 :

 is a speed of the third party. It is unnecessary and harmful in the theory of relativity. A speed of the third party is just a speed in a vision which makes the theory of relativity be confused.
is a speed of the third party. It is unnecessary and harmful in the theory of relativity. A speed of the third party is just a speed in a vision which makes the theory of relativity be confused.
(2) Composition of two velocities of the perpendicular direction
{ Omission }
A monster says:
 When an object B is thrown out from a traveling object A in the perpendicular direction to the movement of the object A , whether the object A is approaching an observer or going away from the observer, the perpendicular speed of the object B relative to the observer gets slower than the speed observed by another observer moving with the same velocity as the object A . In short, vertical time of an object traveling in the horizontal direction passes more slowly than that of a stationary object.
When an object B is thrown out from a traveling object A in the perpendicular direction to the movement of the object A , whether the object A is approaching an observer or going away from the observer, the perpendicular speed of the object B relative to the observer gets slower than the speed observed by another observer moving with the same velocity as the object A . In short, vertical time of an object traveling in the horizontal direction passes more slowly than that of a stationary object.
So, let us ask the Monster the following question:
 We can not understand that only vertical time passes slower, because time is one-dimension. How about thinking that vertical space is extended? We think the result is the same as your view.
We can not understand that only vertical time passes slower, because time is one-dimension. How about thinking that vertical space is extended? We think the result is the same as your view.
Just then he says :
 Ha-ha, foolish human beings! Your view fits into the trap. Listen to me carefully. Imagine that two rings of the same size are approaching face to face at high speed in the horizontal direction, and then they collid under your very nose. If this situation is observed by the other observer moving at the same velocity as the right ring, the left ring passes through the outside of the right ring without collision. If this situation is observed by the other observer moving at the same velocity as the left ring, the right ring passes through the outside of the left ring without collision. Have you noticed? You always label everthing 'good' or 'bad' selfishly, but everything is originally
Ha-ha, foolish human beings! Your view fits into the trap. Listen to me carefully. Imagine that two rings of the same size are approaching face to face at high speed in the horizontal direction, and then they collid under your very nose. If this situation is observed by the other observer moving at the same velocity as the right ring, the left ring passes through the outside of the right ring without collision. If this situation is observed by the other observer moving at the same velocity as the left ring, the right ring passes through the outside of the left ring without collision. Have you noticed? You always label everthing 'good' or 'bad' selfishly, but everything is originally  .
.
I call
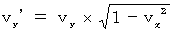 'Law of relative vertical speed.'
'Law of relative vertical speed.'Now, let us do thought experiment to confirm 'Law of relative vertical speed.' Please imagine that the object A is traveling at a speed of
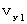 with respect to the 1st observer. The object A passes through space-time origin of the 1st observer's coordinate system. The object A is traveling in the direction of Y-axis. Let
with respect to the 1st observer. The object A passes through space-time origin of the 1st observer's coordinate system. The object A is traveling in the direction of Y-axis. Let 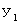 be the position of the object A at a time point of
be the position of the object A at a time point of 
 . We obtain the following equation :
. We obtain the following equation :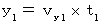

The 2nd observer is traveling at a speed of
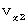 with respect to the 1st observer in the direction of X-axis. Space-time origins of them are identical. We consider that the movement of the object A with respect to the 2nd observer is expressed with following equations :
with respect to the 1st observer in the direction of X-axis. Space-time origins of them are identical. We consider that the movement of the object A with respect to the 2nd observer is expressed with following equations :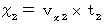
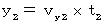
Let us find how
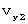 is expressed with
is expressed with 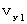 and
and 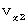 .
.The coordinate conversion from the 2nd observer to the 1st observer is expressed with following equalities of Lorentz transformation :
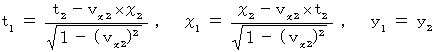
Plugging these equations to (Equality 7-5), we obtain the following equation:
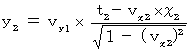
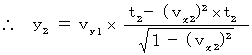
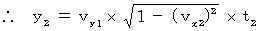
Therefore, we obtain the following equation :
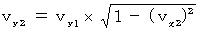
This equation shows that the speed of the object A in the direction of Y-axis with respect to the 2nd observer is as follows :
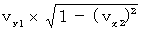
Therefore, the speed of the object A with respect to the 2nd observer
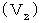 is expressed as follows :
is expressed as follows :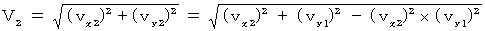
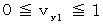 and
and 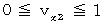 , it is
, it is 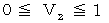 .
.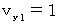 or
or 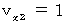 , it is
, it is 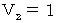 .
.
Chapter 8 Coordinate Conversion of Epstein's Four-Dimensional Space-Time
Coordinate Conversion of Epstein's Four-Dimensional Space-Time
Notice : A coordinate conversion from ' the coordinate system of the 1st observer traveling at a speed of
A coordinate conversion from ' the coordinate system of the 1st observer traveling at a speed of 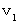 relative to the 0th observer ' to ' the coordinate system of the 2nd observer traveling at a speed of
relative to the 0th observer ' to ' the coordinate system of the 2nd observer traveling at a speed of 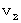 relative to the 1st observer in the opposite direction to the movement direction of the 0th observer relative to the 1st observer '
relative to the 1st observer in the opposite direction to the movement direction of the 0th observer relative to the 1st observer '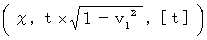

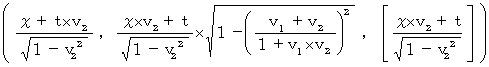
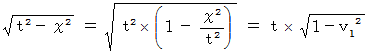
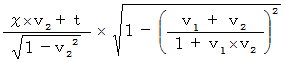
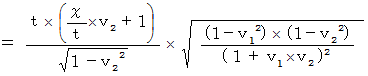
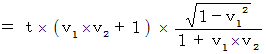
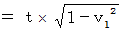
 A coordinate conversion from ' the coordinate system of the 1st observer traveling at a speed of
A coordinate conversion from ' the coordinate system of the 1st observer traveling at a speed of 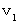 relative to the 0th observer ' to ' the coordinate system of the 2nd observer traveling at a speed of
relative to the 0th observer ' to ' the coordinate system of the 2nd observer traveling at a speed of 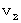 relative to the 1st observer in the perpendicular direction to the movement direction of the 0th observer relative to the 1st observer '
relative to the 1st observer in the perpendicular direction to the movement direction of the 0th observer relative to the 1st observer '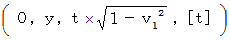

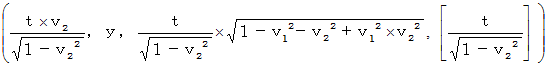
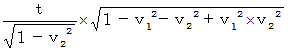
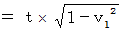
Chapter 9 Relativity of Simultaneity of two events on different space points
Relativity of Simultaneity of two events on different space points
Figure 0901 shows the 1st observer's coordinate.Figure 0901
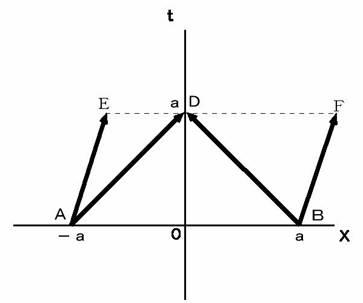
 : The locus vector of light emitted from the light source A
: The locus vector of light emitted from the light source A
 : The locus vector of light emitted from the light source B
: The locus vector of light emitted from the light source B
 : The locus vector of the light source A
: The locus vector of the light source A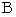
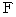 : The locus vector of the light source B
: The locus vector of the light source B
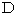 : The locus vector of the 1st observer
: The locus vector of the 1st observerFigure 0902 shows how the 2nd observer traveling at a speed of
 relative to the 1st observer observes this situation.
relative to the 1st observer observes this situation.We obtained the coordinates of the point
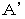 , the point
, the point 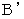 , and the point
, and the point 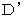 owing to the 'diterminant of Lorentz transformation.'
owing to the 'diterminant of Lorentz transformation.'Fig.0902
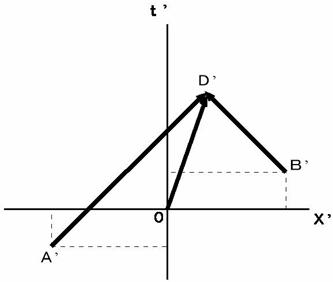
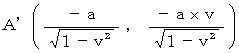
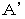
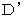 : The locus vector of light
: The locus vector of light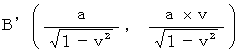
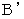
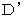 : The locus vector of light
: The locus vector of light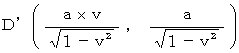
 : The locus vector of the 1st observer
: The locus vector of the 1st observerOwing to this figure we see that the 2nd observer observes two light sources emit light at different time points and he/she observes two emitted lights reach the 1st observer on the space-time point
 simultaneously.
simultaneously.As above statement, the simultaneity is disappeared as a result of a coordinate conversion. My way of explanation on the simultaneity is different from an established theory. The established theory uses a coordinate conversion from the 2nd observer to the 1st observer. The established theory explains the relativity of simultaneity by comparing 'the collision of a flash emitted from a traveling light source and the 2nd observer' and 'the collision of the flash and the 1st observer traveling with the same velocity as the light source'.
The established theory uses a woman sitting in the middle of a traveling train and a man sitting on a platform. Before my explanation, please remember the following mentions


The established theory is as follows:
The man on a platform, who is the 2nd observer, says as follows

 Two flashes, which came from both end of the train, are shot simultaneously with respect to me, because they are shot at the same distance away from me and they reach me at the same time. Like this, two flashes seem to be shot simultaneously with respect to her. My objective observation, however, denies this. I show the reason as follows
Two flashes, which came from both end of the train, are shot simultaneously with respect to me, because they are shot at the same distance away from me and they reach me at the same time. Like this, two flashes seem to be shot simultaneously with respect to her. My objective observation, however, denies this. I show the reason as follows 
 In my coordinate system, a flash from a light source on the front of the train and a flash from a light source on the back of the train are shot simultaneously. They reach me at the same time.
In my coordinate system, a flash from a light source on the front of the train and a flash from a light source on the back of the train are shot simultaneously. They reach me at the same time. In my coordinate system, 'the space intervals between the space point on which the flash from the light source on the front of the train is shot and the space point on which the flash reached her' are shorter than 'the space intervals between the space point on which the flash from the light source on the back of the train is shot and the space point on which the flash reached her.'
In my coordinate system, 'the space intervals between the space point on which the flash from the light source on the front of the train is shot and the space point on which the flash reached her' are shorter than 'the space intervals between the space point on which the flash from the light source on the back of the train is shot and the space point on which the flash reached her.' Owing to
Owing to  and
and  , in my coordinate system, she collides with two flashes at a different time point, i.e. at separate time.
, in my coordinate system, she collides with two flashes at a different time point, i.e. at separate time. In her coordinate system, she collides with two flashes at a different time point, i.e. at separate time, because state of action of an object and situation of collision etc. are constant regardless of coordinate conversions.
In her coordinate system, she collides with two flashes at a different time point, i.e. at separate time, because state of action of an object and situation of collision etc. are constant regardless of coordinate conversions.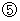 Both in my coordinate system and in her coordinate system, 'the space intervals between the space point on which the light source on the front of the train exists and the space point on which she exists' are always the same length as 'the space intervals between the space point on which the light source on the back of the train exists and the space point on which she exists.'
Both in my coordinate system and in her coordinate system, 'the space intervals between the space point on which the light source on the front of the train exists and the space point on which she exists' are always the same length as 'the space intervals between the space point on which the light source on the back of the train exists and the space point on which she exists.'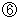 In her coordinate system, the space point on which a flash is shot is the same as the space point on which a light source exists.
In her coordinate system, the space point on which a flash is shot is the same as the space point on which a light source exists.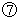 Therefore, in her coordinate system, 'the space intervals between the space point on which the flash from the light source on the front of the train is shot and the space point on which the flash reached her' are the same length as 'the space intervals between the space point on which the flash from the light source on the back of the train is shot and the space point on which the flash reached her.'
Therefore, in her coordinate system, 'the space intervals between the space point on which the flash from the light source on the front of the train is shot and the space point on which the flash reached her' are the same length as 'the space intervals between the space point on which the flash from the light source on the back of the train is shot and the space point on which the flash reached her.'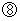 Owing to
Owing to  and
and 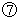 , in her coordinate system, a flash from a light source on the front of the train and a flash from a light source on the back of the train are shot at a separate time.
, in her coordinate system, a flash from a light source on the front of the train and a flash from a light source on the back of the train are shot at a separate time. 
Now, I coment on the
 relativity of simultaneity of two events on different space points
relativity of simultaneity of two events on different space points .
.Firstly, I refer that we think mistakenly that we find the evidence of mistake on the 'principle of constancy of ligth velocity' in an explanation of the established theory. It is as follows:
 For the man on the platform, the value of time intervals while the light emitted from the front of the train reaches the woman on the train is smaller than the value of the space intervals of the half of the train. ( Proviso : We use the
For the man on the platform, the value of time intervals while the light emitted from the front of the train reaches the woman on the train is smaller than the value of the space intervals of the half of the train. ( Proviso : We use the 
 system of units.
system of units. ) That is,
) That is,  with respect to the woman on the train, the light emitted from the front of the train reaches herself through the space intervals of the same value as the space intervals of the half of the train, while spending time intervals of the smaller value than the value of the space intervals of the half of the train.
with respect to the woman on the train, the light emitted from the front of the train reaches herself through the space intervals of the same value as the space intervals of the half of the train, while spending time intervals of the smaller value than the value of the space intervals of the half of the train. Therefore, 'principle of constancy of ligth velocity' is a serious mistake. Because, with respect to the woman on the train, the light travels at a speed of more than
Therefore, 'principle of constancy of ligth velocity' is a serious mistake. Because, with respect to the woman on the train, the light travels at a speed of more than  .
.
This misunderstanding is very important to understand the theory of relativity. Certainly, the man on the platform seems to observe so. We ready to say as follows:
 The collaboration of the speed of light and the speed of the train makes the value of the speed of light with respect to the woman on the train more than
The collaboration of the speed of light and the speed of the train makes the value of the speed of light with respect to the woman on the train more than  .
.
Come to think of it frome a viewpoint of the woman on the train, however, we see the speed of light with respect to her is certainly
 .
.Above-mentioned misunderstanding must be criticized as follows :
 Just because it is
Just because it is  With respect to the man on the platform, the light reaches the woman on the train at a speed of
With respect to the man on the platform, the light reaches the woman on the train at a speed of  through the space intervals of the smaller value than the value of the space intervals of the half of the train, while spending time intervals of the smaller value than the value of the space intervals of the half of the train.
through the space intervals of the smaller value than the value of the space intervals of the half of the train, while spending time intervals of the smaller value than the value of the space intervals of the half of the train. , it is not necessarily
, it is not necessarily  With respect to the woman on the train, the light reaches her through the space intervals of the same value as the space intervals of the half of the train, while spending time intervals of the smaller value than the value of the space intervals of the half of the train.
With respect to the woman on the train, the light reaches her through the space intervals of the same value as the space intervals of the half of the train, while spending time intervals of the smaller value than the value of the space intervals of the half of the train.

That is as follows :
 Time intervals while light trravels belongs to the coordinate system of the the man on the platform, in spite of the declaration of
Time intervals while light trravels belongs to the coordinate system of the the man on the platform, in spite of the declaration of with respect to the woman on the train
with respect to the woman on the train . If we try to find the contents of the observation of the person on the train, we must use the coordinate system of the person on the train.
. If we try to find the contents of the observation of the person on the train, we must use the coordinate system of the person on the train.
We use the following equation to find the relative speed from a standpoint of a third party :
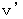

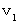
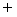
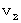
We use the following equation to find the realistic speed from a standpoint of a person concerned :
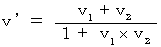
The composition of speeds means a coordinate conversion of a speed.
The theory of relativity serves us the following lesson :
 We must observe from a viewpoint of a person concerned, because we can not observe in detail from a viewpoint of a third party.
We must observe from a viewpoint of a person concerned, because we can not observe in detail from a viewpoint of a third party.
By the way, if the following statements are true, it makes the observation of the 2nd observer consistent. However, I regret to say that the following statements break the principle of constancy of the speed of light.
 The speed of the flash from the light source on the front of the train which reaches the 2nd observer with respect to the 2nd observer :
The speed of the flash from the light source on the front of the train which reaches the 2nd observer with respect to the 2nd observer :
 The speed of the flash from the light source on the front of the train which reaches the 1st observer with respect to the 2nd observer :
The speed of the flash from the light source on the front of the train which reaches the 1st observer with respect to the 2nd observer :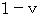
 The speed of the flash from a light source on the back of the train which reaches the 2nd observer with respect to the 2nd observer :
The speed of the flash from a light source on the back of the train which reaches the 2nd observer with respect to the 2nd observer :
 The speed of the flash from a light source on the back of the train which reaches the 1st observer with respect to the 2nd observer :
The speed of the flash from a light source on the back of the train which reaches the 1st observer with respect to the 2nd observer :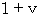
The speed of litht is constantly
 , regardless of observers traveling with various velocities with respect to a light source. Therefore, two lights emitted simultaneously at the same distance away from a stationary observer reach the observer at the same time without fail. So, if an observer sees simultaneously two lights emitted at the same distance away from the observer in the observer's coordinate system in which the observer stands still, we see that two lights were emitted simultaneously with respect to the observer. However, if we think about the case that the 2nd observer observes the 1st observer observing the light, it is not so.
, regardless of observers traveling with various velocities with respect to a light source. Therefore, two lights emitted simultaneously at the same distance away from a stationary observer reach the observer at the same time without fail. So, if an observer sees simultaneously two lights emitted at the same distance away from the observer in the observer's coordinate system in which the observer stands still, we see that two lights were emitted simultaneously with respect to the observer. However, if we think about the case that the 2nd observer observes the 1st observer observing the light, it is not so.Secondly, I refer that we don't try to find whether an observer recognizes simultaneity or not. We must find whether two events occur simultaneously or not.
The 'simultaneity' does not mean 'simultaneous recognition' but means 'simultaneous event.' If we take the 'simultaneous recognition', we mistakenly consider as follows:
 It is
It is the condition for an observer to observe that another person brinks at the same time as the observer brinks
the condition for an observer to observe that another person brinks at the same time as the observer brinks that another person with the distance from the observer of
that another person with the distance from the observer of  brinks
brinks  earlier than the observer brinks.
earlier than the observer brinks. 
Actually, when two persons brinks at the same time, they recognize each other that another person brinks after a brink of oneself. The relativity does not mention how information is given to an observer and how it is recognized by him/her. Because, it is not an epistemological theory but a physical theory; an epistemological theory asks for acknowledgments of an observer, a physical theory asks for objective existence and phenomenon in observer's space-time. Therefore, to prove the 'relativity of simultaneity', we only have to show the 'Lorentz transformation.' My explanation must takes away locuses of lights and the 1st observer.
Finally, I refer that the 'relativity of simultaneity of two events on different space points' is an unrealistic phenomenon. I show the following thought experiment, because I want you to understand it.
Please imagine a platform of a station in the country at night. An express is passing through the station. A man is waiting for the next local train on the platform. A woman is driving on a side road of the platform in the opposite direction of the traveling express. Just when the man, the woman, and the middle of the express are on a line, two clocks on both ends of the express flash. The man is the 1st observer in Figure 0901. The woman is the 2nd observer in Figure 0902. The man finds simultaneously that two clocks show
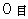 . When the woman observes this situation, she thinks as follows to fit into a maze
. When the woman observes this situation, she thinks as follows to fit into a maze 
 It is right that the man found simultaneously that two clocks indicate
It is right that the man found simultaneously that two clocks indicate 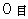 as he says.
as he says. But, on my observation as Figure 0902, both of two clocks did not flash at
But, on my observation as Figure 0902, both of two clocks did not flash at 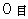 . Two flashes do not reach me simultaneously. The flash, which reached me first, flashed before
. Two flashes do not reach me simultaneously. The flash, which reached me first, flashed before 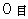 . Therefore, the clock is fast. The flash, which reached me second, flashed after
. Therefore, the clock is fast. The flash, which reached me second, flashed after 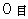 . Therefore, the clock is slow. It is the 'relativity of simultaneity.'
. Therefore, the clock is slow. It is the 'relativity of simultaneity.' Oh! Calm down! Let's look at things from a different angle. The difference of the observation between the 1st observer and the 2nd observer, i.e. me, is only the speed of the train. I am the 1st observer at the same time. Therefore, my observation is the same as Figure 0901 except for the speeds of clocks, isn't it?
Oh! Calm down! Let's look at things from a different angle. The difference of the observation between the 1st observer and the 2nd observer, i.e. me, is only the speed of the train. I am the 1st observer at the same time. Therefore, my observation is the same as Figure 0901 except for the speeds of clocks, isn't it? The 1st observer traveling with respect to me stands still with respect to himself. So, let us place the figure, in which the 1st observer stands still, on the figure, in which the 2nd observer, i.e. me, stands still. Then, speeds of the train are different. And, two clocks flash simultaneously with respect to both of us, and then two flashes, which have correct information that the clock flashed at
The 1st observer traveling with respect to me stands still with respect to himself. So, let us place the figure, in which the 1st observer stands still, on the figure, in which the 2nd observer, i.e. me, stands still. Then, speeds of the train are different. And, two clocks flash simultaneously with respect to both of us, and then two flashes, which have correct information that the clock flashed at  , reach us at
, reach us at  simultaneously, because light travels at a constant speed in all inertial frame of reference, regardless of the speed of light source.
simultaneously, because light travels at a constant speed in all inertial frame of reference, regardless of the speed of light source.
Chapter 10 Example of Coordinate Conversion of Four-Dimensional Space-Time
Example of Coordinate Conversion of Four-Dimensional Space-Time
To make sketches be easy, we consider that four-dimensional space-time is three-dimensional space-time with two-dimensional space.(1) Coordinate system of the 1st observer
( Question No.1 )
The object A and the object B are standing still. At a moment the object A emits light, and then the light reaches the object B. Please show the situation with Epstein's space-time in Figure 1001. Please consider these objects are on Y-axis of space.
( Answer )
Figure 1001
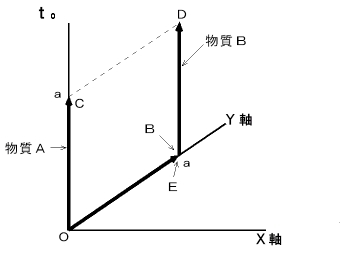
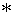
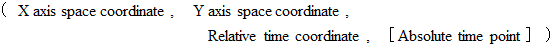
(2) Coordinate system of the 2nd observer
( Question No.2 )
The 2nd observer is traveling at a speed of v with respect to the 1st observer. Please show the observation of the 2nd observer in Figure 1002.
( Answer )
Figure 1002
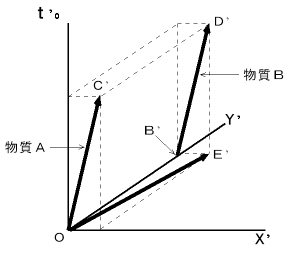
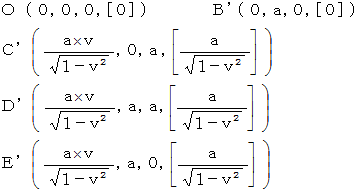
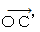 and the magnitude of
and the magnitude of 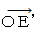 are
are 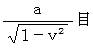 .
.