(1) 2でも5でもない素数
-
2でも5でもない素数の一の位の数は、 5以外の奇数です。 5以外の奇数は 1 から 9 までのどの自然数をかけても一の位が0の数にはなりません。 したがって、 2でも5でもない素数は 10n ( n は自然数 ) の約数ではありません。 したがって、 2でも5でもない素数の逆数は有限小数ではありません。
フェルマーの小定理 :
「 素数 b と b の倍数でない整数 a があるとき、 ab −1 を b で割った余りは 1 である。」
2でも5でもない素数は10の約数ではありません。 したがって、 フェルマーの小定理より、 次の命題は真になります。
「 Pが2でも5でもない素数であれば、 10P −1− 1 は P で割り切れる。 」
したがって、 Pが2でも5でもない素数であるとき 1 / P は循環小数になります。 その理由については、 十進BASIC > 十進BASIC_算数 > 循環小数に変換 をご覧ください。 なお、 循環小数でない無限小数は、 有理数ではなく無理数です。
十進BASIC のプログラムで確かめてみましょう :
-
「 K = 2m × 5n ( m と n は 0以上の整数 ) ならば、 1/K は有限小数である。」
という命題が真であることを証明しましょう。
m ≦ n のとき

m > n のとき
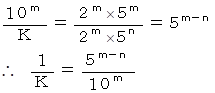
「 1/K = L / 10 n ( L と n は 自整数 ) ならば、 1/K は有限小数である。」
という命題は真ですので、 1/K は有限小数であることが判りました。
ちなみに、 「 K が自然数であり、 かつ、 1/K が有限小数であるならば、 K は 2m × 5n ( m と n は 0以上の整数 ) の形に素因数分解できる。」 という逆の命題も真です。 ただし、 「 L が有限小数であるならば、 1 / L は 2m × 5n ( m と n は 0以上の整数 ) の形に素因数分解できる。」 という命題は偽です。 なぜなら、 L = 0.3 のとき 1 / L = 3.3333・・・ だからです。
プログラムの内容 :
 数理論 へ戻る
数理論 へ戻る