列車の固有長 ：　

　　　トンネルの固有長 ：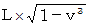　

　 列車の固有長の方がトンネルの固有長よりも長いのですが、 列車がトンネルの中を通過するとき、 観察者Ａにとっては、 列車がすっぽりとトンネルの中に入ってしまう瞬間があるのです。 常識的なニュートン力学ではありえないことが、 真実的な相対性理論ではありえるのです。 そこで、 これは 「 トンネルと列車のパラドックス 」 と名付けられました。 パラドックスとは、 一見偽に思えるけれども熟考すると真の命題のことを言います。

トンネルの入り口と列車の後端がちょうど重なる瞬間を、 観察者Ａにとっても観察者Ｂにとっても時刻 とします。 この２人にとって、 時刻 に、 列車の先端がトンネル内にあるかどうかを調べてみましょう。 「 そんなの簡単だ。 観察者Ａにとっては、 ローレンツ収縮によって、 列車の先端はトンネル内にあるが、 観察者Ｂにとっては、 列車の先端はトンネル外にある。」 と言っている人がいますが、 そのとおりです。 そこで、 これをグラフを用いて見てみることにしましょう。

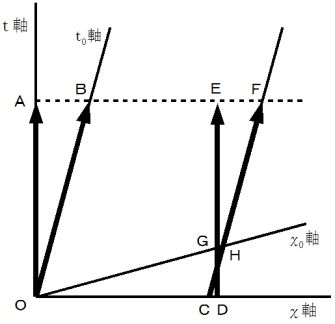
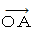　　 ：　トンネルの入口の時空間移動　　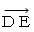　　　 ：　トンネルの出口の時空間移動

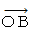　　 ：　列車の後端の時空間移動　　　　　　　 ：　列車の先端の時空間移動

　　直交座標系における 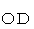の長さ ：　トンネルの固有長 ＝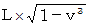

　　斜交座標系における の長さ ：　列車の固有長 ＝

　　

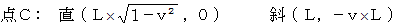
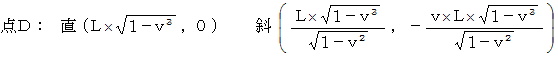
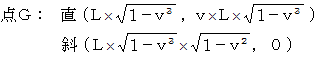
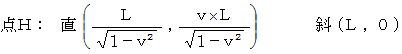
　　観察者Ａの、 時刻 における第３者的な主観的な観察の結果より、

　　　　　　　列車の長さ 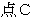：　 の直交座標系における 座標値　＝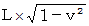

　　　　　　　トンネルの長さ ：　 の直交座標系における 座標値　＝

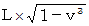
　　　　　　　 より、 列車はトンネルの中に完全に入っています。


　 そういうわけで、 「 トンネルと列車のパラドックス 」 が成り立っていることがわかりました。

しかし、 ここで、 次のような疑問が湧いてきます。

「 『 トンネルと列車のパラドックス 』 が立っている土台が矛盾しているので、 『 トンネルと列車のパラドックス 』 自体が矛盾ではないか？ 」

その根拠は、 次の事実によります。

　 まず、 観察者Ｂの第３者的な主観的観察では、 明らかに、 列車は常にトンネルからはみ出ています。 次に、 観察者Ａの、 観察者Ｂについての、 当事者的な客観的な観察でも、 列車は常にトンネルからはみ出ています。 なぜなら、 次のようになっているからです。

　　　列車の長さ ：　 の斜交座標系における 座標値　＝

　　　トンネルの長さ 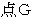：　 の斜交座標系における 座標値　＝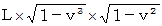

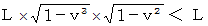　　　 より、 列車はトンネルからはみ出ています。

観察者によって、 トンネル内に列車がすっぽりと入る瞬間が有るか無いかが異なるのは、 おかしなことです。 したがって、 「 トンネルと列車のパラドックス 」 自体が矛盾であり、 それを導きだす 「 ローレンツ変換は、 相対論的な４次元時空間のベクトルの座標変換である。」 という命題が正しいのだろうかという疑問が湧いてきます。