ガリレイ変換	ローレンツ変換

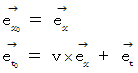
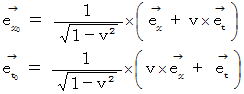
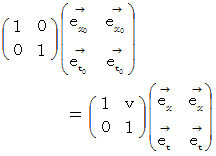
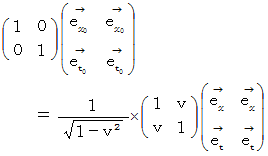
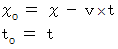
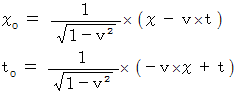
　 まず、 座標変換による基底の大きさの変化に注目してください。 ガリレイ変換では、 空間の基底の要素は 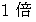、 時間の基底の要素は 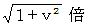になっており、 ローレンツ変換では、 空間の基底の要素 も 時間の基底の要素も 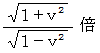になっています。 ガリレイ変換では、 座標変換前に時間成分が０のベクトルは、 座標変換後の空間成分 が座標変換前と同じになっており、 座標変換後に空間成分が０のベクトルは、 座標変換後の時間成分が 座標変換前と同じになっています。 これは、 「 ガリレイ変換では、 空間や距離の物差しの単位目盛りの長さは、 座標変換にて不変である。」 ということを示しています。 ということは、 「 ガリレイ変換は、 空間や時間の大きさを変えない座標変換である。」 ということです。

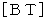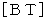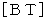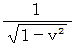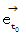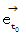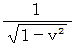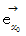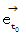　 次に、 ガリレイ変換とローレンツ変換の 「 基底変換テンソル 」 の違いに注目してください。 ローレンツ変換の の表現行列は、 ガリレイ変換の の表現行列の２行目＆１列目の成分が から に置き換わって、 全体の成分が 倍 になっています。 また、 ローレンツ変換後の は、 ガリレイ変換後の と比べて、 方向は同じで、 大きさが 倍 になっています。 また、 ローレンツ変換では、 と が 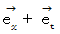に対して対称になっています。

　 ということは、 「ローレンツ変換は、 ガリレイ変換を、 空間軸の基底についても、 時間軸の基底と同様の基底変換をするようにして、 その後にすべての基底の要素の大きさを 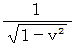倍 にしたものであり、 空間と時間が平等に取り扱われる座標変換である。」 ということです。

では、 基底の大きさが 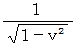倍 になっているルーツは何でしょうか？　マイケルソン ・ モーレーの実験からすると、 それは垂直方向と水平方向の光の速さの違いに由来しそうです。 （ これは、 ローレンツ収縮に由来すると言ってもよいと思います。）　しかし、 ローレンツ変換の起源は 「 マックスウェル方程式の相対性原理 」 ですから、 ローレンツ収縮とは無縁であると考えるべきではないでしょうか。