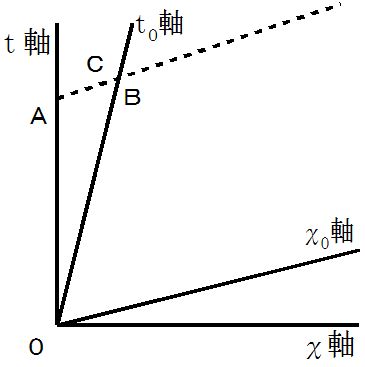
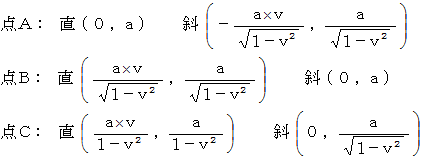
このとき、 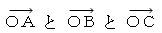は、 それぞれ次のように表されます。

　 ローレンツ変換 や 逆ローレンツ変換は、 同一物質の時空間移動についての座標変換です。 したがって、 ローレンツ変換 や 逆ローレンツ変換は、 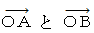との対応 や 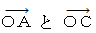との対応 のことではなくて、 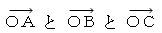それぞれについての、 直交座標表示 と 斜交座標表示との対応です。 ローレンツ変換や逆ローレンツ変換で特に注目すべきは、 この３つのベクトルのうち 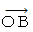です。 なぜなら、 固有時間が だからです。

空間座標値の２乗 と 時間座標値の２乗 との差は、 斜交座標表示と直交座標表示で等しくなっています。 しかし、 空間座標値の２乗 と 時間座標値の２乗 との和は、 斜交座標表示のほうが直交座標表示に比べて必ずしも 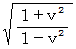倍大きくなっているわけではありません。

　 ローレンツ変換 や 逆ローレンツ変換は、 時空原点を共有する２人の観察者の、 空間を一定の速度で移動している１つの物質に対する観察内容を比較したものではありません。 ローレンツ変換 や 逆ローレンツ変換は、 １人の観察者の、 空間を一定の速度で移動している１つの物質に対する 「 第３者的な主観的観察 （ ニュートン力学的観察 ）」　と　「 当事者時な客観的観察 （ 相対論的観察 ）」　とを比較したものです。 この 「 第３者的な主観的観察 （ ニュートン力学的観察 ）」　と　「 当事者時な客観的観察 （ 相対論的観察 ）」　との比較では、 時空原点を通過する物質については、 ニュートン力学では存在しない時刻のズレが生じ、 また、 時空原点を通過しない物質については、 その上に、 「 第３者的な主観的観察 （ ニュートン力学的観察 ）」　の　「 基本的な第３者的な主観的観察 （ 純粋なニュートン力学的観察 ） 」　と　「 応用的な第３者的な主観的観察 （ 矯正されたニュートン力学的観察 ）」　への分裂が生じます。