（12） ガリレイ変換とローレンツ収縮でローレンツ変換を作る

ローレンツ変換
　　　　
　　　　

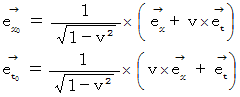
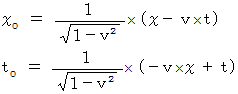
ガリレイ変換
　　　　
　　　　

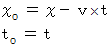
ローレンツ収縮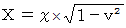
　　　　


　 まず、 時間座標について見ていきます。
　 ガリレイ変換後の 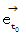は、 ローレンツ変換後 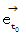と比べて、 方向は同じで、 大きさが 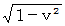倍 小さくなっています。 しかし、 そこにローレンツ収縮を加えると、 空間が 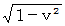倍 に小さくなって時間の短さが打ち消されるために、 ローレンツ変換と同様の変換に換えることができます。


　 次に、 空間座標について見ていきます。
　 ガリレイ変換 と ローレンツ収縮 の式より、 次の式が成り立ちます。
　　　　　
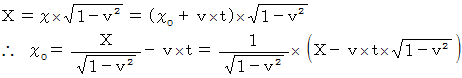
この式に、 「 固有時間不変 」 の相対性理論から導かれる次の式を代入します。
　　　　　
すると、 上記の式は、 次のようになります。
　　　　　
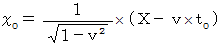
ガリレイ変換より、 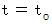ですので、 この式は次のようになります。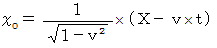
　　　　　
これは、 ローレンツ変換の空間座標値の変換式に似ています。


　 そういうわけで、 なんだか怪しい操作で、 ガリレイ変換 と ローレンツ収縮 からローレンツ変換の類似品を作ることができました。 なお、 本当のローレンツ変換は、 ニュートン力学的観察 を 相対論的観察 に翻訳するための道具であり、 ガリレイ変換とローレンツ収縮を組み合わせた翻訳グッズよりも、 すぐれ物です。