ばいおりんの慣性系相対性理論

（３）物質の姿についての座標変換

　　

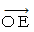　　：　第１観察者に対して速さ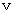で移動している物質の後端の軌跡
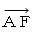　　：　第１観察者に対して速さ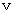で移動している物質の先端の軌跡

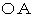　　：　第１観察者の第３者的な主観的観察による、物質の長さ

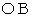　　：　第１観察者の当事者的な客観的観察による、第０観察者（この物質たちと

並走している観察者）にとっての、物質の長さ

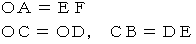
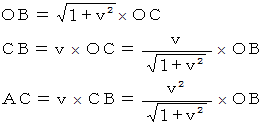
これから、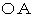と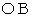の関係を求めてみましょう。

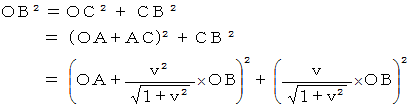
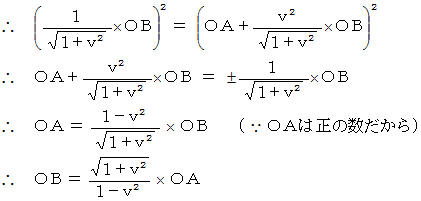
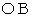　ここで、斜交座標系の基底は、直交座標系の基底のですから、を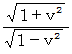で割ったものが、実際の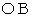の長さになります。

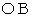　したがって、の長さは、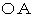を用いて次のように表されることがわかります。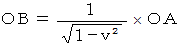
　

　以上の方法は、まどろっこしい方法でした。本当は、点Ａの斜交座標系のχ座標値と直線座標系のχ座標値とを比較すべきなのですが。とまれこうまれ、定説は「ローレンツ変換によって空間は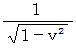倍に伸展するので、第０観察者から第１観察者への座標変換では、空間が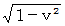倍に収縮する。」と言うことになります。しかし、これはあくまで、「間違っているニュートン力学的観察（第３者的な主観的観察）」と「正しい相対論的観察（当事者的な客観的観察）」とを比較しただけのことですから、実際に２つの座標系で空間の体積が異なっているわけではないと、私は考えています。

　　

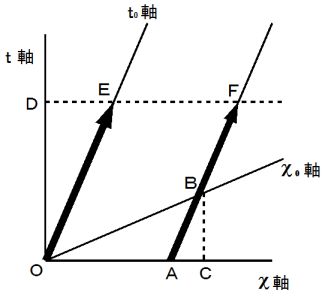
　これは、先ほど示した図です。今度は、図の時空点に具体的な座標値を与えて、定説の「 ローレンツ収縮 」の説明をしてみましょう。
次のようにします。
　　　　　

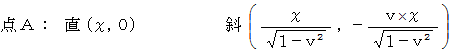
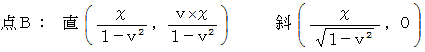
　の直交座標系の空間座標値は、斜交座標系の空間座標値よりも倍小さいことに注目してください。この事実だけで、移動している物質における「ローレンツ収縮」の説明になっているのですが、なにかピンボケしています。なぜなら、斜交座標系では物質の両端を同時に測定していないからです。（本当は、斜交座標系では物質は静止していますので、両端を同時に測定していなくてもきちんと物質の長さを計れているのですが。）
　そこで、定説は次のように説明します。
　このとき、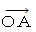と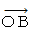の斜交座標系の空間座標値は等しくなっています。したがって、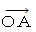の直交座標系の空間座標値は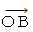の斜交座標系の空間座標値よりも倍小さくなっています。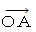の直交座標系の空間座標値は、第３者的な主観的観察による移動している物質の長さを表し、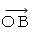の斜交座標系の空間座標値は、当事者的な客観的観察によるその物質の固有長を表しています。こうして、「ローレンツ収縮」はストンと私たちの腹の中に納まります。