（６） ４次元時空間距離を不変にする座標変換

　 ニュートン力学におけるガリレイ変換は、 座標変換の前後で 「 時間 」 を不変にする変換ですが、 これは直交座標系から直交座標系への座標変換なのでしょうか？　いいえ、 違います。 ガリレイ変換は、 次のような、 直交座標系から斜交座標系への座標変換です。

　　　　　
　　　　　
　　　　　
　　　　　

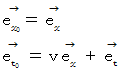
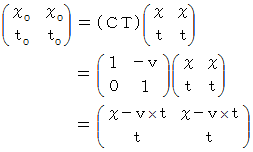
　 ローレンツ変換は、 時間を虚数としたときに、 ４次元時空間距離を不変にする座標変換です。 このことは、 「 固有時間 」 を用いて、 次のように表されます。
　　　　　
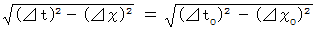
　 では、 ニュートン力学におけるガリレイ変換は、 時間を実数としたときに、 次のように、 ４次元時空間距離を不変にする座標変換なのでしょうか？
　　　　　
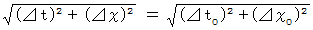
答えは、 いいえ です。 その理由は、 次の式を見ればわかります。
　　　　　
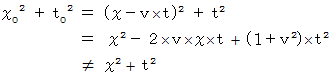
ガリレイ変換は、 時間を実数としたときに、 次のように、 時間を不変にする座標変換です。
　　　　　

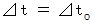
　 では、 時間を実数としたときに、 次のように４次元時空間距離を不変にする座標変換は、 どんな座標変換でしょうか？
　　　　　
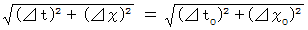
それは、 次のような、 直交座標系から直交座標系への座標変換です。

　　　　　

　　　　　
　　　　　
　　　　　
　　　　　
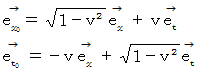
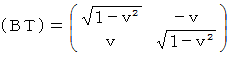
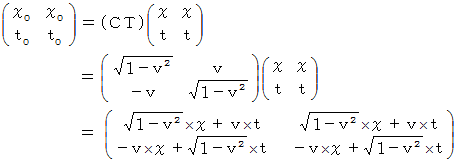
では、 確かめてみましょう。
　　　　

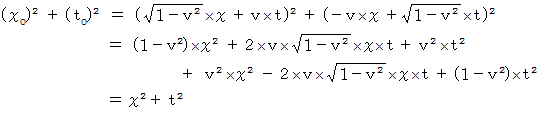
　 この座標変換は、 ベクトルを 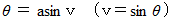　だけ時計回りに回転する写像と同じです。