（７） ベクトルの座標変換で考える同時刻の相対性

　 田舎の駅を特急電車が通過します。 電車の真ん中に乗客がおり、 電車の前後に光源があります。 乗客がプラットホームの普通電車を待っている人とすれ違った瞬間に、 前後の光源が閃光を放ちます。 閃光は、 乗客や待ち人に届きます。


　基本的なニュートン力学的観察

　図−１

　　　　　
　　　　　
　　　　　
　　　　　
　　　　　


　　　　

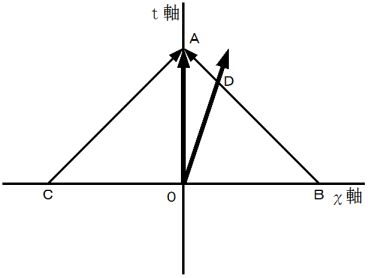
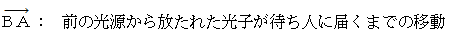
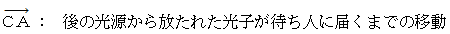
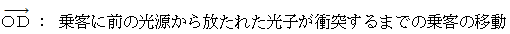
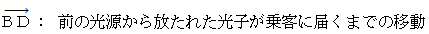
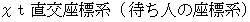
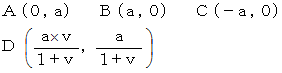
待ち人の当事者的な主観的観察による、 待ち人が光子と衝突するまでの時間 ：
　　　　　　
待ち人の第３者的な主観的観察による、 乗客が光子と衝突するまでの時間 ：
　　　　　　

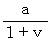
図−１ には、 「 待ち人による、 自分についての、 当事者的な主観的観察 （ 待ち人の当事者的な主観的観察 ）」 と 「 待ち人による、 乗客についての、 第３者的な主観的観察 （ 基本的第３者的ニュートン力学的観察 ）」 が描かれています。 図−１ は、 私たちにとってきわめて常識的な図です。 そして、 この図が示す 「 待ち人による、 乗客についての、 第３者的な主観的観察 （ 基本的第３者的ニュートン力学的観察 ）」 をスタート点にして、 ローレンツ変換を行いますと、 混乱に陥ります。 その混乱は次ののようなものです。


　間違ったローレンツ変換の使用法

　図−２



　　　　

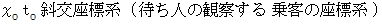
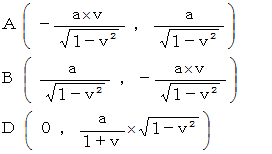
待ち人が光子と衝突するまでの時間 ：
　　　　　　
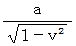
乗客が光子と衝突するまでの時間 ：
　　　　　　


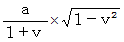
　 相対性理論の考え方では、 移動している慣性系は、 移動方向に収縮し、 ゆっくりと時が経過しています。 したがって、 待ち人が、 乗客について当事者的な客観的観察をすると、 移動している慣性系の中で静止している乗客に衝突する光子の移動距離は、 待ち人にとっての よりも長くて、 かつ、 光速は ですから、 光子が乗客に衝突するには よりも多くの時間がかかりそうに思われますが、 移動している慣性系の時の経過は遅くなっていますので、 それらが相殺されて、 結局、 待ち人が光子と衝突するまでの時間 と 乗客が光子と衝突するまでの時間 は等しくなっていいます。 これは別の言い方をすれば、 「 静止していると見なされる待ち人の固有時間 と 静止していると見なされる乗客の固有時間は等しい。」 ということになります。 しかし、 このことが 図−２ では実現されていません。


　逆ローレンツ変換

待ち人による、 乗客についての、 当事者的な客観的観察 （ 斜交座標系 ）
　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　待ち人による、 乗客についての、 第３者的な主観的観察 （ 直交座標系 ）
　　　　　　　　　　　　　（ 応用的第３者的ニュートン力学的観察 ）


　図−３

　　　　
　　　　
　　　　


　　　　


　　　　


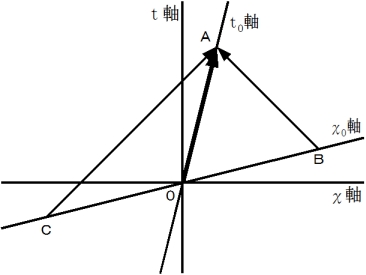
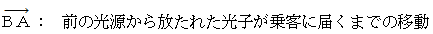
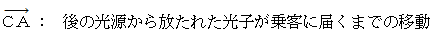
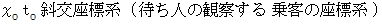
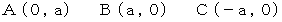
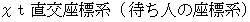
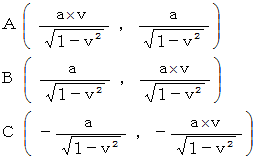
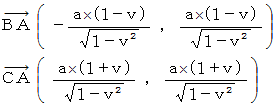
　ローレンツ変換 ：

待ち人による、 乗客についての、 第３者的な主観的観察 （ 直交座標系 ）
　　　　　　　　　　　　　（ 応用的第３者的ニュートン力学的観察 ）
　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　待ち人による、 乗客についての、 当事者的な客観的観察 （ 斜交座標系 ）


　図−４　（ 図−３ と同じです。）



　　　　


　　　　

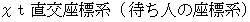
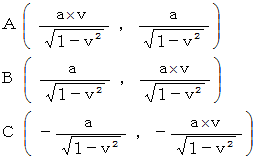
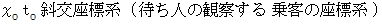
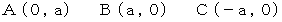
待ち人の第３者的な主観的観察による、 乗客が光子と衝突するまでの時間
　　　　　
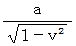
待ち人の乗客に関する当事者的な客観的観察による、 乗客が光子と衝突するまでの時間
　　　　　


の手順、 つまり、 まず、 「 待ち人による、 乗客についての、 当事者的な客観的観察 」 をスタート点にして、 ローレンツ逆変換から開始して、 その逆変換のローレンツ変換にたどりつけば、 一応、 整合性のあるものになります。 なぜならば、 「 座標変換で固有時間は不変である。」 という相対性理論の定理が守られているからです。 つまり、 「 待ち人の当事者的な主観的観察による、 固有時間 （ 図−１ の 点Ａ の直交座標系の時間座標値 ）」 と 「 待ち人による、 乗客についての、 当事者的な客観的観察による、 固有時間 （ 図−４ の 点Ａ の斜交座標系の時間座標値 ）」 が等しくなっているからです。

　 そういうわけで、 結局、 次のような結果にまとめることができます。

　　　ａ）　待ち人の第３者的な主観的観察による、 乗客が光子と衝突するまでの時間
　　　　　　　　
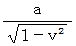
　　　ｂ）　待ち人の当事者的な客観的観察による、 乗客が光子と衝突するまでの時間
　　　　　　　　
　　　ｃ）　待ち人の当事者的な主観的観察による、 待ち人が光子と衝突するまでの時間
　　　　　　　　

　 ａ） ｂ）　は、 ニュートン力学的観察 から 相対論的観察 への翻訳です。 つまり、 ローレンツ変換です。 また、　ｂ） ＝ ｃ）　は、 「 座標変換によって固有時間は不変である。」 ことに由来します。 つまり、 自分の座標系 （ その中では観察者は静止しています ） の時間は固有時間であり、 「 当事者的な観察 」 による時間も、 観察の対象となる人を静止していると見なしているので、 固有時間であるということです。


　 さて、 図−１ の中の 「 待ち人の当事者的な主観的観察 （ 直交座標系 ）」 と 図−４ の中の 「 待ち人による、 乗客についての、 第３者的な主観的観察 （ 応用的第３者的ニュートン力学的観察 ） （ 直交座標系 ）」 とを重ねてみましょう。 すると、 次のようになって、 違和感を覚えます。

　図−５

　　　　　　
　　　　　　


　　　　
　　　　
　　　　
　　　　

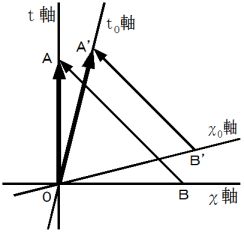
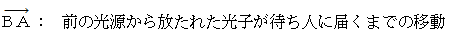
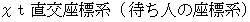
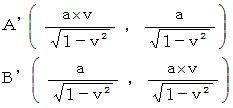
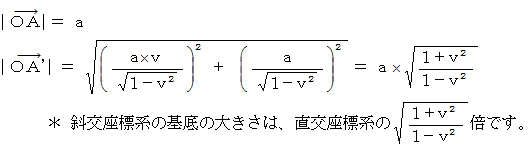
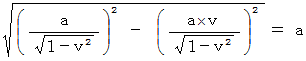
以上のように、 「 待ち人の当事者的な主観的観察 」 と 「 待ち人による、 乗客についての、 第３者的な主観的観察 （ 応用的第３者的ニュートン力学的観察 ）」 とでは、 同時刻に同空刻で発射されたはずの２つの光子たち （ 待ち人に衝突する光子 と 乗客に衝突する光子 ） が、 発射される時刻も空刻も異なるし、 したがって移動する時空間も異なっています。 これは、 「 座標変換による時空刻の相違性 」 や 「 同時刻性の相対性 」 とは違い、 どう見ても整合性はありません。
　 したがって、 「 基本的第３者的ニュートン力学的観察 」 にしろ 「 応用的第３者的ニュートン力学的観察 」 にしろ、 「 第３者的なニュートン力学的観察 」 は、 錯覚的なものであり、 当事者的な客観的観察をしなければならないことがわかります。



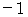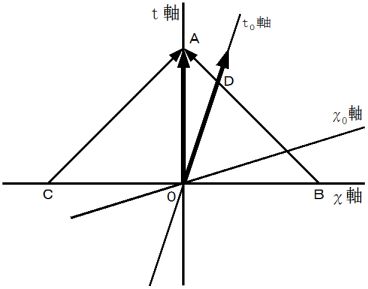
　 最後に、 観察者と時空原点を共有して様々な速度で空間移動している無数の物質 （ 人や量子も含む ） に注目してみましょう。 時空原点を同時に出発し、 １次元空間を から の間の任意の速さで等速直線運動をする無数の物質を観察している第１観察者がいます。 彼は、 それぞれの物質と並走している無数の第０観察者たち１人１人について、 当事者的な客観的観察をします。無数の第０観察者たちの固有時間が共通に 経過する間 の物質の時空間移動を斜交座標系の黒線で表すと、 次の３つの線で囲まれた部分が黒色で塗りつぶされることになります。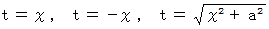
　　　　


次のページへ進む　　　 論文の最初へ戻る　　　 前のページへ戻る