ばいおりんの慣性系相対性理論

（８）特殊相対性理論の守備範囲

　完全弾性衝突により一瞬にして速度を変える点状物質の移動は別にして、一般的には、速度が変わる物質の移動については、特殊相対性理論の守備範囲ではありません。ただし、「双子のパラドックス」は、一瞬にして同じ速さでＵターンする点上物質の移動であるというシチュエーションにすれば、特殊相対性理論の守備範囲になりますので、特殊相対性理論は「双子のパラドックス」について、きちんと責任を果たさなければなりません。しかし、「 急発進する棒のパラドックス 」について、特殊相対性理論に責任を押し付けるのは間違いです。
　「急発進する棒のパラドックス」とは、「一瞬にして等速直線運動を開始した後の棒と同じ速度で移動している観察者にとっては、棒の両端が急停止する時刻に差があるために、その間に棒が伸展する。これは変ではありませんか？」というものです。
　簡略化のため空間を１次元とします。棒の両端をＮ端とＳ端とし、Ａさんの座標系において、Ｎ端が時空原点に静止しているとします。Ｂさんが、Ｎ端の側から速さ

で棒に近づいてきています。ＢさんがＮ端に接触する瞬間を、２人にとって時刻

とします。そして、時刻

に、その棒が突然にＢさんと同じ速度で移動し始めたとします。２人の観察者にとっての棒の時空間移動は、次のようになります。斜交座標系は、Ａさんの当事者的な客観的観察による、Ｂさんの慣性系の世界です。

　直交座標系：
　　　　　

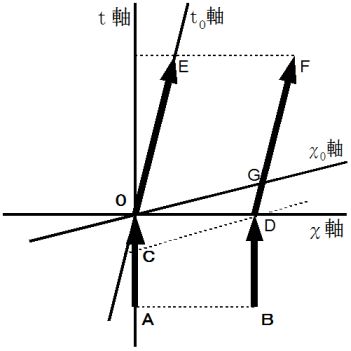
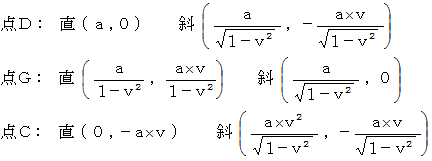
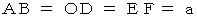
　斜交座標系：
　　　　　

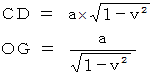
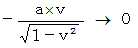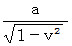　この図によると、Ａさんの当事者的な客観的観察によるＢさんの慣性系の世界では、時刻がと経過する間、棒のＳ端は静止していて、棒のＮ端はＳ端と反対方向に移動しますので、この間に、棒の長さはと次第に伸展していくことになります。これは、おかしなことです。また、時刻までの棒の固有長はであり、その期間中は、Ｂさんにとっては棒の長さはにローレンツ収縮しており、時刻以後の棒の固有長はであり、その期間中は、Ａさんにとっては棒の長さはにローレンツ収縮しています。棒の固有長が突然に変化しており、これも、おかしなことです。

　そういうわけで、特殊相対性理論の守備範囲を超えたものを、特殊相対性理論で説明しようとすると、特殊相対性理論の矛盾の中に一層深く入り込んでしまうことになります。