第6章 等価原理
(1) 重力のある風景
-
重力場の中にリンゴと観察者が存在します。 リンゴの移動とは、 リンゴ と 観察者 との運動関係です。 その運動関係にはいろんなスタイルがあります。
これから、 それぞれのスタイルに似たような状況を、 無重力空間の中で作ってみましょう。
 ロケットエンジンを付けた観察者がエンジンを噴射して、 宙に浮いた状態で静止しており、 リンゴが地面に向かって落下しているのを観察している場面 を作ろう。
ロケットエンジンを付けた観察者がエンジンを噴射して、 宙に浮いた状態で静止しており、 リンゴが地面に向かって落下しているのを観察している場面 を作ろう。観察者とリンゴが漂っています。 観察者に付けたロケットエンジンをかけると、 観察者は加速的変速度運動をします。 すると出来上がります。
( 重力から自由な観察神が観察する、 落下している物質 )
↓↓
( 自力変速度運動をしている観察者が観察する、 無重力状態の物質 )
* 無重力状態の = 等速直線運動( 静止も含む )している
 観察者が渓谷の崖に立っていて、 1個のリンゴは自分に向って、もう1個のリンゴは谷に向かって落下している場面 を作ろう。
観察者が渓谷の崖に立っていて、 1個のリンゴは自分に向って、もう1個のリンゴは谷に向かって落下している場面 を作ろう。等速直線運動しているロケットの中は無重力です。 観察者は、 足をロケットの床に接触させています。 1個のリンゴはロケットの中央でフワフワしており、 また、 もう1個のリンゴはロケットの外にあり、 ロケットと同じ速度で移動しています。 エンジンをかけるとロケットは加速的変速度運動します。 すると出来上がります。
( 重力固定観察者が観察する、 落下している物質 )
↓↓
( 押し上げ変速度運動を被っている観察者が観察する、 無重力状態の物質 )
 観察者が地上に立っていて、 地上にあるリンゴを観察している場面 を作ろう。
観察者が地上に立っていて、 地上にあるリンゴを観察している場面 を作ろう。等速直線運動しているロケットの中は無重力です。 観察者は、足 をロケットの床に接触させています。 りんごもロケットの床に接触しています。 エンジンをかけるとロケットは加速的変速度運動します。 すると出来上がります。
( 重力固定観察者が観察する、 重力固定物質 )
↓↓
( 押し上げ変速度運動を被っている観察者が観察する、 押し上げ変速度運動を被っている物質 )
 観察者が落下しながら、 地上にあるリンゴを観察している場面 を作ろう。
観察者が落下しながら、 地上にあるリンゴを観察している場面 を作ろう。等速直線運動しているロケットの中は無重力です。 観察者は、 ロケットの外にいて、 ロケットと同じ速度で等速直線運動をしています。 リンゴはロケットの中にあり、 床に接触しています。 エンジンをかけるとロケットは加速的変速度運動します。 すると出来上がります。
( 落下中観察者が観察する、 重力固定物質 )
↓↓
( 無重力状態の観察者が観察する、 押し上げ変速度運動を被っている物質 )
 リンゴと一緒に落下している観察者が、 リンゴを観察している場面 を作ろう。
リンゴと一緒に落下している観察者が、 リンゴを観察している場面 を作ろう。観察者とリンゴが漂っています。 もう出来上がっています。
( 落下中観察者が観察する、 落下している物質 )
↓↓
( 無重力状態の観察者が観察する、 無重力状態の物質 )
-
次に、 思い浮かべてください。 無重力空間に6面体の箱があり、 その中に観察者がいて、 両足底を箱の底に接触させています。 箱の高さは 5m で、 幅 と 奥行き は 地球の円周の8倍です。 箱の側面から、 反対側の側面に向けて、 箱の底と平行に、 レーザー光が発せられ、 同じ所から同時に同じ方向に 矢 と 砲丸 が 異なる速さで等速直線運動を開始しました。
これを、 場面0 とします。
場面0 において、 空間に、 大きさが 10 m/s2 、向きが 箱の天井から底に向かう 一様な重力場を作ります。 ただし、 箱には重力を相殺する力を作用させます。 すると、 観察者は、 レーザー光 と 矢 と 砲丸 が 同時に箱の底に接触するのを観察します。 これは、「 質量の等価原理( 慣性質量 = 重力質量 )」と「 光変速度の公理 」によります。
これを、 場面1 とします。
場面0 において、 箱を底から天井の方向に引っ張り、 大きさが常に 10m/s2 の変速度の加速的変速度運動をさせます。 すると、 観察者は、 レーザー光 と 矢 と 砲丸 が 同時に箱の底に接触するのを観察します。
これを、 場面2 とします。
このとき、 場面1 と 場面2 とを区別することができません。
-
次の 1. 〜 3. は同義であり、 このことは「 相対論的等価原理 」と言われます。
一般的に「 等価原理 」と言えば、 このことを示します。
1.「 一様な重力場での変速度 」と「 相対的変速度 」とは区別することができないし、
また、 これらは合成されて、 実際の変速度を得る。
2.「 一様な重力 」と「 相対的変速度力 」とは区別することができないし、 また、
これらは合成されて、 実際の重力を得る。
3.「 一様な重力場 」と「 相対的一様重力場 」とは区別することができないし、
また、 これらは合成されて、 実際の重力場を得る。
「 一様な重力 」と「 相対的変速度力 」との合成の例を、 次にいくつか紹介します。
 一様な重力場( G )の中で、 落下している観察者が、 落下している質量 m の物質を観察している。 その観察者にとっての物質に働いている重力は 0 であり、 その物質は無重力状態である。
一様な重力場( G )の中で、 落下している観察者が、 落下している質量 m の物質を観察している。 その観察者にとっての物質に働いている重力は 0 であり、 その物質は無重力状態である。なぜなら、
物質に働いている既存の重力は G × m である。
物質に働いている相対的変速度力は −G × m である。
この2つを合成して、 0 になる。
 無重力中で、 変速度 a の自力変速度運動をしている観察者が、 等速直線運動( 静止も含める )している質量 m の物質を観察している。 その観察者にとっての物質に働いている重力は m × a であり、 その物質は落下している。
無重力中で、 変速度 a の自力変速度運動をしている観察者が、 等速直線運動( 静止も含める )している質量 m の物質を観察している。 その観察者にとっての物質に働いている重力は m × a であり、 その物質は落下している。なぜなら、
物質に働いている既存の重力は 0 である。
物質に働いている相対的変速度力は m × a である。
この2つを合成して、 m × a になる。
 上記のシチュエーションに、 −a の一様な重力場を加えると、 次のようなシチュエーションになります。
上記のシチュエーションに、 −a の一様な重力場を加えると、 次のようなシチュエーションになります。一様な重力場( a )の中で、 重力から自由の観察神が、 落下している質量 m の物質を観察している。 その観察神にとっての物質に働いている重力は m × a であり、 その物質は落下している。
なぜなら、
物質に働いている既存の重力は m × a である。
物質に働いている相対的変速度力は 0 である。
この2つを合成して、 m × a になる。
 無重力中で、 変速度 a の押し上げ変速度運動を被っている観察者が、 等速直線運動( 静止も含める )している質量 m の物質を観察している。 その観察者にとっての物質に働いている重力は m × a であり、 その物質は落下している。
無重力中で、 変速度 a の押し上げ変速度運動を被っている観察者が、 等速直線運動( 静止も含める )している質量 m の物質を観察している。 その観察者にとっての物質に働いている重力は m × a であり、 その物質は落下している。なぜなら、
物質に働いている既存の重力は 0 である。
物質に働いている相対的変速度力は m × a である。
この2つを合成して、 m × a になる。
 上記のシチュエーションに、 −a の一様な重力場を加えると、 次のようなシチュエーションになります。 なぜなら、 観察者に押し上げ変速度力を作用している箱は変速度運動をやめ等速直線運動をするようになるからです。
上記のシチュエーションに、 −a の一様な重力場を加えると、 次のようなシチュエーションになります。 なぜなら、 観察者に押し上げ変速度力を作用している箱は変速度運動をやめ等速直線運動をするようになるからです。重力場( a )の中で、 重力固定観察者が、 落下している質量 m の物質を観察している。 その観察者にとっての物質に働いている重力は m × a であり、 その物質は落下している。
なぜなら、
物質に働いている既存の重力は m × a である。
物質に働いている相対的変速度力は 0 である。
この2つを合成して、 m × a になる。
 無重力中で、 変速度 a の押し上げ変速度運動を被っている観察者が、 変速度 a の押し上げ変速度運動を被っている質量 m の物質を観察している。 その観察者にとっての物質に働いている重力は m × a であり、 その物質には同時に重力の反作用も働いていて、 その物質は重力固定し静止している。
無重力中で、 変速度 a の押し上げ変速度運動を被っている観察者が、 変速度 a の押し上げ変速度運動を被っている質量 m の物質を観察している。 その観察者にとっての物質に働いている重力は m × a であり、 その物質には同時に重力の反作用も働いていて、 その物質は重力固定し静止している。なぜなら、
物質に働いている既存の重力は 0 である。
物質に働いている相対的変速度力は m × a である。
この2つを合成して、 m × a になる。
この物質には、 この力を相殺する反作用も働いている。
したがって、 この物質には力が働いていないのと同じである。
 上記のシチュエーションに、 −a の一様な重力場を加えると、 次のようなシチュエーションになります。
上記のシチュエーションに、 −a の一様な重力場を加えると、 次のようなシチュエーションになります。一様な重力場( a )の中で、 重力固定観察者が、 重力固定している質量 m の物質を観察している。 その観察者にとっての物質に働いている重力は m × a であり、 その物質には同時に重力の反作用も働いていて、 その物質は重力固定し静止している。
なぜなら、
物質に働いている既存の重力は m × a である。
物質に働いている相対的変速度力は 0 である。
この2つを合成して、 m × a になる。
この物質には、 この力を相殺する反作用も働いている。
したがって、 この物質には力が働いていないのと同じである。
これらは、 結局、 次のことと同義であり、 重力で考えるよりも重力場で考えたほうがわかりやすいように思います。
「 変速度の大きさが a の変速度運動をしている観察者の座標系には、 全空間に一様な重力場( −a )が生じており、 この 『 相対的一様重力場 』 を既存の重力場と合成すれば、 観察者の座標系での実際の重力場になっている。」
第7章 重力場による時間経過遅延作用
GPS衛星内の原子時計は地上の原子時計よりも速く時を刻むそうですが、 いったいどれくらい進むのでしょうか?
「 重力場による時間経過遅延 」を導くためには、 まず、「 重力場による空点時間の収縮 」を導きます。 そして、「 空点時間は絶対的なものであるから、 その長さの違いは、 時間の経過するスピードの違いを表す。」と宣言した後、「 空点時間は相対的なものであるから、 重力場の位置エネルギーが相対的に高い空点に存在する観察者からは、 重力場の位置エネルギーが相対的に低い空点に存在する心臓の1回拍動時間が間伸びして観察されるので、 重力場によって時間の経過が遅延する。」と言い切ります。
「 重力場による空点時間の収縮 」を求めるためには、 まず、 重力場によって作られる落下物質の空間移動速度を、 特殊相対性理論の「 速さ
 で等速直線運動している物質の相対時間は
で等速直線運動している物質の相対時間は 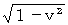 倍だけ絶対時間よりも短かい。」という式に代入して相対時間を求め、 次に、 その相対時間 を 空点時間 に置き換えます。
倍だけ絶対時間よりも短かい。」という式に代入して相対時間を求め、 次に、 その相対時間 を 空点時間 に置き換えます。* 「 空点時間 」は私の造語です。 重力場の影響で経過速度が遅延した絶対
時間を表しています。
「 重力場による時間経過遅延 」を導くには、 これ以外に、 光の伝わる道のりの違いから求めようとする試みがあります。
(1)重力ポテンシャルによる時間経過遅延
-
GPS衛星内の時計の時間補正には、 速度による時間経過遅延に対する補正 と 重力ポテンシャルによる時間経過遅延に対する補正 があるそうです。 補正値の絶対値は、 後者のほうが大きいそうです。 GPS衛星の軌道の空点たちは、 地上の空点よりも重力ポテンシャルが低いので、 実際には、 GPS衛星内時計の重力ポテンシャル差による時間経過遅延の補正については、 クイックに対する補正が必要になります。
* 重力ポテンシャル: 地球の質量を
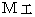 とし、
とし、ある空点の地球の重心からの距離を
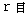 とすると、
とすると、その空点の重力ポテンシャルは次の式で表されます。
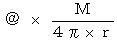 ( @は重力定数 )
( @は重力定数 )GPS衛星の軌道半径を
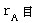 とします。
とします。地球の半径を
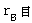 とします。
とします。地球の質量を
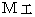 とします。
とします。GPS衛星軌道上で地球に対して静止している質量
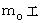 の物質Aを、 地球の引力にまかせて落下させます。 空気抵抗はないものとし、 物質が地面に衝突するときの速さを
の物質Aを、 地球の引力にまかせて落下させます。 空気抵抗はないものとし、 物質が地面に衝突するときの速さを  とします。
とします。GPS衛星軌道上で地球に対して静止している物質Bが微小絶対時間
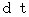 経過する間に、 速さ
経過する間に、 速さ  で地面に衝突している物質Aの移動する微小相対時間の大きさを
で地面に衝突している物質Aの移動する微小相対時間の大きさを 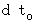 とすると、
とすると、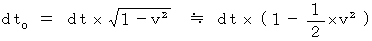 ・ ・ ・ ・(式0701)
・ ・ ・ ・(式0701)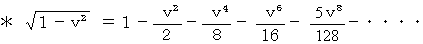
力学的エネルギー保存の法則より、 運動エネルギーの増加量 = 位置的エネルギーの減少量 です。
よって、 運動エネルギーの増加量 + 位置的エネルギーの増加量 = 0 です。 したがって、
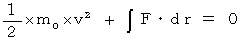 ・ ・ ・ ・(式0702)
・ ・ ・ ・(式0702)位置エネルギーの増加量は次の式で表されます。
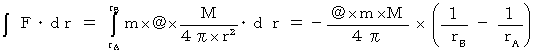
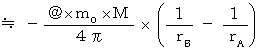 ・ ・ ・(式0703)
・ ・ ・(式0703)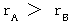 より、(式0703)は負の数になります。
より、(式0703)は負の数になります。(式0703)を(式0702)に代入して、
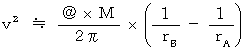 ・ ・ ・ ・(式0704)
・ ・ ・ ・(式0704)(式0704)を(式0701)に代入して、
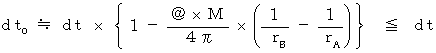
ここで、 相対時間を空点時間に置き換えます。 GPS衛星軌道上の物質Aは、 地球に対して静止していますので、 物質Aの相対時間は絶対時間に等しいです。 こうして、 空点時間GPS衛星軌道上の空点時間に比べて、 地上の空点時間は短くなっていることがわかります。
そこで、次のように考えます。
「 GPS軌道上の空点の観察者からすると、 地上の空点の時間はゆっくりと経過する。 つまり、 重力ポテンシャルの高い空点では、 重力ポテンシャルの低い空点に比べて、 時間はゆっくりと経過する。 ということは、 地上にいる観察者にとっては、 その逆であり、 GPS衛星内の時計は進む。 そこで、 GPS衛星の速さによる時計の遅れを無視するのであれば、 GPS衛星には、
 の時間に必ず次の時間だけ遅れる時計を搭載すれば、 正確な地上の時刻を測定してくれることになる。
の時間に必ず次の時間だけ遅れる時計を搭載すれば、 正確な地上の時刻を測定してくれることになる。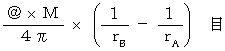 」
」-
大きさが
 の一様な重力場が存在する空間で、 静止している質量
の一様な重力場が存在する空間で、 静止している質量 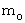 の物質Aが、 重力の作用で加速的変速度運動を開始し、
の物質Aが、 重力の作用で加速的変速度運動を開始し、 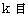 の空間を移動しました。 この瞬間の物質Aの速さを
の空間を移動しました。 この瞬間の物質Aの速さを  とします。 この時、 静止している物質の絶対時間が
とします。 この時、 静止している物質の絶対時間が 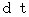 経過するときの、 物質Aの相対時間を
経過するときの、 物質Aの相対時間を 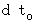 とします。 すると次のようになります。
とします。 すると次のようになります。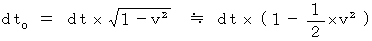 ・ ・ ・ ・(式0701)
・ ・ ・ ・(式0701)力学的エネルギー保存の法則より、 運動エネルギーの増加量 = 位置的エネルギーの減少量 ですから、
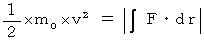 ・ ・ ・ ・(式0702’)
・ ・ ・ ・(式0702’)位置的エネルギーの減少量は、 次の式から求めることができます。
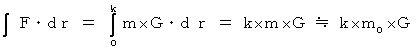 ・ ・ ・ ・(式0705)
・ ・ ・ ・(式0705)(式0705)を(式0702’)に代入して、
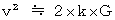 ・ ・ ・ ・(式0706)
・ ・ ・ ・(式0706)(式0706)は(式0702’)を用いなくても求めることができます。
 の一様な重力場が存在する空間では、 重力によりすべての物質は
の一様な重力場が存在する空間では、 重力によりすべての物質は  の大きさの加速度の変速度運動をします。 これを順に時間で積分することによって、
の大きさの加速度の変速度運動をします。 これを順に時間で積分することによって、  の時点での 物質の速さ
の時点での 物質の速さ  と 移動距離
と 移動距離  がわかります。
がわかります。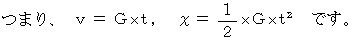
この2つの式から、
 と
と  の関係を求めて、 それに
の関係を求めて、 それに 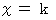 を代入すると、(式0706)を求めることができます。
を代入すると、(式0706)を求めることができます。(式0706)を(式0701)に代入して、
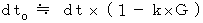 ・ ・ ・ ・(式0707)
・ ・ ・ ・(式0707)以上より、速さ
 で落下している物質Aの相対時間は、 上式で表される割合だけ、 静止していたときの物質Aの 相対時間 = 絶対時間 よりも短くなっていることがわかります。 したがって、 大きさが
で落下している物質Aの相対時間は、 上式で表される割合だけ、 静止していたときの物質Aの 相対時間 = 絶対時間 よりも短くなっていることがわかります。 したがって、 大きさが  の一様な重力場が存在する空間では、 重力場の方向に
の一様な重力場が存在する空間では、 重力場の方向に 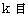 下ると、 時間の経過が
下ると、 時間の経過が  あたり
あたり 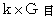 遅れることになります。
遅れることになります。-
大きさが
 の一様な重力場が存在する空間で、 自由落下している、 幅が
の一様な重力場が存在する空間で、 自由落下している、 幅が  のエレベーターの中で、 レーザー光が一方の壁から反対側の壁に向かって水平方向に放たれた場合を考えます。 これを、 エレベーターの中にいてエレベーターと共に落下している観察者Aが観察した場合と、 地上で静止している観察者Bが観察した場合とで比較します。
のエレベーターの中で、 レーザー光が一方の壁から反対側の壁に向かって水平方向に放たれた場合を考えます。 これを、 エレベーターの中にいてエレベーターと共に落下している観察者Aが観察した場合と、 地上で静止している観察者Bが観察した場合とで比較します。観察者Bの観察では、 レーザー光の速さは 1 を超え、 レーザー光の軌跡は次の式で表されます。
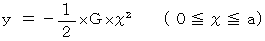
* 媒介変数表示では、
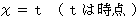
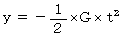
レーザー光が反対側の壁に到達するまでの時間
 に伝わるレーザー光の道のり( 弧長 )は、 次の式から求めることができます。
に伝わるレーザー光の道のり( 弧長 )は、 次の式から求めることができます。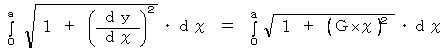
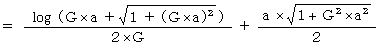
この値を
 とします。
とします。  です。
です。ここで、「 光の速さは 1 なので、 光は、 道のり
 を
を 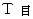 の時間で伝わる。」とします。 よって、 観察者Aの、 重力場の存在しない座標系の時間の経過のスピードに比べて、 観察者Bの、 大きさが
の時間で伝わる。」とします。 よって、 観察者Aの、 重力場の存在しない座標系の時間の経過のスピードに比べて、 観察者Bの、 大きさが  の一様な重力場が存在する座標系の時間の経過のスピードは、
の一様な重力場が存在する座標系の時間の経過のスピードは、 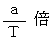 遅くなっているとします。
遅くなっているとします。-
大きさが
 の一様な重力場が存在する空間で、 自由落下している、 幅が
の一様な重力場が存在する空間で、 自由落下している、 幅が  のエレベーターの中で、 レーザー光が一方の壁から反対側の壁に向かって水平方向に放たれた場合を考えます。 これを、 エレベーターの中にいてエレベーターと共に落下している観察者Aが観察した場合と、 地上で静止している観察者Bが観察した場合とで比較します。
のエレベーターの中で、 レーザー光が一方の壁から反対側の壁に向かって水平方向に放たれた場合を考えます。 これを、 エレベーターの中にいてエレベーターと共に落下している観察者Aが観察した場合と、 地上で静止している観察者Bが観察した場合とで比較します。観察者Bの観察では、 レーザー光の速さは、 時間
 の関数で表されます。
の関数で表されます。垂直方向には、
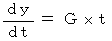
水平方向には、
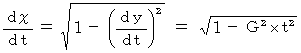
レーザー光の道のり( 軌跡の弧長 )は、 次の式で与えられます。
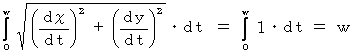
* ただし、
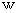 は、 次の条件を満たす値である。
は、 次の条件を満たす値である。レーザー光が放たれてから
 後のレーザー光の水平方向の位置 x :
後のレーザー光の水平方向の位置 x :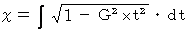
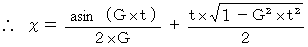
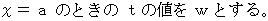
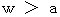 ですので、 観察者Aの、 重力場の存在しない座標系の時間の経過のスピードに比べて、 観察者Bの、 大きさが
ですので、 観察者Aの、 重力場の存在しない座標系の時間の経過のスピードに比べて、 観察者Bの、 大きさが  の一様な重力場が存在する座標系の時間の経過のスピードは、
の一様な重力場が存在する座標系の時間の経過のスピードは、 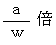 遅くなっているとします。
遅くなっているとします。これらの( 別解答 )たち と 既述の( 定説解答 )では、 答えが一致しません。 なぜなのでしょうか? 徒労に終わるのでしょうか? 現在、 私は考え中です。