Chapter 11 Two Paradoxes about Time Dilation and Length Contraction
Two Paradoxes about Time Dilation and Length Contraction
In this chapter, we challenge the common sense of the theory of relativity. The common sense of the theory of relativity is as follows:

 .
.

Note :
It is clear that
 is wrong. But we tend to have the illusion that
is wrong. But we tend to have the illusion that  is right.
is right.  did not only replace 'he' of
did not only replace 'he' of  by 'we'. If we change
by 'we'. If we change  from his standpoint to our standpoint, we change it as follows :
from his standpoint to our standpoint, we change it as follows : If we travel at the speed of light relative to him, in his observation we might be on the place 1 light-year away after 1 year while keeping our current age, because we keep stopping action in his observation.
If we travel at the speed of light relative to him, in his observation we might be on the place 1 light-year away after 1 year while keeping our current age, because we keep stopping action in his observation.
Traveling is relative. Therefore, the above-mentioned sentences consist even if we replace him and us mutually. Then, contradiction arises. The contradiction can not be solved by psychology like 'A piece of cake of the next person looks large.' The contradiction is called 'Paradox of relativity.'
(1) Established theory and new wrong theory on 'Lorentz contruction' and 'time dilation'
 Inverse Lorenz transformation on infinitesimal space-time intervals
Inverse Lorenz transformation on infinitesimal space-time intervals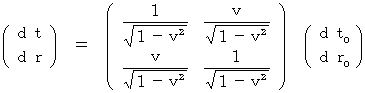
 (Equality 11-1)
(Equality 11-1)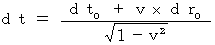
 (Equality 11-2)
(Equality 11-2)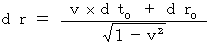
 (Equality 11-3)
(Equality 11-3)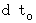

 , owing to (Equation 11-3) we obtain the following
, owing to (Equation 11-3) we obtain the following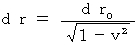
 (Equality 11-4)
(Equality 11-4)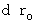

 , owing to (Equation 11-2) we obtain the following
, owing to (Equation 11-2) we obtain the following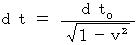
 (Equality 11-5)
(Equality 11-5) Lorenz transformation on infinitesimal space-time intervals
Lorenz transformation on infinitesimal space-time intervals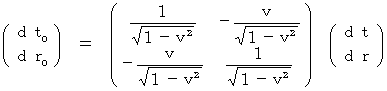
 (Equality 11-6)
(Equality 11-6)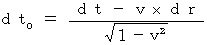
 (Equality 11-7)
(Equality 11-7)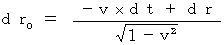
 (Equality 11-8)
(Equality 11-8)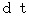

 , owing to (Equation 11-8) we obtain the following
, owing to (Equation 11-8) we obtain the following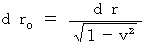
 (Equality 11-9)
(Equality 11-9)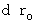

 , owing to (Equation 11-8) we obtain the following
, owing to (Equation 11-8) we obtain the following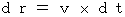
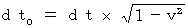
 (Equality 11-10)
(Equality 11-10) A traveling object is short. 'Lorentz contruction'
A traveling object is short. 'Lorentz contruction'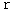
 - coordinate system, we observe space points of
- coordinate system, we observe space points of .
.


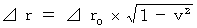

 - coordinate system, we observe space points of
- coordinate system, we observe space points of .
.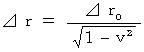
 A traveling object acts slowly ; 'Time dilation'
A traveling object acts slowly ; 'Time dilation'
 - coordinate system, a stationary heart beats once
- coordinate system, a stationary heart beats once .
.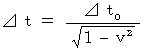
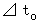 , when it begins to travel.
, when it begins to travel.
 - coordinate system, a stationary clock shows
- coordinate system, a stationary clock shows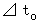 .
.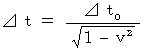
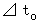 , when it begins to travel.
, when it begins to travel. Time intervals for the observation should
Time intervals for the observation should
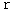
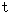 - coordinate system, we observe time points of both
- coordinate system, we observe time points of both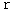
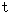 - coordinate system, a tin can telephone is traveling
- coordinate system, a tin can telephone is traveling . A thread of the tin can
. A thread of the tin can . When one of tin cans passes on the space origin, a sound is inputted.
. When one of tin cans passes on the space origin, a sound is inputted. , owing to (Equality 11-7), which belongs to
, owing to (Equality 11-7), which belongs to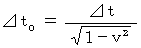


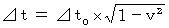
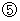 Some points of contradiction
Some points of contradiction - a )
- a ) - b ) .
- b ) . - a )
- a ) - b ) .
- b ) . - b )
- b ) - b ) .
- b ) . - a )
- a ) - a ) .
- a ) . - a )
- a ) - c ) .
- c ) .Stretch of time means time dilation. But, extension of time intervals has no relation to time dilation. Because, it means only that time intervals between the time point on which the event A occurs and the time point on which the event B occurs get longer. Time stretches in a traveling inertial system, and then the ratio of passing time intervals of the traveling inertial system to passing time intervals of an observer's coordinate system is less than
 . We can understand it by imaging as follows :
. We can understand it by imaging as follows : We write scales on a rubber strap stretched moderately. We count the number of scales in certain space intervals, while making the rubber strap be stretched and contracted by turns. Then, we find less number of scales when the rubber strap is stretched.
We write scales on a rubber strap stretched moderately. We count the number of scales in certain space intervals, while making the rubber strap be stretched and contracted by turns. Then, we find less number of scales when the rubber strap is stretched.
By the way, that we feel time long means that we feel passage of time slow.
Stretch of space means extension of space. But, elongation of space intervals has no relation to extension of space. Because, it means only that space intervals between the space point on which the substance A exists and the space point on which the substance B exists get longer. Space contracts in a traveling inertial system, and then the ratio of space intervals of the traveling inertial system to space intervals of an observer's coordinate system is more than
 .
.In a traveling inertial system , i.e. an observed inertial system with space-time coordinates (
 ,
,  ) , with respect to a stationary inertial system , i.e. an observer's inertial system with space-time coordinates (
) , with respect to a stationary inertial system , i.e. an observer's inertial system with space-time coordinates ( 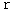 ,
, 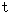 ) , time stretches and space contracts. We can express it with following equalities :
) , time stretches and space contracts. We can express it with following equalities :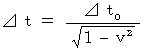
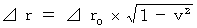
By deforming these equalities, we obtain following equalities, respectively :
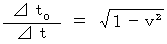
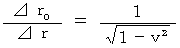
Therefore, we find that the ratio of time intervals of a traveling inertial system to time intervals of an observer's coordinate system is less than
 and the ratio of space intervals of a traveling inertial system to space intervals of an observer's coordinate system is more than
and the ratio of space intervals of a traveling inertial system to space intervals of an observer's coordinate system is more than  .
.Contraction of space means that space intervals through which light travels in an observed inertial system gets shorter. That is, space intervals through which light travels in an observed inertial system per unit time interval of an observer's coordinate system gets shorter than space intervals through which light travels in an observer's inertial system per unit time interval of an observer's coordinate system.
That "Time stretches and space contracts in a traveling inertial system." means that "Time in a traveling inertial system passes more slowly than time in an observer's inertial system, and the speed of light in a traveling inertial system is slower than the speed of light in an observer's inertial system from a standpoint of the observer". Therefore, space intervals through which light travels in a traveling inertial system per unit time interval of the traveling inertial system are equal to space intervals through which light travels in a stationary inertial system per unit time interval of the stationary inertial system. It is just the principle of the constancy of the speed of light.
Then, a new doubt has come. An observed inertial frame of reference does not contract in the perpendicular direction to its movement. Therefore, from a standpoint of the observer, light travels through the observed inertial frame of reference by the same length as light traveling through the observer's inertial frame of reference. So, the speed of light traveling perpendicularly through the observed inertial frame of reference is more than the speed of light traveling through the observer's inertial frame of reference, because time passes slowly in the observed inertial frame of reference. This conclusion denies the principle of constancy of speed of light. So, we bring up 'low of relative vertical speed' to keep the principle of constancy of speed of light. It is an unnatural view to make the interpretation consistent.
(2) Difference between laser and light emitted from a source of light
Please imagine weightless and vacuum space. You are floating and fixed at
 right above a straight rail road track. We set the rail road track to be the X - axis. Please consider that you exist on the origin of coordinate and looking at a telegraph pole which exists a me away on the Y-axis. Now, a train on the rail road track is aproaching you from your left-hand side at a speed of
right above a straight rail road track. We set the rail road track to be the X - axis. Please consider that you exist on the origin of coordinate and looking at a telegraph pole which exists a me away on the Y-axis. Now, a train on the rail road track is aproaching you from your left-hand side at a speed of  . The instant that your friend in the train passes just under you, he/she shots an arrow out to a window towards the telegraph pole at a speed of
. The instant that your friend in the train passes just under you, he/she shots an arrow out to a window towards the telegraph pole at a speed of  relative to him/her.
relative to him/her.Then, you observe that the arrow deflectes at right-hand side of the telegraph pole.
Next, another train is approaching you from your left-hand side at the same speed of
 . When a light source on the roof of the train passes just under you, it emits light for an instant. Then, you observe that the light reaches a telegraph pole after
. When a light source on the roof of the train passes just under you, it emits light for an instant. Then, you observe that the light reaches a telegraph pole after  .
.Notes : You recognize, however, that the light reaches the telegraph pole
 after it was emitted. Because, it takes time intervals of
after it was emitted. Because, it takes time intervals of  that the light on rebound reaches you. Einsten's theory of relativity does not deal with this statement.
that the light on rebound reaches you. Einsten's theory of relativity does not deal with this statement.Now, let us compare the movement of the arrow with the movement of the light in your coordinate system. On one hand, the arrow travels under the influence of the movement of the train when the arrow is just shot. On the other hand, the light travels reguardless of the movement of the train when the light is just emitted. Why do they differ? Where dose this difference come from? To find the answer, we will think about the case that a laser beam is emitted from the moving train toward the telegraph pole instead of the arrow. The speed of the laser beam is
 . Because, by substituting
. Because, by substituting  for
for  of the equation of composition of perpendicular velocities, we obtain
of the equation of composition of perpendicular velocities, we obtain 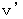

 .
The equation of composition of perperndicular velocities is as follows:
.
The equation of composition of perperndicular velocities is as follows: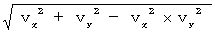
Please see Figure 1103.
Let
 be angle of the movement directin of the laser beam relative to the X-axis.
be angle of the movement directin of the laser beam relative to the X-axis.Then, it is



 . Unless it is
. Unless it is 

 , it is not
, it is not 

 .
.Therefore, we see that the laser beam does not reach the telegraph pole.
Therefore, we see that the laser beam travels under the influence of the movement of the mother when it was just born like an arrow.
Fig.1103

Therefore, that  The speed of light is
The speed of light is 
 is not the reason why the movement of light emitted from a light source is not under the influence of the movement of the mother when it was just born. Then, what is the reason ? It is the reason that light emitted from a light source travels as a wave. That is, true movement form of light emitted from a light source is a surface of an expanding sphere. Nevertheless, since it seems consequently that light travels straightly from one space point to another space point like a particle, it is natural that we think mistakenly the locus of light emitted from a light source is the same as the locus of a laser beam.
is not the reason why the movement of light emitted from a light source is not under the influence of the movement of the mother when it was just born. Then, what is the reason ? It is the reason that light emitted from a light source travels as a wave. That is, true movement form of light emitted from a light source is a surface of an expanding sphere. Nevertheless, since it seems consequently that light travels straightly from one space point to another space point like a particle, it is natural that we think mistakenly the locus of light emitted from a light source is the same as the locus of a laser beam.
When light emitted from a light source aproaches a space point which direction is perpendicular to the direction of motion of the light source, the perpendicular speed of the light becomes slower like an object. However, it is true that the true movement form of light emitted for an instant by a traveling light source is completely the same as the movement form of light emitted by a stationary light source. That is, it is similar to the movement of a surface of an expanding sphere, but is not similar to that of an expanding spheroid which long axis is the same as the locus of a light source. I described that the perpendicular speed of light becomes slower, but I said so only about the 'consequent locus of light' which means that a photon has traveled straightly from one space point to another space point.
(3) Does a traveling object contract ?
Mr.C says :
 Although a traveling object doesn't contract in the vertical direction to the movement , it contracts in the direction of movement, whether it is approaching or getting away. It is called 'Lorentz contraction'.
Although a traveling object doesn't contract in the vertical direction to the movement , it contracts in the direction of movement, whether it is approaching or getting away. It is called 'Lorentz contraction'.
Then, I say to Mr.C :
 Let us think about fundamental relationship between the 1st observer and the 0th observer. Please imagine that there are Mr.A and Ms.B . They keep a stick of the same length in the same horizontal direction, and they are traveling with linear motion in the same direction as the stick at different speed. They compare the length of his/her own stick with the length of the partner's stick each other. To simplify we suppose that three-dimensional space is one dimension.
Let us think about fundamental relationship between the 1st observer and the 0th observer. Please imagine that there are Mr.A and Ms.B . They keep a stick of the same length in the same horizontal direction, and they are traveling with linear motion in the same direction as the stick at different speed. They compare the length of his/her own stick with the length of the partner's stick each other. To simplify we suppose that three-dimensional space is one dimension.Owing to (Equality 5-2) it is as follows :

 (Equality 11-15)
(Equality 11-15)Mr.A is thinking as foolows :
 How longh does Ms.B judge my stick ?
How longh does Ms.B judge my stick ? 
 How longh does Ms.B judge her stick ?
How longh does Ms.B judge her stick ? 
Firstly, let us ask the answer for a ) . Mr.A is the 0th observer. Mr.A observes space points on which both ends of his stick exist at the same time, and then he judges the length of his stick. We suppose that the length of the stationary Mr.A's stick observed by Mr.A is
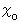
 .
.In this case, by substituting
 for
for 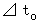 and
and  for
for  of (Equality 11-15), we obtain the following equality:
of (Equality 11-15), we obtain the following equality:
This equality shows the relationship between
 and
and  in Ms.B's coordinate system.
in Ms.B's coordinate system. shows the length of the traveling Mr.A's stick observed by Ms.B .
shows the length of the traveling Mr.A's stick observed by Ms.B . shows the absolute-time intervals between the absolute-time point when Ms.B observes one end of Mr.A's stick and the absolute-time point when Ms.B observes another end of Mr.A's stick.
shows the absolute-time intervals between the absolute-time point when Ms.B observes one end of Mr.A's stick and the absolute-time point when Ms.B observes another end of Mr.A's stick.Owing to above equality, we see easily that it is


 . Therefore, we see that the traveling Mr.A's stick observed by Ms.B is longer than the stationary Mr.A's stick observed by Mr.A . Then, Ms.B thinks that a stationary stick gets longer when it begins to travel. Therefore, it is the answer for a ) that Ms.B judges Mr.A's stick is longer than Ms.B's stick.
. Therefore, we see that the traveling Mr.A's stick observed by Ms.B is longer than the stationary Mr.A's stick observed by Mr.A . Then, Ms.B thinks that a stationary stick gets longer when it begins to travel. Therefore, it is the answer for a ) that Ms.B judges Mr.A's stick is longer than Ms.B's stick.This conclusion is different from Mr.C's view.
Secondly, let us ask the answer for b ) . Mr.A is the 1st observer. Mr.A observes space points on which both ends of Ms.B's stick exist at the same time, and then he judges the length of Ms.B's stick. We suppose that the length of the traveling Ms.B's stick observed by Mr.A is
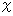
 .
.In this case, by substituting
 for
for  and
and 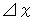 for
for  of (Equality 11-5) , we obtain the following equality:
of (Equality 11-5) , we obtain the following equality: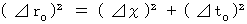
This equality shows the relationship between
 and
and 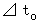 in Ms.B's coordinate system.
in Ms.B's coordinate system. shows the length of the stationary Ms.B 's stick observed by Ms.B .
shows the length of the stationary Ms.B 's stick observed by Ms.B .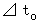 shows the absolute-time intervals between the absolute-time point when Ms.B observes one end of Ms.B's stick and the absolute-time point when Ms.B observes another end of Ms.B's stick.
shows the absolute-time intervals between the absolute-time point when Ms.B observes one end of Ms.B's stick and the absolute-time point when Ms.B observes another end of Ms.B's stick.Owing to above equality, we see easily that it is


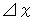 . Therefore, we see that the stationary Ms.B's stick observed by Ms.B is longer than the traveling Ms.B's stick observed by Mr.A. Then, Ms.B thinks that a traveling stick gets longer when it stops. Therefore, it is the answer for b ) that Ms.B judges Ms.B's stick is longer than Mr.A's stick.
. Therefore, we see that the stationary Ms.B's stick observed by Ms.B is longer than the traveling Ms.B's stick observed by Mr.A. Then, Ms.B thinks that a traveling stick gets longer when it stops. Therefore, it is the answer for b ) that Ms.B judges Ms.B's stick is longer than Mr.A's stick.This conclusion is the same as Mr.C's view.
The answer for a ) is quite the opposite to the answer for b ) . A stick gets longer after a coordinate conversion whether it keeps still or travels. It comes from the 'disappearance of simultaneity.' That is, the reason why the answer for a ) is quite the opposite to the answer for b ) is that it is
 bef
bef
 before a coordinate conversion and it is
before a coordinate conversion and it is  aft
aft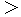
 after the coordinate conversion.
after the coordinate conversion.
We must find space points on which both ends of an object exists at the same time point to measure the length of the object correctly. I call the idea of
 An observer has just illusion because of wrong method of measurement etc.
An observer has just illusion because of wrong method of measurement etc. , as my objection to Mr. C,
, as my objection to Mr. C,  fictitious interpretation of relativity.
fictitious interpretation of relativity. I, however, don't think the idea is right.
I, however, don't think the idea is right.Under the following conditions, is there the time point when a train fits perfectly into a tunnel?

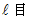

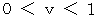
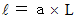
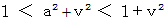
( Answer )
Owing to above-mentioned inequality, we obtain the following inequality :
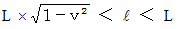
Therefore, we find that the train is certainly longer than the tunnel. So, we find that there is not the time point when a train fits perfectly into a tunnel. Just wait a minute, please. Let us remember 'Lorentz contract.' Then, we find that there is the time point when a train fits perfectly into a tunnel because of the following inequality :
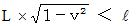
It is
 Paradox of a train and a tunnel.
Paradox of a train and a tunnel. Paradox is something true after well consideration though it seemingly looks false. It is false in the common-sense Newtonian mechanics, but it is true in the theory of relativity which handles the natural phenomenon of the truth. Therefore, it is the paradox. We, however, have some doubts, and we want to say
Paradox is something true after well consideration though it seemingly looks false. It is false in the common-sense Newtonian mechanics, but it is true in the theory of relativity which handles the natural phenomenon of the truth. Therefore, it is the paradox. We, however, have some doubts, and we want to say  It is not paradox but contradiction.
It is not paradox but contradiction. The reason is as follows :
The reason is as follows : The explanation is only from the viewpoint of an observer standing still relative to the tunnel. From the viewpoint of a passenger standing still in the train, tunnel becomes further shorter than the train. So, we find that there is not the time point when a train fits perfectly into a tunnel.
The explanation is only from the viewpoint of an observer standing still relative to the tunnel. From the viewpoint of a passenger standing still in the train, tunnel becomes further shorter than the train. So, we find that there is not the time point when a train fits perfectly into a tunnel.
We can not say as follows as long as we can not object to above mentioned reason of the contradiction :
 It is right that the
It is right that the  paradox of a train and a tunnel
paradox of a train and a tunnel is just paradox.
is just paradox.
To our regret, no one has succeeded in the proof that there is the time point when a train fits perfectly into a tunnel from the viewpoint of a passenger in the train.
(4) Dose the time of the traveling object pass slowly ?
Mr. A says as follows :
 A light, which is emitted perpendicularly from a floor to a ceiling of a spaceship moving parallel to the floor at a speed of
A light, which is emitted perpendicularly from a floor to a ceiling of a spaceship moving parallel to the floor at a speed of  relative to the earth, reaches the ceiling later for you on the earth than for your fried in the spaceship. It reaches the ceiling
relative to the earth, reaches the ceiling later for you on the earth than for your fried in the spaceship. It reaches the ceiling 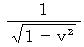 times later on your observation ; its ratio comes from the 'Pythagorean theorem.' Therefore, time of a traveling object passes slowly. So, on the observation of you on the earth, your friend in the traveling spaceship seems to act slowly and grow older slowly. 'Ryugujou' to where 'Taro Urashima' , who is the hero of one of Japanese legends, was taken, is the paradise traveling at the speed of light. He found that he did not grow older at all when he came back to his village after many years. The author of this story had already had a presentiment on the theory of relativity.
times later on your observation ; its ratio comes from the 'Pythagorean theorem.' Therefore, time of a traveling object passes slowly. So, on the observation of you on the earth, your friend in the traveling spaceship seems to act slowly and grow older slowly. 'Ryugujou' to where 'Taro Urashima' , who is the hero of one of Japanese legends, was taken, is the paradise traveling at the speed of light. He found that he did not grow older at all when he came back to his village after many years. The author of this story had already had a presentiment on the theory of relativity.When
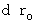

 , owing to the 'infinitesimal inverse Lorentz transformation (Equality 5-1) ' it is as follows :
, owing to the 'infinitesimal inverse Lorentz transformation (Equality 5-1) ' it is as follows :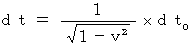
Therefore, we see that the time intervals of
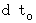 of the 0th observer is converted to the time intervals of
of the 0th observer is converted to the time intervals of 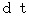 of the 1st observer traveling at a speed of
of the 1st observer traveling at a speed of  relative to the 0th observer.
relative to the 0th observer. 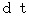 is longer than
is longer than 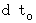 . Therefore, time intervals of the 0th observer are converted to time intervals of the 1st observer, and they become longer. Then, the 1st observer recognizes that the 0th observer's time intervals are longer than the real length. It is not correct expression. Actually, the 0th observer's time intervals observed by the 1st observer are longer than those observed by the 0th observer him/herself.
. Therefore, time intervals of the 0th observer are converted to time intervals of the 1st observer, and they become longer. Then, the 1st observer recognizes that the 0th observer's time intervals are longer than the real length. It is not correct expression. Actually, the 0th observer's time intervals observed by the 1st observer are longer than those observed by the 0th observer him/herself.I introduce the thought experiment to make you understand this statement as follows :
 There are the 1st observer and the 0th observer travling at a speed of
There are the 1st observer and the 0th observer travling at a speed of  relative to the 1st observer. We suppose that both the 1st observer and the 0th observer put on clothes with the same quickness when both of them keep still.
relative to the 1st observer. We suppose that both the 1st observer and the 0th observer put on clothes with the same quickness when both of them keep still.Let
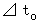 be time intervals taken for the 0th observer to put on clothes.
be time intervals taken for the 0th observer to put on clothes.Let
 be time intervals taken for the 1st observer to observe that the 0th observer puts on clothes.
be time intervals taken for the 1st observer to observe that the 0th observer puts on clothes.Then, dd t is
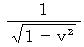 times longer than
times longer than 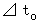 .
.Therefore, the 1st observer recognizes that the 0th observer puts on clothes slowly. It is not only seeming, but also the 0th observer actually puts on clothes more slowly than the 1st observer.


Then, I say to Mr. A as follows :
 Please notice that the traveling is relative. If the relation between you and your friend is the relation between the 0th observer and the 1st observer, the relation between you and your friend is also the relation between the 1st observer and the 0th observer. Therefore, the traveling person is your friend for you, and the traveling person is you for your friend. If the statement :
Please notice that the traveling is relative. If the relation between you and your friend is the relation between the 0th observer and the 1st observer, the relation between you and your friend is also the relation between the 1st observer and the 0th observer. Therefore, the traveling person is your friend for you, and the traveling person is you for your friend. If the statement :  The traveling person puts on clothes more slowly than the stationary person.
The traveling person puts on clothes more slowly than the stationary person. is true, we can not judge which is slow person. It is a paradox.
is true, we can not judge which is slow person. It is a paradox.Now, I show you the 'paradox of triplets returned at different time', which can not be settled by the established theory as the 'paradox of twins traveling symmetorically.'

The 1st brother and the 2nd brother start a space trip at the same time leaving the 3rd brother on the earth. They travel on the same straight line. When their speeds become 80 percent of the speed of light, they travel with linear uniform motion. When they leave the earth, turn up, and return the earth, they change speed with the same acceleration and slowdown. Two and half years for the 3rd brother after the 1st brother had started turning up, the 2nd brother starts turning up.
When the 2nd brother returns the earth, how much different are their ages? We suppose that the 1st brother is 10 years younger than the 3rd brother. Then, how much younger is the 2nd brother than the 3rd brother?
The difference between the trip of the 1st brother and the trip of the 2nd brother is the linear uniform motion for five years for the 3rd brother. Since the 2nd brother travels on linear uniform motion at a speed of 80 percent of the speed of light, meanwhile the 2nd brother gets older the following value times slowly than the 3rd brother:
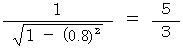
That is, while the 3rd brother has aged by five, the 2nd brother has aged by three. Therefore, the answer is that the 2nd brother is 12 years younger than the 3rd brother.
We find, however, there is a contradicton. The linear uniform motion of the 2nd brother for five years with respect to the 3rd brother is the same as the linear uniform motion of the 3rd brother for five years with respect to the 2nd brother, because of the relativity of traveling. Therefore, while the 2nd brother has aged by five, the 3rd brother has aged by three. So, the answer is that the 2nd brother is 8 years younger than the 3rd brother.
{ Omission }
The 'inverse Lorentz transformation' under the condition of


 shows how long absolute-time intervals (
shows how long absolute-time intervals (  ) changes as a result of a coordinate conversion, when proper time intervals (
) changes as a result of a coordinate conversion, when proper time intervals ( 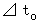 ) are forcely supposed to be fixed ;
) are forcely supposed to be fixed ; 

 is originally absolute,
is originally absolute, 
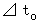
 is originally relative. Since it is
is originally relative. Since it is 

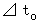 for the 0th observer,
for the 0th observer, 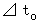 seems to be absolute. Therefore, it is easy to be misunderstood inversely that 'proper time' is absolute and 'absolute-time' is relative.
seems to be absolute. Therefore, it is easy to be misunderstood inversely that 'proper time' is absolute and 'absolute-time' is relative.The 2nd observer is also the 1st observer. That is, the 2nd observer is just the 1st observer as a basic form. When the 1st observer observes the 2nd observer, the points of view of two observers are reversed. That is, the 2nd observer becomes the 1st observer, and the 1st observer becomes the 2nd observer.
Then, a new doubt has come as follows :
 Whenever the 2nd observer observes the time intervals of the 1st observer, time intervals extends surely. Then, conversely when the 1st observer observes time intervals of the 2nd observer, do time intervals extend further more instead of becoming shorter?
Whenever the 2nd observer observes the time intervals of the 1st observer, time intervals extends surely. Then, conversely when the 1st observer observes time intervals of the 2nd observer, do time intervals extend further more instead of becoming shorter? 
After well consideration, the new doubt is right. Because time intervals obtained with a coordinate conversion are illusional. Originally relative-time intervals through which an object travels, like a space intervals through which the object travels, change in length owing to a speed of the object relative to an observer. That is, proper time intervals change as a result of a coordinate conversion. The 'inverse Lorentz transformation', however, asks how absolute-time intervals change in length on the forced condition of constancy of proper time intervals. So, it is natural that time intervals obtained with a coordinate conversion are not realistic. Therefore, when we try to know how we are observed by others, we can get only illusional conclusion.
In order to find a quickness of action or physiological and chemical reaction, including ageing, of an object, you must compare it with a quickness of action or physiological and chemical reaction of yourself. However, two 1st observers compare each other
 Absolute-time intervals after a coordinate conversion
Absolute-time intervals after a coordinate conversion with
with  Absolute-time intervals before the coordinate conversion
Absolute-time intervals before the coordinate conversion , and they recognize the difference between lengthes of absolute-time intervals for observation as the difference between quickness of passage of time. Even if they do it, they say meaninglessly each other as follows :
, and they recognize the difference between lengthes of absolute-time intervals for observation as the difference between quickness of passage of time. Even if they do it, they say meaninglessly each other as follows : This situation looks like as this for me, and it looks like for you as you say. Don't worry.
This situation looks like as this for me, and it looks like for you as you say. Don't worry.

Then, Mr.A asks me repeatedly as follows:
 Are you declare that quickness of an action doesn't change on the case that inverse Lorentz transformation makes time intervals for observation of one heart beet longer?
Are you declare that quickness of an action doesn't change on the case that inverse Lorentz transformation makes time intervals for observation of one heart beet longer?
I answer him flatly as follows:
 Yes. Because, wrong conclusion that Lorentz transformation makes time intervals for observation of one heart beet is led by an unrealistic condition of constancy of proper time.
Yes. Because, wrong conclusion that Lorentz transformation makes time intervals for observation of one heart beet is led by an unrealistic condition of constancy of proper time.
Point of view of the 1st observer, who is a hero/heroin of observers, is not how he/she is observed by others but how he/she observes others and objects. To that purpose, the 1st observer uses a transformation looked like Lorentz transformation from the 1st observer to the 0th observer.' Contrary to Lorentz transformation, this transformation deals with proper time as relative one, and deals with absolute-time as absolute one. this trasformation converts time as follows :
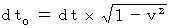
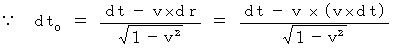
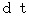 ) to absolute-time intervals of the 0th observer (
) to absolute-time intervals of the 0th observer (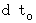 ) .
) .





In contrast to this, a transformation looked like 'Inverse Lorentz transformation from the 0th observer to the 1st observer', which deals with proper time as relative one and absolute-time as absolute one, converts time intervals as foolows :
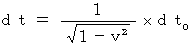
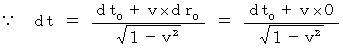
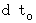 ) to absolute-time intervals of the 1st
) to absolute-time intervals of the 1st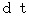 ). And then, it erases the word 'absolute',
). And then, it erases the word 'absolute',





I described in Chapter 4 as follows :
 Inverse Lorentz transformation is more usefull than Lorentz transformasion, because the 1st observer is hero/heroin of observers.
Inverse Lorentz transformation is more usefull than Lorentz transformasion, because the 1st observer is hero/heroin of observers.
The reason why I described like that is that I thought that inverse Lorentz transformation converts 'absolute-time intervals for the observation of the 0th observer' to 'absolute-time intervals for the observation of the 1st observer'. However, I have found that inverse Lorentz transformation has a forced condition that proper time is constant regardless of a coordinate conversion. I was wrong.
The 1st way to escape from a maze of paradox of the relativity is as follows :
 We must free ourselves from the persistence to the comparison between the length of the Minkowsky's space-time of the 0th observer and the length of the Minkowsky's space-time of the 1st observer, and then we must observe from a point of view of the 1st observer in Epstein's space-time. We must throw out once Lorentz transformation, which makes forcely the condition that proper time intervals are constant regardless of a coordinate conversion to find a difference of absolute-time intervals between two inertial systems that means a difference of quickness of the passage of time between two inertial systems.
We must free ourselves from the persistence to the comparison between the length of the Minkowsky's space-time of the 0th observer and the length of the Minkowsky's space-time of the 1st observer, and then we must observe from a point of view of the 1st observer in Epstein's space-time. We must throw out once Lorentz transformation, which makes forcely the condition that proper time intervals are constant regardless of a coordinate conversion to find a difference of absolute-time intervals between two inertial systems that means a difference of quickness of the passage of time between two inertial systems.The relativity comes from what is constant regardless of a coordinate conversion, including the speed of light and physical law. The source of the theory of relativity is following two statements :
Therefore, it is natural that we tend to try to find the difference in length between
 space or time intervals before a coordinate conversion
space or time intervals before a coordinate conversion and
and  space or time intervals after the coordinate conversion.
space or time intervals after the coordinate conversion. We must, however, compare things in the realistic world. In the world, all objects are constantly traveling through four-dimensional space-time at the speed of light. The visible velocity is the 'space velocity' , and the invisible velocity is
We must, however, compare things in the realistic world. In the world, all objects are constantly traveling through four-dimensional space-time at the speed of light. The visible velocity is the 'space velocity' , and the invisible velocity is  relative-time intervals which pass per unit absolute-time interval.
relative-time intervals which pass per unit absolute-time interval. Moreover, all objects are constantly traveling through four-dimensional space-time while keeping a causality of mutual relationship due to collisions of objects, including elementary particle and electro magnetic wave. It is not a promise of human, i.e. rule, but a promise of Got, i.e. natural law. The causality is not broken regardless of a coordinate conversion.
Moreover, all objects are constantly traveling through four-dimensional space-time while keeping a causality of mutual relationship due to collisions of objects, including elementary particle and electro magnetic wave. It is not a promise of human, i.e. rule, but a promise of Got, i.e. natural law. The causality is not broken regardless of a coordinate conversion.Note :
I call 'relative-time passing while absolute-time passes' 'relative-time velocity of an object.' 'Relative-time velocity of an object' corresponds to 'space velocity of an object.'
I think that 'relative-time velocity of an object' don't decide a speed of action or physiological and chemical reaction of an object.
(5) Which is constant regardless of coordinate conversion, proper time or absolute-time ?
To make it easy, we consider space as one dimension. Mr.A, Mr.B, and Mr.C are traveling on linear uniform motion at different speed. Mr.A and Mr.B are observing Mr.C, and Mr.C is observing himself at rest.
 My view :
My view :Absolute-time (

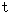 ) is constant regardless of the coordinate conversion.
) is constant regardless of the coordinate conversion.A clock is ticking away absolute- time whether it is traveling or not.
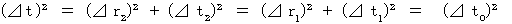
 (Equality 11-22)
(Equality 11-22)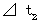 :
: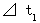
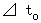
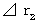
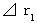
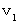
Owing to (Equality 11-22), we obtain
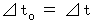
Owing to (Equality 11-22), we obtain the following equality :
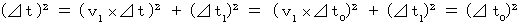
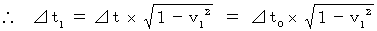

Proper time
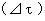 is constant regardless of the coordinate conversion.
is constant regardless of the coordinate conversion.A clock is ticking away proper time whether it is traveling or not.
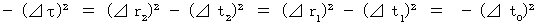
 (Equality 11-16)
(Equality 11-16)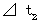
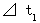
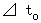
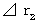
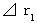
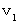
Owing to (Equality 11-16), we obtain
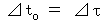
Owing to (Equality 11-16), we obtain the following equality :
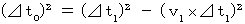
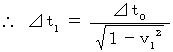
Please imagine one object and many observers traveling on linear uniform motion with various velocities in various directions. Proper time is fixed on an object acting and reacting chemically or physiologically. Proper time intervals are period between two states of action or reaction of an object. As for action and reaction of an object, they have the same contents with respect to all the observers. It is different from a traveling of an object on that point. Action and reaction of an object do not change before and after a coordinate conversion. For example; on one hand, a meat is well done with respect to an observer, on the other hand, the meat is medium with respect to the other observer at the same time; that is impossible. Proper time can not be separated from action and reaction of an object. Proper time intervals do not change before and after a coordinate conversion, because action and reaction of an object do not change before and after a coordinate conversion. It is natural.
In contrast, time of an observer, i.e. coordinate time, is a parameter of action and reaction of an object, and it can be separated from action and reaction of an object; action and reaction of an object follow it. If we show the relation between coordinate time and action or reaction of an object with graph, the horizontal axis is coordinate time, and the vertical axis is action or reaction of an object. Although contents of action and reaction do not change depending on observers, coordinate time intervals in the meantime change depending on observers. Let us make graphs; the horizontal axis is coordinate time and the vertical axis is action or reaction of an object. These graphs have different length of the horizontal axis, depending on observers. Therefore, we see that observed actions and reactions of an object have different quickness, depending on observers.
Time of an observer, i.e. coordinate time, is expressed as follows:

 (Equality 11-17)
(Equality 11-17)
(Equality 11-17) is the same as the following (Equality 11-18):

 (Equality 11-18)
(Equality 11-18)Owing to (Equality 11-18), we obtain the following equality:

 (Equality 11-19)
(Equality 11-19)When the value of proper time intervals to the second power is replaced with the constant number
 , because proper time intervals are constant regardless of coordinate conversion, (Equality 11-19) changes into the following (Equality 11-20):
, because proper time intervals are constant regardless of coordinate conversion, (Equality 11-19) changes into the following (Equality 11-20):
 (Equality 11-20)
(Equality 11-20)(Equality 11-20) makes us find easily that proper time intervals get longer as the traveled space intervals get longer. That is, proper time intervals get longer as the speed gets faster. An object acts or reacts more slowly as the speed of the object gets faster, because that the ratio of coordinate time intervals to proper time intervals gets bigger means that time intervals while the object acts or reacts get longer. (Equality 11-19) makes us find it, too. We find that the quickness of an action or reaction of an object changes depending on observers, because the speed of the object changes depending on observers traveling with various velocities.
As for traveling of light, it must be as follows, because the speed of light, i.e. the speed of photon, is constantly
 with respect to all observers:
with respect to all observers:
 (Equality 11-21)
(Equality 11-21)Owing to (Equality 11-17) and (Equality 11-21) we find the value of the proper time intervals of photon is
 . It means that photon does not act and react.
. It means that photon does not act and react.(6) My space, Your space, and Your spaces
Please notice that the traveled space intervals in (Equality 11-17) are not space intervals of a traveling inertial frame of reference, although proper time intervals are time intervals of a traveling inertial frame of reference. The traveled space intervals belong to a coordinate system of an observer, like 'coordinate time intervals' belong to a coordinate system of an observer. If we consider by mistake the space contracted with 'Lorentz contraction' not as 'traveling local space' but as 'whole space of the observer in which an object is traveling', it is degeneration to the original Lorentz contraction. If we consider by mistake the space contracted with 'Lorentz contraction' not as 'traveling local space' but as 'traveling whole space', it is non-relativistic view that I am absolutely stationary and all things except for me are absolutely traveling. I call this view
 Universal interpretation of Lorentz contraction
Universal interpretation of Lorentz contraction , or
, or  idea of relative traveling whole space except for an observer
idea of relative traveling whole space except for an observer
Mr. A and Ms. B, who appear in special relativity, are traveling with linear uniform motion relatively. Both Mr. A and Ms. B think as follows :
 I'm standing still, and the partner is traveling.
I'm standing still, and the partner is traveling.
Now, I trick you. That is, I take the wrong idea that Mr. A is absolutely traveling and Ms. B stands still absolutely in theory of relativity. I am sure you will be tricked easily. I only set the situation that Mr. A is in a spacecraft and Ms. B is in a space station or the situation that Mr. A is quantum size and Ms. B is planet size, moreover it is effective to add the situation that Mr. C is traveling with the same velocity as Ms. B. As soon as you are tricked, Mr. A starts absolutely growing older slowly, and only the standpoint of Mr. A begans to follow
 idea of relative traveling whole space except for an observer.
idea of relative traveling whole space except for an observer.
The established idea that 'Elongation of life of muon is the evidence that theory of relativity is right.' is wrong, because it is explained with this trick. Muon can not come to the grand of the earth before it dies. With respect to an observer on the grand of the earth with the same remaining days as muon, however, it can come after the death of the observer because of elongation of its life. Plus, with respect to the muon, it can meet the observer before their death because of Lorentz contraction of whole space observed by the muon.
(7) Over-interpretation in
 the way of electromagnetic wave to find Lorentz transformation
the way of electromagnetic wave to find Lorentz transformation
Although I described that proper time is a magnitude of relative-time, I will clarify the difference between them. For example, on one hand, proper time has a image of time that each object has, on the other hand, relative-time has a image of time observed by others. I will explain the difference between proper time and relative-time, while comparing them with absolute-time.
Each observer or object is gifted with absolute-time. Absolute-time is common time. All movements ( traveling, action, physiological and chemical reaction etc. ) of all objects follow absolute-time. In contrast to this, relative-time is one of axis of four-dimensional space-time. It depens on an observation. A kinetic relationship between an object and observer determins traveling relative-time intervals of the object. Traveling space of an object is the same as this. It is said that there is no 'Absolute state of non-traveling.' Therefore, we can say similary as follows :
 There is no 'Absolute state of non-traveling in the relative-time direction.'
There is no 'Absolute state of non-traveling in the relative-time direction.'
There is no idea of relative-time in the established theory. Instead there is an idea of proper time in the established theory.
The established theory explains proper time as follows :
 A moved distance of an object changes owing to how to be observed. That is, traveling space intervals of an object change in length because of a coordinate conversion. Proper time intervals, however, don't change in length because of a coordinate conversion. It is a speed of passage of proper time that changes. When many objects are traveling in an inertial coordinate system, speeds of passages of proper times of each object are different. A speed of passage of proper time of an object decides a speed of action or physiological and chemical reaction of the object. A speed of passage of proper time of an object is decided depending on the ratio to coordinate time intervals of proper time intervals during an action or a traveling of the object. Coordinate time is the same in all space points of an observer. 'Coordinate time' is time of coordinates. Coordinate time points of all space points are equal. In contrast, 'proper time' is Coordinate time is time of coordinates. Coordinate time points of all space points are equal. In contrast, proper time is time of a traveling spot. Proper time points of traveling spots are individual. Since proper time is the same as coordinate time of the 0th observer, proper time is the time of coordinates of the 0th observer. So, we must use the word of 'proper time' after we see whether it belongs to the 1st observer or the 0th observer. In order to avoid confusion, we must say 'coordinate time of the 0th observer' instead of saying 'proper time of the 0th observer'.
A moved distance of an object changes owing to how to be observed. That is, traveling space intervals of an object change in length because of a coordinate conversion. Proper time intervals, however, don't change in length because of a coordinate conversion. It is a speed of passage of proper time that changes. When many objects are traveling in an inertial coordinate system, speeds of passages of proper times of each object are different. A speed of passage of proper time of an object decides a speed of action or physiological and chemical reaction of the object. A speed of passage of proper time of an object is decided depending on the ratio to coordinate time intervals of proper time intervals during an action or a traveling of the object. Coordinate time is the same in all space points of an observer. 'Coordinate time' is time of coordinates. Coordinate time points of all space points are equal. In contrast, 'proper time' is Coordinate time is time of coordinates. Coordinate time points of all space points are equal. In contrast, proper time is time of a traveling spot. Proper time points of traveling spots are individual. Since proper time is the same as coordinate time of the 0th observer, proper time is the time of coordinates of the 0th observer. So, we must use the word of 'proper time' after we see whether it belongs to the 1st observer or the 0th observer. In order to avoid confusion, we must say 'coordinate time of the 0th observer' instead of saying 'proper time of the 0th observer'.
The established theory explains a speed of passage of proper time of an object as follows:
 Please imagine that you are observing a stationary clock A and a traveling clock B on uniform motion. Your friend is traveling with the same velocity of the clock B.
Please imagine that you are observing a stationary clock A and a traveling clock B on uniform motion. Your friend is traveling with the same velocity of the clock B.A speed of ticking away of the clock B with respect to you is slower than a speed of ticking away of the clock B with respect to your friend. It depends on the ratio to coordinate time intervals of proper time intervals.
There are following traveling times while the point of the hand of the clock B travels from 0 minute to 1 minute.




Owing to
 ,
,  , and
, and 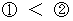 , we obtain
, we obtain 
Owing to
 and
and 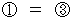 , we obtain the following expression:
, we obtain the following expression: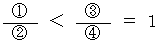
Therefore, we find that a speed of ticking away of the clock B with respect to you is slower than a speed of ticking away of the clock B with respect to your friend.
In your standpoint, a speed of ticking away of the clock B is slower than a speed of ticking away of the clock A.
In order to find how slowly a clock is ticking away, firstly we find how long proper time of the clock passes while one coordinate time passes, secondly we find the ratio to the coordinate time intervals of the proper time intervals, finally we compare the ratio to 1.
To find how long proper time of a clock passes, we find where a point of a hand of the clock travels from 0 minute.
To find how long coordinate time passes, we find where a point of a hand of a stationary clock travels from 0 minute.
There are following traveling times while a point of a hand of the traveling clock B travels from 0 minute.


The Value of
 is 1 minute.
is 1 minute.To find the value of
 , we find where a point of a hand of the stationary clock A travels from 0 minite. Then, we find the value of
, we find where a point of a hand of the stationary clock A travels from 0 minite. Then, we find the value of  is over 1 minute.
is over 1 minute.There are following traveling times while a point of a hand of the stationary clock A travels from 0 minute to 1 minute.


The Value of
 is 1 minute.
is 1 minute.To find the value of
 , we find where a point of a hand of a stationary clock A travels from 0-minite. Then, we find the value of
, we find where a point of a hand of a stationary clock A travels from 0-minite. Then, we find the value of  is 1 minute.
is 1 minute.So, we obtain the following expression:

Therefore, we find that a speed of ticking away of the clock B is slower than a speed of ticking away of the clock A in your standpoint.
As mentioned above, the reason why a speed of action or physiological and chemical reaction changes owing to how to be observed is that the ratio to coordinate time of proper time of an object changes relatively owing to how to be observed.

Now, let us see the birth of the idea of proper time.
I show the equality looked like an equality derived by 'Infinitestimal inverse Lorentz transformation' as follows.
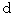 is replaced with
is replaced with 
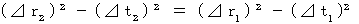
 (Equality 11-24)
(Equality 11-24)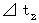 is absolute-time intervals of the 2nd observer.
is absolute-time intervals of the 2nd observer.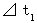 is absolute-time intervals of the 1st observer.
is absolute-time intervals of the 1st observer.This equation showes what a traveling of an object observed by the 2nd observer and a traveling of the object observed by the 1st observer have in common. That is, (Equality 11-24) showes as follows :
 When two observers traveling at different speed relative to an object observe the object at the same time, the length of 'proper time in a wide sense
When two observers traveling at different speed relative to an object observe the object at the same time, the length of 'proper time in a wide sense 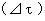 ' is equal for two observers.
' is equal for two observers.
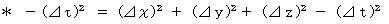
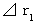

 ,
, 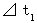 is proper
is properOwing to ( Equality 11-24), we obtain
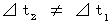 , because it is
, because it is 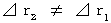 . Therefore, absolute-time intervals of the 2nd observer are not equal to absolute-time intervals of the 1st observer. So, a usual idea of absolute-time was overturned. When we compare a traveling of an object in one inertial system with a traveling of the object in another inertial system, on one hand, proper time intervals are equal, on the other hand, time intervals are not equal. Therefore, it is the accepted view that proper time is absolute and time is relative.
. Therefore, absolute-time intervals of the 2nd observer are not equal to absolute-time intervals of the 1st observer. So, a usual idea of absolute-time was overturned. When we compare a traveling of an object in one inertial system with a traveling of the object in another inertial system, on one hand, proper time intervals are equal, on the other hand, time intervals are not equal. Therefore, it is the accepted view that proper time is absolute and time is relative.(Equality 11-24) appears in the process of finding Lorentz transformation with modern standard method. I mentioned the following equations in Chapter 4 :
Owing to
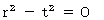 and
and 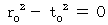 , it is as follows:
, it is as follows: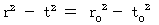
 (Equation 11-25)
(Equation 11-25)The left hand side of (Equality 11-25) is the coordinate system of the 2nd observer, and the right hand side is the coordinate system of the 1st observer.
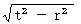 shows proper time intervals of light observed by the 2nd observer. If I express this, it shows traveling relative-time intervals of light observed by the 2nd observer. It's value is
shows proper time intervals of light observed by the 2nd observer. If I express this, it shows traveling relative-time intervals of light observed by the 2nd observer. It's value is  .
.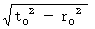 shows proper time intervals of light observed by the 1st observer. If I express this, it shows traveling relative-time intervals of light observed by the 1st observer. It's value is
shows proper time intervals of light observed by the 1st observer. If I express this, it shows traveling relative-time intervals of light observed by the 1st observer. It's value is  .
.(Equality 11-24) and (Equality 11-25) shows the same content.
The Modern standard method to find Lorentz trasformation develops a theory after considering that this equality might apply to travels of all objects.
Now, we consider the standard method logically. Please notice the following facts :
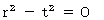
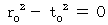
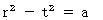
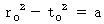
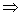
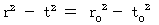
Let the set A' be all combinations of four signs
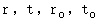 applying to the fact A.
applying to the fact A.Let the set B' be all combinations of four signs applying to the fact B.
When we select one of combinations of four signs in a certain range at random, if the combination certainly applies to the fact A, we consider that the fact A is 'the law in the range.'
In this case, the following proposition is true :
 If the combination of four signs applies to the fact A, it certainly applies to the fact B.
If the combination of four signs applies to the fact A, it certainly applies to the fact B.
And, the following proposition is false :
 If the combination of four signs applies to the fact B, it certainly applies to the fact A.
If the combination of four signs applies to the fact B, it certainly applies to the fact A.
Then, we express as follows :
 The necessary condition that the combination of four signs applies to the fact A is that the combination of four signs applies to the fact B.
The necessary condition that the combination of four signs applies to the fact A is that the combination of four signs applies to the fact B.
 The sufficient condition that the combination of four signs applies to the fact B is that the combination of four signs applies to the fact A.
The sufficient condition that the combination of four signs applies to the fact B is that the combination of four signs applies to the fact A.
In this case, the following propositions are true :
 The set A' is a subset of the set B'.
The set A' is a subset of the set B'.
 The set B' includes the set A'.
The set B' includes the set A'.
In this case, the following proposition is true :
 If the fact A is the law in a certain range, the fact B is the law in the range.
If the fact A is the law in a certain range, the fact B is the law in the range.
And, the following proposition is false :
 If the fact B is the law in a certain range, the fact A is the law in the range.
If the fact B is the law in a certain range, the fact A is the law in the range.
Then, we express as follows :
 The necessary condition that the proposition:
The necessary condition that the proposition: The fact A is the law in a certain range.
The fact A is the law in a certain range. is true is that the proposition:
is true is that the proposition: The fact B is the law in the range.
The fact B is the law in the range. is true.
is true.
 The sufficient condition that the proposition:
The sufficient condition that the proposition: The fact B is the law in a certain range.
The fact B is the law in a certain range. is true is that the proposition:
is true is that the proposition: The fact A is the law in the range.
The fact A is the law in the range. is true.
is true.
By the way the following proposition is false :
 If the fact A is the law in a certain range, the fact A is the law in a wider range including the range.
If the fact A is the law in a certain range, the fact A is the law in a wider range including the range.
Do you think the following proposition is true or false?
 If the fact A is the law in a certain range, the fact B is the law in a wider range including the range.
If the fact A is the law in a certain range, the fact B is the law in a wider range including the range.
Of course, the answer is false. Actually, the standard method to find Lorentz transformation is similar to this proposition. The standard method to find Lorentz transformation expands the range of travel of light to the range of travel of objects. The standard method to find Lorentz transformation, however, says as follows :
 Since the fact A is the law in a certain range, the fact B is the law in the range.
Since the fact A is the law in a certain range, the fact B is the law in the range.
By rights, the standard method should say as follows :
 We can suppose that the fact B is the law in a wider range including the range. Because, the fact A is the law in the range, and the necessary condition that the proposition: 'The fact A is the law in the range.' is true is that the proposition: 'The fact B is the law in the range.' is true.
We can suppose that the fact B is the law in a wider range including the range. Because, the fact A is the law in the range, and the necessary condition that the proposition: 'The fact A is the law in the range.' is true is that the proposition: 'The fact B is the law in the range.' is true.
What standard method says disguises that the range is enlarged. So, we misunderstand that the set A is equal to the set B. Therefore, we will not see through illogicality easily.
* The wrong logic
 The first setting :
The first setting :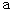 is equal to
is equal to 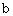 .
.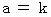 and
and 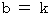
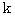 is an optional number.
is an optional number. The necessary and sufficient condition of
The necessary and sufficient condition of  is
is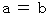 .
. The necessary condition of
The necessary condition of  is
is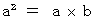 .
. is
is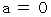 and
and 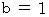 .
. The necessary and sufficient condition of
The necessary and sufficient condition of  is
is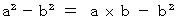 .
.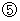 The necessary and sufficient condition of
The necessary and sufficient condition of  is
is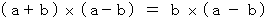 .
.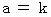 and
and 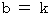
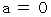 and
and 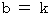
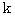 is an optional number.
is an optional number. We must not think as follows, because we must not divide by
We must not think as follows, because we must not divide by  :
: The necessary condition of
The necessary condition of 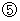 is
is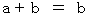 .
.
 If we think as
If we think as  ,
,  is over-interpretation,
is over-interpretation, If we thing as
If we thing as  , the conclusion does not deny
, the conclusion does not deny is the sufficient condition.
is the sufficient condition.
 is the 'logical mistake'. The logic including some 'logical
is the 'logical mistake'. The logic including some 'logical Though the logic for finding 'Lorentz transformation' includes
Though the logic for finding 'Lorentz transformation' includesWe can keep a premise by thinking logically from the outside to the inside as follows :
 The premise applies to the proposition, because it applies to the necessary condition of the proposition.'
The premise applies to the proposition, because it applies to the necessary condition of the proposition.'
 The premise is true in this range, because it is true in a wider range including this range.
The premise is true in this range, because it is true in a wider range including this range.
But, if we think it in the opposite direction, the premise becomes to do not apply to a certain case, because the reverse is not necessarily true.
Mistake like this is called
 over-interpretation.
over-interpretation. However,
However,  over-interpretation
over-interpretation itself is not bad. It produces imagination to create something new. It is the same as an assumption. There is no problem as long as it is made clear that there is an assumption.
itself is not bad. It produces imagination to create something new. It is the same as an assumption. There is no problem as long as it is made clear that there is an assumption.It is assumed as follows in the standard method :
Two inertial systems are relatively traveling on linear uniform motion. When space-time origins of two inertial systems pile up, light is emitted. The loci of light in two inertial systems are shown with following expressions, respectively :

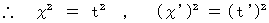


Then, it is assumed that motions of all objects in two inertial systems are shown with following expressions, respectively:
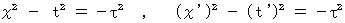
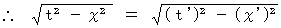
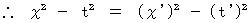
The modern standard method to find Lorentz transformation, i.e. finding method of Lorentz transformation with electromagnetic wave, is based on a hypothesis. The hypothesis is as follows :
 In two inertial frames of reference traveling relatively with linear uniform motion, proper time intervals, i.e. traveling space-time intervals, of an observed object are constant. Proper time is a realistic passed time in the inertial frame of reference; for example a heart beats once.
In two inertial frames of reference traveling relatively with linear uniform motion, proper time intervals, i.e. traveling space-time intervals, of an observed object are constant. Proper time is a realistic passed time in the inertial frame of reference; for example a heart beats once.
Lorentz transformation was originally made based on the principle of relativity, i.e. axiom No.1, on electromagnetics to keep Maxwell's equations be satisfied regardless of a coordinate conversion. I call this way of finding Lorentz transformation 'finding method of Lorentz transformation with electromagnetic field.' After that, Einstein worked out Lorentz transformation from the principle of constancy of the speed of light, i.e. axiom No.2. I call this way of finding Lorentz transformation 'finding method of Lorentz transformation with electromagnetic wave.' After that, future generations simplified his method to establish the modern standard method to find Lorentz transformation. Therefore, it is wrong that we deny the theory of relativity because of non-logicality of 'finding method of Lorentz transformation with electromagnetic wave.' We can not deny the theory of relativity as long as we prove that 'finding method of Lorentz transformation with electromagnetic field' is not logical.
Lorentz transformation, which is the root of relativity, affirms proper time and denies absolute-time. Lorentz transformation has two problems on practice. One of them is that Lorentz transformation makes some contradictions, and the other is that no experiment has proved whether the way of useing Lorentz transformation is right or not, because of difficulty of experiment. Lorentz transformation has a theoretical problem, too. It is that Lorentz transformation is not a congruent transformation. It means that Lorentz transformation is not recognized officially as a coordinate conversion in physics. Introduction of imaginary time, however, makes Lorentz transformation be recognized as a coordinate conversion in physics.
A coordinate conversion in physics is a linear transformation which keeps intervals of two space points constant. It is called congruent transformation. Rectangular matrix bears a coordinate conversion in physics; product of rectangular matrix and its transposes is a unit matrix. The matrix of Lorentz transformation is not a rectangular matrix. However, if we deal with time as imaginary time and reform the matrix of Lorentz transformation as follows, it becomes a rectangular matrix to make Lorentz transformation be a coordinate conversion in physics :
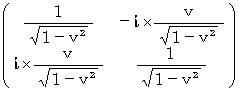
I call this matrix 'Complex number Lorentz transformation.' If we consider electric field as follows, Maxwell's equations are satisfied regardless of Complex number Lorentz transformation :
 Electric field is imaginary components of electromagnetic field. It is produced by an electric charge traveling through imaginary time at a speed of light, and then it exerts influence on another electric charge traveling through imaginary time at a speed of light.
Electric field is imaginary components of electromagnetic field. It is produced by an electric charge traveling through imaginary time at a speed of light, and then it exerts influence on another electric charge traveling through imaginary time at a speed of light.
Therefore, special theory of relativity without contradiction seems to be established.
I think that we do not need imaginary time in physics. Therefore, I think that Lorentz transformation is not a coordinate conversion. I think as follows :
 Relativistic coordinate conversion keeps magnitude of position vector of space-time point ( space point, relative-time point ) constant. However, space-time point is limited to one on which an object, including photon, traveling with linear uniform motion after passing space-time origin, can exist.
Relativistic coordinate conversion keeps magnitude of position vector of space-time point ( space point, relative-time point ) constant. However, space-time point is limited to one on which an object, including photon, traveling with linear uniform motion after passing space-time origin, can exist.Relativistic coordinate conversion is a coordinate conversion between two observers who are equal. In this sense, equal has two means. One of them is that two observes are traveling with linear uniform motion and then we can not tell which is traveling and which stands still. The other is that their observations start at the same time when they and an observed object are on the same space point.
I think Lewis Carroll Epstein assumed as follows :
Two inertial systems are relatively traveling on linear uniform motion. When space-time origins of two inertial systems pile up, light is emitted. The loci of light in two inertial systems are shown with following expressions, respectively :


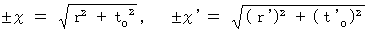 .
.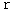 is space, and
is space, and  is proper time which is the
is proper time which is the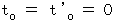 .
.
 (Equality 11-26)
(Equality 11-26)Taking over his assumption, I thought as follows :
All objects must get elder with equal quickness. So, it must be not proper time but absolute-time that prescribes motions and actions of all objects. Therefore, (Equality 11-26) is as follows :
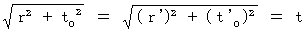
 (Equality 11-27)
(Equality 11-27)In case of light, the following equality is right :
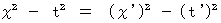
So, in case of light, Lorentz transformation is right. Therefore, in case of light, the following equation of composition of velocities is right :
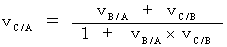
 (Equality 11-28)
(Equality 11-28)Then, I assume as follows :
 The equation of composition of velocities
The equation of composition of velocities
The object C is traveling on linear uniform motion at a speed of
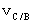 relative to the 1st observer B. The 2nd observer A is traveling on linear uniform motion at a speed of
relative to the 1st observer B. The 2nd observer A is traveling on linear uniform motion at a speed of  relative to the 1st observer B in the opposite direction of the object C relative to the 1st observer B. How does the 2nd observer A observe the object C ?
relative to the 1st observer B in the opposite direction of the object C relative to the 1st observer B. How does the 2nd observer A observe the object C ?Owing to (Equality 11-27) , we obtain the following equality:
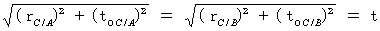
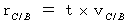
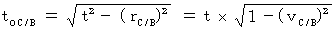
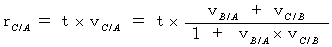

If we express space-time coordinates as ( space coordinates, relative-time coordinate ), coordinate conversion is expressed as follows:
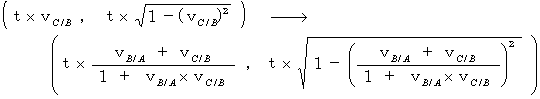
When the object C is the observer B, especially, the coordinate conversion from the 0th observer B to the 1st observer A is expressed as follows:
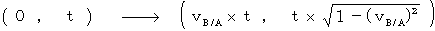
This coordinate conversion is a root of my inertial systems theory of relativity. It keeps the speed of light constant, it does not make a speed of object more than the speed of light, and it keeps absolute-time intervals (

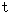 ) constant. I will describe about this coordinate conversion in the next chapter.
) constant. I will describe about this coordinate conversion in the next chapter.