Chapter 12 Abandonment of Observation of a Third Party and New Transformation
Abandonment of Observation of a Third Party and New Transformation
(1)
First, I explain the difference between 'the velocity on a subjective observation from a standview of the person concerned' and 'the velocity on a subjective observation from a standview of a third party'. 'An observation from a standview of the person concerned' is done when something that is standard of content of observation is not moving. 'An subjective observation' is done with a scale of time and space that the observer is carrying.
Please imagine vacuum and weightless universe. There is a very wide plain mirror in the far distance. Goro uses a flash. After
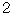
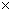
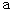
 , he observes the reflection of flashlight. When he uses a flash, there is Tomoko on his back; she is traveling with linear uniform motion parallel to the mirror. After
, he observes the reflection of flashlight. When he uses a flash, there is Tomoko on his back; she is traveling with linear uniform motion parallel to the mirror. After 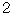
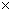 (
( 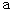
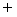
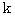 )
)  , she sobserves the reflection of flashlight.
, she sobserves the reflection of flashlight.The flashlight spreads in the shape of sphere at a speed of
 . The obit of flashlight observed by Tomoko is different from the obit of flashlight observed by Goro. Their hearts beat once between the flashlight is emitted and the reflection of the flashlight is observed.
. The obit of flashlight observed by Tomoko is different from the obit of flashlight observed by Goro. Their hearts beat once between the flashlight is emitted and the reflection of the flashlight is observed.We can consider that Tomoko keeps still and Goro is traveling, because their kinetic relationship is relative and symmetrical. In this case, the mirror and the flash are traveling with respect to Tomoko. Nevertheless, the movements of flashlight relative to them are completely symmetrical for them. Therefore, On the Tomoko's observation, her heart beats once for
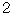
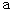
 , and Goro's heart beats once for
, and Goro's heart beats once for 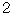
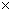 (
( 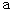
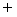
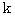 )
)  .
.We find four conclusions out of this thought experiment as follows :
Conclusion 1 :
 Traveling distance of flashlight to approach Tomoko with respect to Goro
Traveling distance of flashlight to approach Tomoko with respect to Goro is longer than
is longer than  traveling distance of flashlight to approach Goro with respect to Goro.
traveling distance of flashlight to approach Goro with respect to Goro. So, on the Goro's observation, Tomoko sees the reflection of flashlight later than Goro. Therefore, we see that a traveling person acts more slowly than a stationary person.
So, on the Goro's observation, Tomoko sees the reflection of flashlight later than Goro. Therefore, we see that a traveling person acts more slowly than a stationary person.Conclusion 2 :
 Traveling distance of flashlight to approach Goro with respect to Tomoko
Traveling distance of flashlight to approach Goro with respect to Tomoko is longer than
is longer than  traveling distance of flashlight to approach Tomoko with respect to Tomoko
traveling distance of flashlight to approach Tomoko with respect to Tomoko So, on the Tomoko's observation , Goro sees the reflection of flashlight later than Tomoko. Therefore, we see that a traveling person acts more slowly than a stationary person.
So, on the Tomoko's observation , Goro sees the reflection of flashlight later than Tomoko. Therefore, we see that a traveling person acts more slowly than a stationary person.Conclusion 3 :
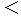 | Vg^L(g)g |
| Vg^L(g)g |The direction of
 relative velocity of flashlight approaching Tomoko relative to Tomoko with respect to Goro ( Vg^L(t)t )
relative velocity of flashlight approaching Tomoko relative to Tomoko with respect to Goro ( Vg^L(t)t ) is the same as the direction of
is the same as the direction of  velocity of flashlight approaching Goro with respect to Goro as a person concerned ( Vg^L(g)g ) .
velocity of flashlight approaching Goro with respect to Goro as a person concerned ( Vg^L(g)g ) . The magnitude of Vg^L(g)t is smaller than Vg^L(g)g ; the magnitude of Vg^L(g)g is
The magnitude of Vg^L(g)t is smaller than Vg^L(g)g ; the magnitude of Vg^L(g)g is  . So, on the Goro's observation, Tomoko sees the reflection of flashlight later than Goro. Therefore, we see that a traveling person acts more slowly than a stationary person.
. So, on the Goro's observation, Tomoko sees the reflection of flashlight later than Goro. Therefore, we see that a traveling person acts more slowly than a stationary person.Conclusion 4 :
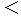 | Vt^L(t)t |
| Vt^L(t)t |The direction of
 relative velocity of flashlight approacging Goro relative to Goro with respect to Tomoko ( Vt^L(g)g )
relative velocity of flashlight approacging Goro relative to Goro with respect to Tomoko ( Vt^L(g)g ) is the same as the direction of
is the same as the direction of  velocity of flashlight approaching Tomoko with respect to Tomoko as a person concerned ( Vt^L(t)t ).
velocity of flashlight approaching Tomoko with respect to Tomoko as a person concerned ( Vt^L(t)t ). The magnitude of Vt^L(g)g is smaller than Vt^L(t)t ; the magnitude of Vt^L(t)t is
The magnitude of Vt^L(g)g is smaller than Vt^L(t)t ; the magnitude of Vt^L(t)t is  . So, on the Tomoko's observation, Goro sees the reflection of flashlight later than Tomoko. Therefore, we see that a traveling observer sees the reflection of flashlight later than a stationary observer.
. So, on the Tomoko's observation, Goro sees the reflection of flashlight later than Tomoko. Therefore, we see that a traveling observer sees the reflection of flashlight later than a stationary observer. velocity of Tomoko
velocity of Tomoko from
from velocity of flashlight approaching Tomoko relative to
velocity of flashlight approaching Tomoko relative to in vector space.
in vector space.I express
 Velocity of H relative to b with respect to a
Velocity of H relative to b with respect to a

 In the subjective observation of a from a standpoint of a third party, Velocity of H relative to looked-like-traveling b
In the subjective observation of a from a standpoint of a third party, Velocity of H relative to looked-like-traveling b with Va^Hb . I call it
with Va^Hb . I call it  third party's relative velocity.
third party's relative velocity. When it is Va^Ha , it is
When it is Va^Ha , it is  velocity with respect to the person concerned.
velocity with respect to the person concerned. When it is the velocity of light, we use L instead of H . The magnitude of Va^La is always
When it is the velocity of light, we use L instead of H . The magnitude of Va^La is always  . The magnitude of Va^Lb is
. The magnitude of Va^Lb is  or more, and
or more, and 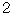 or less. It seems to disobey
or less. It seems to disobey  principle of constancy of speed of light.
principle of constancy of speed of light. Nevertheless, it is not illogical, because
Nevertheless, it is not illogical, because  A third party's relative velocity
A third party's relative velocity doesn't exist really, and it is imaginary velocity.
doesn't exist really, and it is imaginary velocity.Va^Hb is different from Ia^Hb, which shows
 In the objective observation of a from a standpoint of the person concerned, Velocity of H relative to looked-like-stationary b .
In the objective observation of a from a standpoint of the person concerned, Velocity of H relative to looked-like-stationary b . Ia^Hb is measured with a scale and a clock belonging to b . In contrust, Va^Hb is measured with a stationary scale and a stationary clock relative to the observer.
Ia^Hb is measured with a scale and a clock belonging to b . In contrust, Va^Hb is measured with a stationary scale and a stationary clock relative to the observer.Second, Let us think about the difference between 'subjective velocity from a standpoint of a third party' and 'objective velocity from a standpoint of the person concerned'
When there are one observed object and three observers, i.e. the 0th observer, the 1st observer, and the 2nd observer, there are the following velocities :
Proviso,
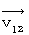 :
:In the subjective observation of the 2nd observer from a standpoint of the person concerned, Velocity of the 1st observer relative to the looked-like-stationary 2nd observer
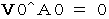
In the subjective observation of the 0th observer from a standpoint of the person concerned, Velocity of the object A relative to the looked-like-stationary 0th observer
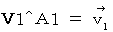
In the subjective observation of the 1st observer from a standpoint of the person concerned, Velocity of the object A relative to the looked-like-stationary 1st observer
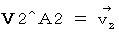
In the subjective observation of the 2nd observer from a standpoint of the person concerned, Velocity of the object A relative to the looked-like-stationary 2nd observer
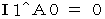
In the objective observation of the 1st observer from a standpoint of the person concerned, Velocity of the object A relative to the looked-like-stationary 0th observer

In the objective observation of the 2nd observer from a standpoint of the person concerned, Velocity of the object A relative to the looked-like-stationary 0th observer
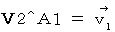
In the subjective observation of the 2nd observer from a standpoint of a third party, Velocity of the object A relative to the looked-like-traveling 1st observer
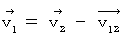 , we obtain the following equality :
, we obtain the following equality :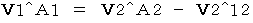
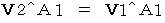
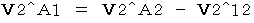
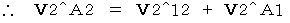
 (Equality 1201)
(Equality 1201)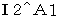 :
:In the objective observation of the 2nd observer from a standpoint of the person concerned, Velocity of the object A relative to the looked-like-stationary 1st observer
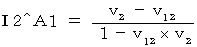
The theory of relativity does not accept just one of these seven velocities. It is
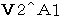 . The theory of relativity considers 'observation from a standpoint of a third party' as non-realistic observation.。 For example, the speed of the object A relative to the 1st observer by 'observation from a standpoint of a third party' is
. The theory of relativity considers 'observation from a standpoint of a third party' as non-realistic observation.。 For example, the speed of the object A relative to the 1st observer by 'observation from a standpoint of a third party' is 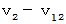 , and the speed of the object A relative to the 1st observer by 'observation from a standpoint of the person concerned' is
, and the speed of the object A relative to the 1st observer by 'observation from a standpoint of the person concerned' is 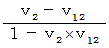 ; they are different. If we use 'observation from a standpoint of a third party' in the theory of relativity, some contradictions appear. So, we think the theory of relativity is wrong, but its view is wrong.
; they are different. If we use 'observation from a standpoint of a third party' in the theory of relativity, some contradictions appear. So, we think the theory of relativity is wrong, but its view is wrong.We regard an observed object as traveling in 'observation from a standpoint of a third party', and we regard an observed object as being stationary in 'observation from a standpoint of the person concerned'. We use a stationary scale and a stationary clock relative to an observer in
 subjective observation', and we use 'a scale and a clock belonging to an object, which is the standard of an observation, with respect to an observer
subjective observation', and we use 'a scale and a clock belonging to an object, which is the standard of an observation, with respect to an observer in 'objective observation'.
in 'objective observation'. By the way, I call the following view ' fictitious interpretation of the relativity' :
 We must use a scale and a clock belonging to an observed object to observe the proper time point and the proper space point on which the object exists. If we use a stationary scale and a stationary clock relative to an observer to observe a traveling object, we have only fictitious observation. Lorentz transformation serves us the proper image from the fictitious image.
We must use a scale and a clock belonging to an observed object to observe the proper time point and the proper space point on which the object exists. If we use a stationary scale and a stationary clock relative to an observer to observe a traveling object, we have only fictitious observation. Lorentz transformation serves us the proper image from the fictitious image.
Incidentally, I think it is wrong to solve contradictions with 'fictitious interpretation of the relativity.'
Coordinate conversion is done with Galilean transformation in Newtonian mechanics, which has absolute space-time. In Newtonian mechanics, 'observation from a standpoint of a third party, i.e.

 relative to traveling
relative to traveling 
 ' is the same as 'observation from a standpoint of the person concerned, i.e.
' is the same as 'observation from a standpoint of the person concerned, i.e. 
 relative to stationary
relative to stationary 
 '. In the theory of relativity, Coordinate conversion is done with Lorentz transformation. Theory of relativity does not accept 'observation from a standpoint of a third party', and it accepts only 'observation from a standpoint of the person concerned.' 'Observation from a standpoint of the person concerned' has two patterns. One of them is 'Subjective observation from a standpoint of the person concerned', which is an observation of observer about him/herself. The other is 'Objective observation from a standpoint of the person concerned', which is an observation of observer about other from a viewpoint of the person concerned.
'. In the theory of relativity, Coordinate conversion is done with Lorentz transformation. Theory of relativity does not accept 'observation from a standpoint of a third party', and it accepts only 'observation from a standpoint of the person concerned.' 'Observation from a standpoint of the person concerned' has two patterns. One of them is 'Subjective observation from a standpoint of the person concerned', which is an observation of observer about him/herself. The other is 'Objective observation from a standpoint of the person concerned', which is an observation of observer about other from a viewpoint of the person concerned.Now, with respect to the movement of light in a light clock, let us study the difference between 'observation from a standpoint of a third party' and 'observation from a standpoint of the person concerned.' Here, 'observation from a standpoint of a third party' looks like 'relativistic observasion', because it considers 'Lorentz contraction.'
There is a sphere with a radius of
 . Inside of the sphere is free space, and the inside of the wall of the sphere is made with mirror. Light is emitted from the center of the sphere, and then it spreads keeping shape of sphere. After it rebounds on the mirror, it deflates keeping shape of sphere, and then it calms down to the center of the sphere. Let us call the sphere 'light clock with a shape of sphere.' When the 1st observer, who is stationary relative to the light clock with a shape of sphere, paints locus of light of one cycle with yellow color, a yellow sphere is painted. When the 2nd observer traveling with linear uniform motion at a speed of
. Inside of the sphere is free space, and the inside of the wall of the sphere is made with mirror. Light is emitted from the center of the sphere, and then it spreads keeping shape of sphere. After it rebounds on the mirror, it deflates keeping shape of sphere, and then it calms down to the center of the sphere. Let us call the sphere 'light clock with a shape of sphere.' When the 1st observer, who is stationary relative to the light clock with a shape of sphere, paints locus of light of one cycle with yellow color, a yellow sphere is painted. When the 2nd observer traveling with linear uniform motion at a speed of  relative to the 1st observer paints locus of light of one cycle with yellow color, a yellow elliptic sphere, which longer axis is in the moving direction, is painted. The space point on which light is emitted and the space point on which light calms down are focuses of the yellow elliptic sphere.
relative to the 1st observer paints locus of light of one cycle with yellow color, a yellow elliptic sphere, which longer axis is in the moving direction, is painted. The space point on which light is emitted and the space point on which light calms down are focuses of the yellow elliptic sphere.Please notice two photons of the light in the light clock with a shape of sphere with respect to the 2nd observer. The photon A travels in the moving direction of the light clock with a shape of sphere, and then it collides with the point A on the mirror. The photon B travels in the perpendicular direction to the movement of the light clock with a shape of sphere with respect to the 1st observer, and then it collides with the point B on the mirror. Let us think about this situation.
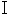

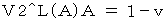
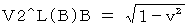

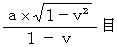
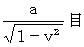

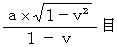
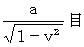

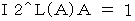
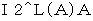 owing to the following
owing to the following 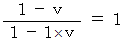
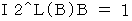

 .
. .
.
 .
. .
.'Lorentz transformation from the 2nd observer's coordinate system to the 1st observer's coordinate system' is a transformation from 'a subjective observation from a viewpoint of a third party about the 1st observer by the 2nd observer' to 'an objective observation from a viewpoint of the person concerned about the 1st observer by the 2nd observer'. It is not a transformation from 'a subjective observation from a viewpoint of a third party about the 1st observer by the 2nd observer' to 'a subjective observation from a viewpoint of the person concerned about the 1st observer by the 1st observer'. 'an objective observation from a viewpoint of the person concerned about the 1st observer by the 2nd observer' looks like 'a subjective observation from a viewpoint of the person concerned about the 1st observer by the 1st observer', but they are different. The former is done with a measure and a clock that the 1st observer is carrying in the 2nd observer's observation, the latter is done with a measure and a clock that the 1st observer is carrying in the 1st observer's observation, It is the purpose of this Lorentz transformation that we translate an observation of Newtonian mechanics into an observation of relativity on an observation about the same object by the same observer.
'Inverse Lorentz transformation from the 1st observer's coordinate system to the 2nd observer's coordinate system' is a transformation from 'an objective observation from a viewpoint of the person concerned about the 1st observer by the 2nd observer' to 'a subjective observation from a viewpoint of a third party about the 1st observer by the 2nd observer'. It is not a transformation from 'a subjective observation from a viewpoint of the person concerned about the 1st observer by the 1st observer' to 'a subjective observation from a viewpoint of a third party about the 1st observer by the 2nd observer'. It is the purpose of this Inverse Lorentz transformation that we translate an observation of relativity into an observation of Newtonian mechanics about one object by one observer.
Lorentz transformation is a coordinate conversion from a rectangular coordinate system to an oblique coordinate system. Inverse Lorentz transformation is a coordinate conversion from an oblique coordinate system to a rectangular coordinate system, because it is an inverse transformation of Lorentz transformation. A rectangular coordinate system shows 'a subjective observation from a viewpoint of a third party' on Newtonian mechanics, and an oblique coordinate system shows 'an objective observation from a viewpoint of the person concerned' on relativity. Figure 0901 in Chapter 9 shows 'an objective observation from a viewpoint of the person concerned', and Figure 0902 shows 'a subjective observation from a viewpoint of a third party.' So, in fact, Figure 0901 must be an oblique coordinate system.
(2)
The purpose of Michelson-Morley experiment is to proof the wind of ether. We consider that ether is traveling at a speed of
 relative to the experimental device. Time intervals for making a round trip of light in the direction of the wind of ether is different from time intervals for making a round trip of light in the direction perpendicular to the wind of ether. Let
relative to the experimental device. Time intervals for making a round trip of light in the direction of the wind of ether is different from time intervals for making a round trip of light in the direction perpendicular to the wind of ether. Let  be the speed of light under the situation without the wind of ether. Let
be the speed of light under the situation without the wind of ether. Let 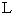
 be the distance btween the light source and the mirror. The expected value of time intervals for making a round trip of light is as follows :
be the distance btween the light source and the mirror. The expected value of time intervals for making a round trip of light is as follows : Time intervals for making a round trip of light in the direction perpendicular to the wind of ether
Time intervals for making a round trip of light in the direction perpendicular to the wind of ether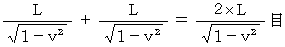
Because, both of the speed of going light and the speed of coming back light relative to the experimental device is
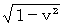 .
.  Time intervals for making a round trip of light in the direction of the wind of ether
Time intervals for making a round trip of light in the direction of the wind of ether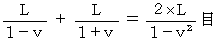
Because, the speed of going light relative to the experimental device is
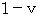 and the speed of coming back light is
and the speed of coming back light is 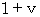 .
. be time intervals for light to go. Then, we obtain the
be time intervals for light to go. Then, we obtain the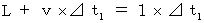
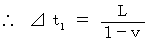
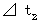 be time intervals for light to come back. Then, we obtain
be time intervals for light to come back. Then, we obtain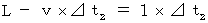
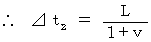
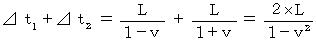
Contrary expectations, the result of Michelson-Morley experiment showed that
 is equal to
is equal to  . Then, I think that Lorentz and Einstein thought as follows :
. Then, I think that Lorentz and Einstein thought as follows :

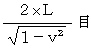 is right.
is right.
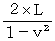 but
but 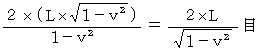 .
.
Let the 1st observer be a stationary observer relative to the pilot machine of Michelson-Morley Experiment. Let the 2nd observer be a traveling observer with the same velocity as the wind of ether relative to the 1st observer. The observation of the 1st observer before inverse Galilean transformation is 'a subjective observation from a viewpoint of the person concerned about the 1st observer by the 1st observer under the situation with the wind of ether.' The observation of the 2nd observer after inverse Galilean transformation is 'a subjective observation from a viewpoint of a third party about the 1st observer traveling under assumption that there is no relative wind of ether by the 2nd observer under the situation without the wind of ether.' The former seems to be a realistic observation. Michelson-Morley Experiment, however, denied it. Then, the latter must be a realistic observation. So, let us think about the coordinate system of the 2nd observer.
Note :![]() Inverse Galilean transformation makes the speed of light
Inverse Galilean transformation makes the speed of light  ,
,
![]() because it makes the wind of ether stop. Inverse Galilean
because it makes the wind of ether stop. Inverse Galilean
![]() transformation makes the distance between the light source
transformation makes the distance between the light source
![]() and the mirror not
and the mirror not 
 .
.

The speed of going light is equal to the speed of coming back light relative to the 1st observer; let
 be these speeds. Then, we obtain the following equality :
be these speeds. Then, we obtain the following equality :
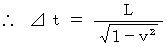
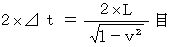

Time intervals is
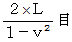 , because inverse Galilean transformation does not make time intervals change.
, because inverse Galilean transformation does not make time intervals change.It must be equal to the round trip time of light in the perpendicular direction relative to the wind of ether
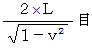 . Then,
. Then, 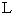 must become
must become 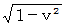 times larger. That is, the space of inertial frame of reference of the traveling 1st observer contracts in the direction of its motion.
times larger. That is, the space of inertial frame of reference of the traveling 1st observer contracts in the direction of its motion.Notes :
Inverse Galilean transformation of the motion of going light is as follows :
 .
.Space-time positional vector from the light source to the mirror in the 1st observer's observation :
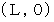
It is converted to the 2nd observer's coordinate system :
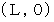
Space-time vector that shows movement of going light in the 1st observer's observation :
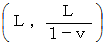
It is converted to the 2nd observer's coordinate system :
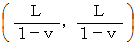
Galilean transformation works out the following composition of velocities :
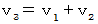
Galilean transformation is expressed as follows :
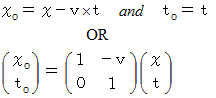
Lorentz's view is that there is the wind of ether and the space of the observer contracts from a viewpoint of the observer concered. Einstein's view is that there is no wind of ether and the space of the observed person contracts from a viewpoint of a third observer. We know that Lorentz's view is wrong and Einstein's view is right. However, Einstein's view at that time was based on Galilean transformation of Newtonian mechanics. Therefore, he needed 'Lorentz contraction' to make his explanation of the fact depending on 'Constancy of light speed', which denies Galilean transformation, consistent. We can say that Einstein at that time could deny the wind of ether, but he could not deny ether itself. The reason why is that we can not help abandoning Galilean transformation to deny ether itself and accept 'constancy of speed of light'. In those days, even Einstein had thought
 Observation is absolute and from the viewpoint of a third party. It must be done by comparing with something standard in common.
Observation is absolute and from the viewpoint of a third party. It must be done by comparing with something standard in common. He needed
He needed  Eye of God in windless space
Eye of God in windless space instead of the wind of ether. This view is different from his idea after he found that
instead of the wind of ether. This view is different from his idea after he found that  Observation is relative and from the viewpoint of the person concerned
Observation is relative and from the viewpoint of the person concerned
Lorentz contraction was a tool to translate into the observation of the theory of relativity from the observation of Newtonian mechanism at the dawn of the theory of relativity. After Einstein denied the either, the tool changed from Lorentz contraction to Lorentz transformation. Therefore, the concept of Lorentz contraction changed from 'Contraction of the observer's space' to 'Contraction of the observed traveling inertial frame or reference.
Today's theory of relativity considers Lorentz transformation as the tool of the relativistic coordinate conversion and the base of the theory of relativity. I, however, think it is not the tool of the relativistic coordinate conversion and it is a tool to translate into an objective observation from a viewpoint of the person concerned, i.e. the observation of the theory of relativity, from a subjective observation from a viewpoint of a third party, i.e. the observation of Newtonian mechanism. I think that Lorentz transformation is not the relativistic coordinate conversion which makes two observations of two observers correspond each other. Therefore, I think Lorentz contraction means the difference of space intervals between the observation of Newtonian mechanism and the observation of the theory of relativity, which observations belong to one observer. Plus, I think there is no difference of space intervals between two spaces of two observers.











Now, let us think about a light clock with Epstein's space-time. Let the mirror A and the mirror B be two mirrors of the light clock. In the coordinate system of the 1st observer, the mirror A keeps being on the space-time origin and the mirror B keeps being on the constant point on the X-axis. The 2nd observer is traveling in the negative direction on the X-axis at a speed of
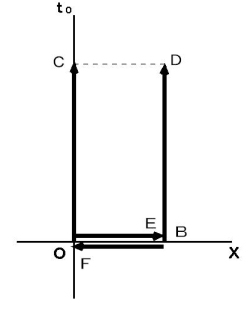
 . When the 2nd observer is on the space-time origin in the coordinate system of the 1st observer, the mirror A reflects light. Then light approaches the mirror B and the mirror B reflects light, and then light returns to the mirror A. I show this situation in the coordinate system of the 1st observer. Please see Figure 1202. We consider space is one-dimension to be simple. Figure 1202 shows Epstein's space-time.
. When the 2nd observer is on the space-time origin in the coordinate system of the 1st observer, the mirror A reflects light. Then light approaches the mirror B and the mirror B reflects light, and then light returns to the mirror A. I show this situation in the coordinate system of the 1st observer. Please see Figure 1202. We consider space is one-dimension to be simple. Figure 1202 shows Epstein's space-time.Figure 1202
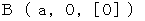
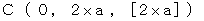

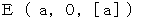
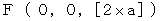
Next, I show this situation in the coordinate system of the 2nd observer. Please see Figure 1203. We obtain it by transforming Figure 1202 with inverse Lorentz transformation.
Figure 1203
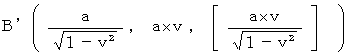

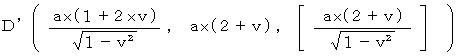
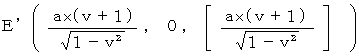
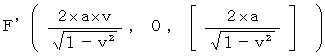
Owing to the value of absolute-time point of the space-time point

 and the space-time point
and the space-time point 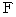
 , we see the light makes a round trip for
, we see the light makes a round trip for 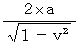 目 . Therefore, we see a light clock ticks away
目 . Therefore, we see a light clock ticks away times slowly than it stands still.
times slowly than it stands still.Owing to the above-mentioned consideration, we come to the conclusion as follows:
 Time passes
Time passes 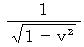 times slowly in an inertial frame of reference traveling at a speed of
times slowly in an inertial frame of reference traveling at a speed of  .
.
Therefore, 'contradiction of the theory of relativity; if you are, so am I' does not disappear by replacing Minkowsky space-time with Epstein's space-time.
(3)
There are four styles of observation.
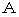 :
:Observation of a stationary object with a measure being carried by an observer
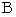 :
:Observation of a traveling object with a measure being carried by an observer
 :
:Observation of a looked-like-stationary object with a measure being carried by the object observed by an observer
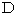 :
:Observation of a traveling object with a measure being carried by the object observed by an observer
I don't have described about
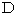 yet. So, I explain it. The example is as follows :
yet. So, I explain it. The example is as follows : Light and a rocket at a speed of light are emitted at the same time from the same space point to the stationary space point on which Mr. T exists. Ms. S is on the rocket. With respect to Mr. T, light and the rocket collide with Mr. T at the same time. With respect to Ms. S, however, light collides with Mr. T firstly and then the rocket collides with Mr. T secondly.
Light and a rocket at a speed of light are emitted at the same time from the same space point to the stationary space point on which Mr. T exists. Ms. S is on the rocket. With respect to Mr. T, light and the rocket collide with Mr. T at the same time. With respect to Ms. S, however, light collides with Mr. T firstly and then the rocket collides with Mr. T secondly.
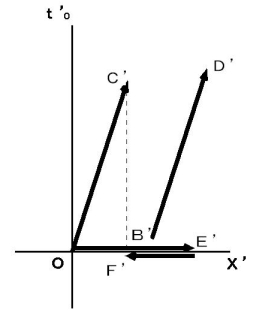
Above-mentioned observation about Mr. T by Ms. S is 'Objective observation from a standpoint of a third party' about Mr. T by Ms. B, time point of Mr. T observed by Ms. B is always
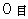 . Therefore, with respect to Ms. B, light and the rocket collide with Mr. T at the same time. Plus, light collides with Mr. T as soon as it is emitted; it is nonsense. Therefore, 'Objective observation from a standpoint of a third party' is not a realistic observation.
. Therefore, with respect to Ms. B, light and the rocket collide with Mr. T at the same time. Plus, light collides with Mr. T as soon as it is emitted; it is nonsense. Therefore, 'Objective observation from a standpoint of a third party' is not a realistic observation.It is rude to the theory of relativity that we take
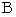 , which is an observation in Newtonian mechanics, into the theory of relativity to make same contradictions. However, the contradiction coming from
, which is an observation in Newtonian mechanics, into the theory of relativity to make same contradictions. However, the contradiction coming from 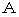 or
or  is the true contradiction of theory of relativity; it is 'contradiction of the theory of relativity; if you are, so am I'.
is the true contradiction of theory of relativity; it is 'contradiction of the theory of relativity; if you are, so am I'.The 2nd way to escape from a maze of paradox of the relativity is that we must throw out a standpoint of a third party and we must accept observations in the coordinate system of a person concerned; the person concerned stands still in his coordinate sytem.
When we think about following physical items, we tend to fall in a standpoint of a third party:
 collision of two objects
collision of two objects Simultaneity of two events, i.e. collision of an object and photon
Simultaneity of two events, i.e. collision of an object and photon Field of gravity, Electric field, and Magnetic field
Field of gravity, Electric field, and Magnetic field Velocity
Velocity Doppler's effect
Doppler's effectI think that relativistic observation is relative, subjective, and from a standpoint of the person concerned.
 Subjective observation
Subjective observation is done with a stationary scale and a stationary clock relative to the observer. In
is done with a stationary scale and a stationary clock relative to the observer. In  observation from a standpoint of the person concerned
observation from a standpoint of the person concerned , we consider a standard object of the observation stationary. Out of above-mentioned three styles of observation, only the style A is realistic. I think Lorentz transformation is a comparison of the identical object relative to the stationary observer between two observers traveling relatively. It is a relativistic way of thinking. It is not a relativistic way of thinking that we compare two observations of two relatively traveling observers with respect to different events of two objects, for example two observes each other. That is, relativity does not compare
, we consider a standard object of the observation stationary. Out of above-mentioned three styles of observation, only the style A is realistic. I think Lorentz transformation is a comparison of the identical object relative to the stationary observer between two observers traveling relatively. It is a relativistic way of thinking. It is not a relativistic way of thinking that we compare two observations of two relatively traveling observers with respect to different events of two objects, for example two observes each other. That is, relativity does not compare  B with respect to A
B with respect to A and
and  A with respect to B.
A with respect to B. But, the result coming from Lorentz transformation is the contradiction as
But, the result coming from Lorentz transformation is the contradiction as  If you are, so am I.
If you are, so am I. The contradiction is as follows :
The contradiction is as follows :
 The movement of
The movement of  with respect to
with respect to 
 is the same as
is the same as  the movement of
the movement of  with respect to
with respect to 
 Plus, it is
Plus, it is 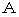
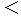
 with respect to
with respect to 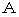 , and it is
, and it is 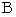
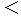
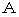 with respect to
with respect to 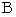 .
.
By the way, let us think about 'Inverse Lorentz transformation' through 'relativity of simultaneity.'
Please imagine; a train is passing the platform at high speed. There is Mr. B on the midpoint of the train. There is Mr. A on the platform. When they just pass each other, two flashes are emitted from a light source on the front of the train and a light source on the back of the train at the same time.
Question 1 :
Question 2 :

The coordinate system of the 1st observer, i.e. Mr. B, observed by the 2nd observer, i.e. Mr. A :

The event taking part in the 1st observer, i.e. Mr. B, in the coordinate system of the 2nd observer, i.e. Mr. A :
Therefore, in the observation of Mr. A, Mr. B sees simultaneously two flashes emitted at the same time.
( The relativistic observation before coordinate conversion is adopted.)

The coordinate system of the 1st observer, i.e. Mr. B :

The event taking part in the 1st observer, i.e. Mr. B, in the coordinate system of the 2nd observer, i.e. Mr. A :
Therefore, in the observation of Mr. A, Mr. B sees simultaneously two flashes emitted at different times.
( The observation of Newtonian mechanics after coordinate conversion is adopted.)
By the way, Mr. A is not absolutely standing still. The kinetic relationship of Mr. A and Mr. B is relative. Therefore, it is true that in the observation of Mr. A, he sees simultaneously two flashes emitted at the same time and in the observation of Mr. B, Mr. A sees simultaneously two flashes emitted at different times.

The coordinate system of the 1st observer, i.e. Mr. B :

The event taking part in the 1st observer, i.e. Mr. B, in the coordinate system of another 1st observer, i.e. Mr. A :
Therefore, in the observation of Mr. A, Mr. B sees two flashes emitted simultaneously at different times.
This misunderstanding is consequentially the same as the following misunderstanding of Newtonian mechanics. It is the reason why it is so that the one who misunderstands Lorentz transformation misunderstands as follows :
 Lorentz transformation shows the mapping between one subjective observation and another subjective observation.
Lorentz transformation shows the mapping between one subjective observation and another subjective observation.

The coordinate system of the 1st observer, i.e. Mr. B :

The event taking part in the 1st observer, i.e. Mr. B, in the coordinate system of another 1st observer, i.e. Mr. A :
Therefore, in the observation of Mr. A, Mr. B sees two flashes emitted simultaneously at different times.

The coordinate system of the 1st observer, i.e. Mr. B :

The event taking part in the 1st observer, i.e. Mr. B, in the coordinate system of another 1st observer, i.e. Mr. A :
Among, it is the same as Newtonian mechanics. From now, one who has not finished growing up to relativist tries to deny 'a subjective observation from a viewpoint of a third party' and tries to stand in the viewpoint of the person concerned, and then he corrects 'the observation of Mr. A about Mr. B from a viewpoint of a third party' as follows :
 In the observation of another 1st observer, i.e. Mr. A, the 1st observer, i.e. Mr. B, sees two flashes at different times. Now we warp to the coordinate system of the 1st observer, i.e. Mr. B. Then, in the coordinate system of the 1st observer, i.e. Mr. B, the distance between Mr. B and the light source on the front of the train is equal to the distance between Mr. B and the light source on the back of the train. Therefore, it is true that two flashes were emitted at different times.
In the observation of another 1st observer, i.e. Mr. A, the 1st observer, i.e. Mr. B, sees two flashes at different times. Now we warp to the coordinate system of the 1st observer, i.e. Mr. B. Then, in the coordinate system of the 1st observer, i.e. Mr. B, the distance between Mr. B and the light source on the front of the train is equal to the distance between Mr. B and the light source on the back of the train. Therefore, it is true that two flashes were emitted at different times.
Therefore, in the observation of Mr. A, Mr. B sees at different times two flashes emitted at different times.
(4) Proposal of the coordinate conversion which is a root of theory of Relativity
I propose the new coordinate conversion which can take place of Lorentz transformation. The different poits between it and Lorentz transformation are as follows :
I propose a new coordinate transformation which is the foundation of relativity. It is different in following respects from Lorenz transformation :



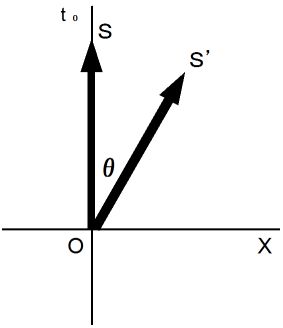
The new coordinate conversion is a linear conversion, and it keeps 'traveling intervals of an object through four-dimensional space time' constant. It converts a space-time point with rotation. To simplify, we consider three-dimensional space as one-dimension. The coordinate conversion, which rotates a space-time point with clockwise rotation, is expressed generally as follows :
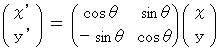
 (Expression 1201)
(Expression 1201)Therefore, we consider that my coordinate conversion from the 1st observer's coordinate system to the 2nd observer's coordinate system is expressed as follows :
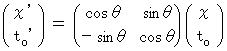
Please see Figure 1208. The vector
 showing the movement of an object through space-time is rotated with clockwise rotation at an angle of
showing the movement of an object through space-time is rotated with clockwise rotation at an angle of 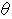 radian, and then it is converted to the vector
radian, and then it is converted to the vector  .
.Figure 1208

First, let us think about the basic conversion from the 0th observer to the 1st observer traveling at a speed of
 relative to the 0th observer. Please see Figure 1209.
relative to the 0th observer. Please see Figure 1209.Figure 1209
How is the coordinate conversion :
Relative-time intervals of an object are equal to Absolute-time intervals with respect to the 0th observer. Therefore, it is


 .
.Moreover, it is
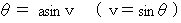 .
.So, we obtain the following expression :
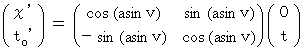
Therefore,
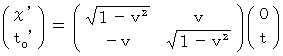
 (Expression 1202)
(Expression 1202)Therefore,
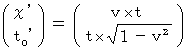
Next, let us think about the conversion from the 1st observer traveling at a speed of
 relative to the 0th observer to the 2nd observer traveling at a speed of
relative to the 0th observer to the 2nd observer traveling at a speed of 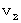 relative to the 1st observer.
relative to the 1st observer.For that purpose, we use the fact that the 2nd observer is originally the 1st observer. We obtain the speed of the 2nd observer relative to the 1st observer(
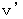 )with the relativistic composition of speeds as follows :
)with the relativistic composition of speeds as follows :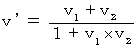
Therefore, the movement of the object with respect to the 2nd observer is expressed as follows :
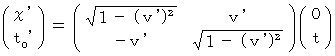
Therefore,
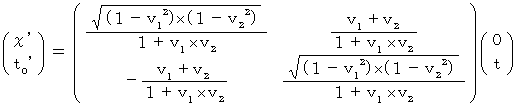
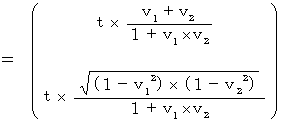
That's why we obtain the following expression showing the coordinate conversion from the 1st observer traveling at a speed of
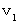 relative to an observed object to the 2nd observer traveling at a speed of
relative to an observed object to the 2nd observer traveling at a speed of 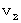 relative to the 1st observer :
relative to the 1st observer :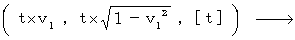
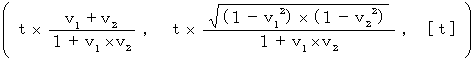
 (Expression 1203)
(Expression 1203)This expression is the root of 'Inertial System Theory of Relativity.' I call it 'Bioring's transformation.'
For example, the coordinate conversion of the space-time point on which an object traveling at a speed of
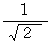 exists at a time point of
exists at a time point of  from the 1st observer to the 2nd observer traveling at a speed of
from the 1st observer to the 2nd observer traveling at a speed of  relative to the 1st observer is expressed as follows :
relative to the 1st observer is expressed as follows :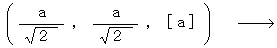
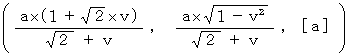
We can not express exactly an event from a standpoint of a third party, even if we use Bioring's transformation. This transformation can deal only with observers and observed objects, all of which pile up at the same time.
(6)
[ Inverse Lorentz transformation on space-time intervals from the 0th observer to the 1st observer ( The established theory ) ]
---- How does other people ( The observer B ) misobserve my avtion ( The observer A ) ? ----
 The action :
The action : Let time intervals while the action is observed by the observer A be
Let time intervals while the action is observed by the observer A be 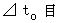 .
. Traveling space intervals
Traveling space intervals  of the heart while the action is observed by the observer A are as follows :
of the heart while the action is observed by the observer A are as follows :
 When the action is observed by the observer B on linear uniform motion at a speed of
When the action is observed by the observer B on linear uniform motion at a speed of  relative to the observer A, time intervals
relative to the observer A, time intervals 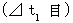 of the action observed by the observer B are as follow :
of the action observed by the observer B are as follow :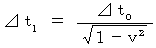
 Traveling space intervals
Traveling space intervals 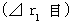 of the heart while the action is observed by the observer B are as follows :
of the heart while the action is observed by the observer B are as follows :
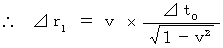
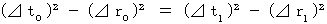
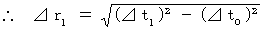
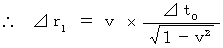
[ Bioring's transformation on space-time intervals from the 0th observer to the 1st observer ]
---- Other people ( The observer B ) is observing my action ( The observer A ) as it is. ----
 The action :
The action : Let absolute-time intervals while the action is observed by the observer A be
Let absolute-time intervals while the action is observed by the observer A be 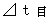 .
. Traveling space intervals
Traveling space intervals 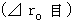 of the heart while the action is observed by the observer A are as follows :
of the heart while the action is observed by the observer A are as follows :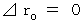
 Traveling relative-time intervals
Traveling relative-time intervals 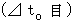 of the heart while the action is observed by the observer A are as follows :
of the heart while the action is observed by the observer A are as follows :
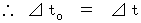
 When the action is observed by the observer B on linear uniform motion at a speed of
When the action is observed by the observer B on linear uniform motion at a speed of  relative to the observer A, absolute-time intervals while the action is observed by the observer B are
relative to the observer A, absolute-time intervals while the action is observed by the observer B are 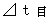 . Because, absolute-time intervals are constant regardless of a coordinate conversion.
. Because, absolute-time intervals are constant regardless of a coordinate conversion. Traveling space intervals
Traveling space intervals 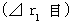 of the heart while the action is observed by the observer B are as follows :
of the heart while the action is observed by the observer B are as follows :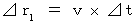
 Traveling relative-time intervals (
Traveling relative-time intervals (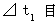 ) of the heart while the action is observed by the observer B are as follows :
) of the heart while the action is observed by the observer B are as follows :
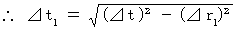
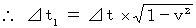
[ Lorentz transformation on space-time intervals from the 1st observer to the 0th observer ( The established theory ) ]
---- What is the truth of an action of other people misobserved by me ( The observer B ) ? ----

 relative to the observer B beats once.
relative to the observer B beats once.
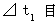 .
.
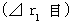 of the heart while the action is observed by the observer B are as follows :
of the heart while the action is observed by the observer B are as follows :

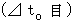 of the action observed by the observer A are as follow :
of the action observed by the observer A are as follow :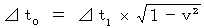
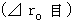 of the heart while the action is observed by the observer A are as follows :
of the heart while the action is observed by the observer A are as follows :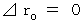
 Let us make sure that proper time intervals are constant regardless of a coordinate conversion.
Let us make sure that proper time intervals are constant regardless of a coordinate conversion.
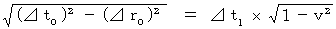
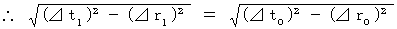
[ Bioring's transformation on space-time intervals from the 1st observer to the 0th observer ]
---- I ( The observer B ) am observing an action of other people as it is. ----
 The action :
The action : relative to the observer B beats once.
relative to the observer B beats once. Let absolute-time intervals while the action is observed by the observer B be
Let absolute-time intervals while the action is observed by the observer B be 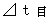 .
. Traveling space intervals
Traveling space intervals 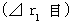 of the heart while the action is observed by the observer B are as follows :
of the heart while the action is observed by the observer B are as follows :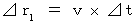
 Traveling relative-time intervals (
Traveling relative-time intervals (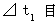 ) of the heart while the action is observed by the observer B are as follows :
) of the heart while the action is observed by the observer B are as follows :
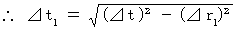
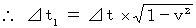
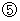 When the action is observed by the stationary observer A relative to the heart, absolute-time intervals while the action is observed by the observer A are
When the action is observed by the stationary observer A relative to the heart, absolute-time intervals while the action is observed by the observer A are  . Because, absolute-time intervals are constant regardless of a coordinate conversion.
. Because, absolute-time intervals are constant regardless of a coordinate conversion. Traveling space intervals
Traveling space intervals 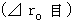 of the heart while the action is observed by the observer A are as follows:
of the heart while the action is observed by the observer A are as follows: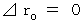
 Traveling relative-time intervals
Traveling relative-time intervals 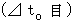 of the heart while the action is observed by the observer A are as follows:
of the heart while the action is observed by the observer A are as follows:
A State of Relativity
I am only one in the world. But, there are a lot of I; the number of I is equal to the number of observers.
I want to be observed as this. But my hope is not realized. Because an observer must decide how to observe me.
All observers, however, come home every year to conglaturate me just on my birthday without coming on other days.
There am I observing me. There am I observed by me. These I am identical. There am I observed by you. This I am different from those I. I observed by me and you observed by you are standing still and traveling in the direction of the time axis. If we pile up I observed by me and you observed by you, something hiding appears.
You say as follows :
 It is interesting. Time point when I received a Christmas card from you. Time point when I sent a birthday card for you. These time points are real for me. But, these time points are illusion for you. The color which you recognize as blue might be the color which I recognize as red.
It is interesting. Time point when I received a Christmas card from you. Time point when I sent a birthday card for you. These time points are real for me. But, these time points are illusion for you. The color which you recognize as blue might be the color which I recognize as red.
It is very lonly. So, I see from your standpoint.
The object A is only one, but there are many objects A, the same as the number of observers.
The object A is being observed by many observers traveling through space in various directions. Let's suppose they are on the same space-time point as the object A when they start observation. The object A is fixed on a certain point which is going away through four-dimensional space-time from the origin at the speed of light.
When we think about a coordinate conversion from one observer to another on the movement of the object A , we consider that all observers keep being on the same point while they observe the object A ; the point on which all observers exsit is traveling on the relative-time axis at the speed of light while keeping their consciousnesses on the space-time origin.
Many points, on which object A is fixed, are going away through four-dimensional space-time from the origin in various directions at the speed of light relative to all observers.
A light emitted in an instant from a source of light is only one in the world. It appears with the same apperance for all observers.
Considering space to be two-dimensions, let us imagine a light emitted in an instant from a source of light. There are many observers traveling at different speeds in different directions. All of them are on the same point traveling on the relative-time axis, which is perpendicular to the space plane. The point travels from the space-time origin at a speed of light. Their consciousnesses stay on the space-time origin. For all observers, traveling of the light is expressed as circle spreading on the space plane from the space-time origin at a speed of light.