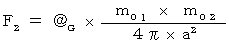Chapter 13 Change of Frequency of Light due to Movement of a Light Source
Change of Frequency of Light due to Movement of a Light Source
Figure 1301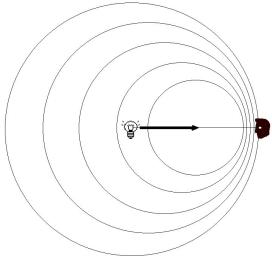
Let
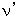 be a frequency of light emitted from a light source traveling at a speed of
be a frequency of light emitted from a light source traveling at a speed of  .
.Let
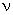 be a frequency of light emitted from a stationary light source.
be a frequency of light emitted from a stationary light source.Then,
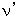 is expressed as follows:
is expressed as follows: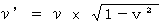
 (Equality 13-1)
(Equality 13-1)In fact, however, it is not just like so unless the light source is traveling in the perpendicular direction to the direction of the light source with respect to an observer, because it goes through 'Doppler effect.'
Let us think about the case, as Figure 1301, a light source is approaching the observer at a speed of
 . The light source is approaching the observer space intervals of
. The light source is approaching the observer space intervals of 
 per absolute-time interval of
per absolute-time interval of  . Therefore, due to 'Doppler effect,' the observed frequency of light (
. Therefore, due to 'Doppler effect,' the observed frequency of light ( 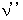 ) is
) is 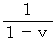 times much as
times much as 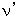 as follows:
as follows: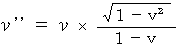
Therefore,
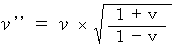
 (Equality 13-2)
(Equality 13-2)When the light source is going away from the observer at a speed of
 , what is the value of
, what is the value of 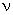 '' ? We can obtain the answer easily, because we only have to replace
'' ? We can obtain the answer easily, because we only have to replace  of (Equality 13-2) with
of (Equality 13-2) with 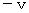 . Therefore, it is as foolows:
. Therefore, it is as foolows: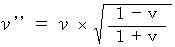
* Note :
When we think about a wave, which transmits through a medium, like the sounds, we must consider kinetic relationships between a source of a wave, a medium, and an observer.
For example :
Let
 be speed of the sounds.
be speed of the sounds.Let
 be relative speed between a sound source and an observer.
be relative speed between a sound source and an observer. When a stationary sound source starts approaching an observer, while the observer keeps still,
When a stationary sound source starts approaching an observer, while the observer keeps still,
 When a stationary observer starts approaching a sound source, while the sound source keeps still,
When a stationary observer starts approaching a sound source, while the sound source keeps still,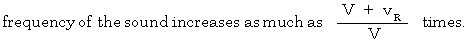
Chapter 14 Three Axioms and One Theorem
Three Axioms and One Theorem
 :
: :
: following time ( absolute-time )
following time ( absolute-time ) :
: :
: On one hand, it is defined that a number of vibrations of
On one hand, it is defined that a number of vibrations of
Now, I will explain the Theorem
 . This theorem is expressed as following equations:
. This theorem is expressed as following equations:Let
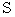 be a number of vibrations of a graviton for absolute-time intervals of
be a number of vibrations of a graviton for absolute-time intervals of 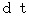 .
.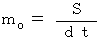 ,
, 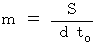
Therefore,
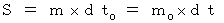
 (Equality 14-1)
(Equality 14-1)Moreover, please remember the next equality setting
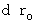


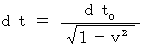
 (Equality 5-3)
(Equality 5-3)Therefore, the following equality is obtained from above two equalitys.
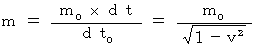
 (Equality 14-2)
(Equality 14-2)In my theory of relativity, the relationship between mass and rest mass is based on their definition.
Chapter 15 Momentum of Four-Dimensional Space-Time
Momentum of Four-Dimensional Space-Time
![]()
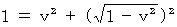
By multiplying both sides of this equality by mass squared, we obtain the next equality.
![]()
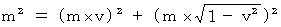
![]()
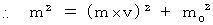
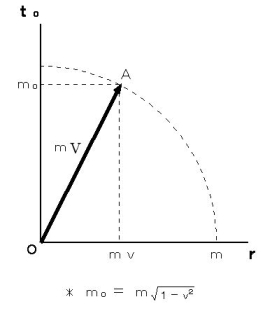
When we show this equality with the 'Epstein's four-dimensional space-time coordinate,' we see its meaning. Please see Figure 1502.
Fig.1502
![]()
![]() *
*![]() Four-dimensional space-time velocity :
Four-dimensional space-time velocity :
![]()
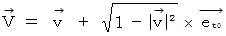
![]() Space velocity :
Space velocity :
![]()
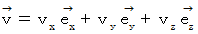
![]() Reltive-time velocity :
Reltive-time velocity :
![]()
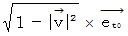
![]() Magnitude of four-dimensional space-time velocity :
Magnitude of four-dimensional space-time velocity :
![]()
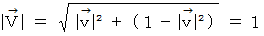
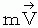 is the vector obtained by multiplying the 'four-dimensional space-time velocity' by mass of the object. The magnitude of 'four-dimensional space-time velocity' of any substace is
is the vector obtained by multiplying the 'four-dimensional space-time velocity' by mass of the object. The magnitude of 'four-dimensional space-time velocity' of any substace is  .
.
I call  'four-dimensional space-time momentum.' I call the space axes components of four-dimensional space-time momentum (
'four-dimensional space-time momentum.' I call the space axes components of four-dimensional space-time momentum ( 
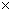
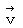 ) 'space momentum', and I call the relative-time axis component of four-dimensional space-time momentum
) 'space momentum', and I call the relative-time axis component of four-dimensional space-time momentum 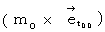 'relative-time momentum.'
'relative-time momentum.'
The magnitude of the relative-time momentum of an object is the same as 'rest mass' of the object.
The magnitude of the 'four-dimensional space-time momentum' of an object is the same as 'mass' of the object. Moreover, the unit of the four-dimensional space-time momentum is the same as that of massG it is '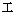 '.
'.
Let 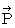 be a 'four-dimensional space-time momentum' of an object.
be a 'four-dimensional space-time momentum' of an object.
The following equation is valied:
![]()
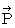

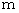
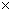
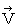
![]()
 (Equality 15-4)
(Equality 15-4)
![]()
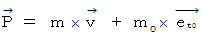
![]() b
b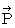 b
b 
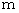
![]()
 (Equality 15-5)
(Equality 15-5)
I present following equalities related to these equalities:
![]()
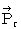

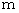
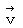
![]()
 (Equality 15-6)
(Equality 15-6)
![]()
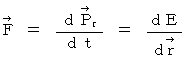
![]()
 (Equality 15-7)
(Equality 15-7)
![]() Note:
Note:![]() Let
Let 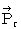 be 'space momentum.'
be 'space momentum.'
Chapter 16 What is Mass?
What is Mass?
I will prove 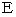

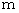 ; of coarse, it is promise to use
; of coarse, it is promise to use 
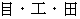 system of unit.
system of unit.
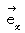 a unit vector of the X-axis.
a unit vector of the X-axis.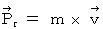 , we obtain the following
, we obtain the following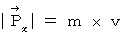
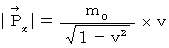
 (Equality 16-1)
(Equality 16-1)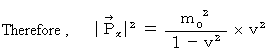
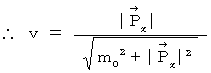
 (Equality 16-2)
(Equality 16-2)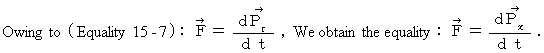
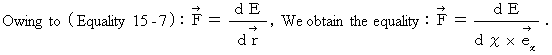
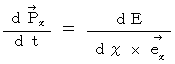
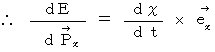
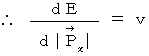
 (Equality 16-3)
(Equality 16-3)
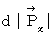 , we obtain the following expression :
, we obtain the following expression :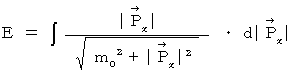
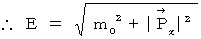
 (Equality 16-4)
(Equality 16-4)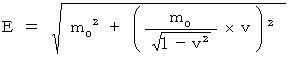
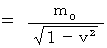
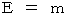
Therefore, we see that mass shows energy of an object.
{ Omission }
Please remember two kindergarteners mentioned in Chapter 2. I present an important point in that passage with following different expression:
 Please regard
Please regard  the measured number of spins of an object per unit modified relative-time interval
the measured number of spins of an object per unit modified relative-time interval as
as  the measured mass of the object.
the measured mass of the object. In fact, mass shows the amount of total energy of an object.
In fact, mass shows the amount of total energy of an object.
What does
 the measured number of spins of an object per unit modified relative-time interval
the measured number of spins of an object per unit modified relative-time interval mean? The answer is found in the Theorem
mean? The answer is found in the Theorem  stated in Chapter 14.
stated in Chapter 14.Vibrations of a graviton bear mass of an object, and they transmit gravitational field through space at the speed of light. As the 'anglar frequency (
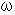 ) ' of a photon traveling through space shows energy, the 'frequency of a graviton' traveling through space shows 'rest energy (
) ' of a photon traveling through space shows energy, the 'frequency of a graviton' traveling through space shows 'rest energy (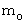 ) ' of the object.
) ' of the object.I call the following statement 'Law of vibration of graviton.':
 A number of vibrations of graviton in an object per unit absolute-time interval, in other words, frequency of graviton, i.e. 'rest mass', is constant, even if any observer traveling with linear uniform motion observes it. Vibration of raviton is compressed in only the relative-time direction, and then it travel through space at the speed of light. They produce gravitational field.
A number of vibrations of graviton in an object per unit absolute-time interval, in other words, frequency of graviton, i.e. 'rest mass', is constant, even if any observer traveling with linear uniform motion observes it. Vibration of raviton is compressed in only the relative-time direction, and then it travel through space at the speed of light. They produce gravitational field.
Chapter 17 Increase of Rest Mass as a result of Perfectly Inelastici Collision
Increase of Rest Mass as a result of Perfectly Inelastici Collision
In this chapter, we will study the following statement:
 Although the 'law of conservation of momentum' and the 'law of conservation of energy' holds good, the 'law of conservation of rest mass' does not hold good.
Although the 'law of conservation of momentum' and the 'law of conservation of energy' holds good, the 'law of conservation of rest mass' does not hold good.
Please imagineG two balls, one of them is black and another is white, with the same 'rest mass' of 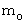 are approaching you at the same speed of
are approaching you at the same speed of  from left and right-hand sides.
from left and right-hand sides.
Therefore, the mass (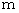 ) of these balls is as follows:
) of these balls is as follows:
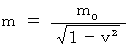
 (Equality 17-1)
(Equality 17-1)Immediately after that, two balls have collided head-on perfect inelastically under your very nose, and then they stuck and stopped in an instant.
Let
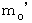 be rest mass of the stuck balls.
be rest mass of the stuck balls.Now, I will show you that
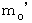 is not equal to twice of
is not equal to twice of 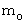 .
.First, we check the 'law of conservation of momentum.'
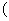
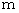
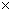

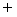
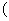
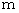
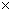
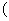
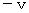


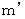
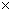



Second, we check the 'law of conservation of energy.'
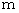
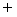
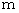

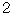
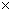
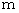
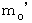
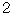
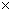
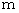

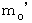
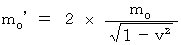
 (Equality 17-2)
(Equality 17-2)Now, let us consider how this situation is observed by your friend traveling with the same velocity as white-colored ball. Please see Figure 1701.
Figure 1701
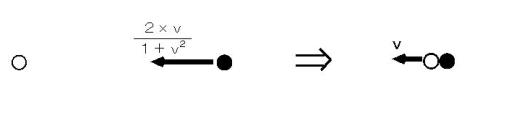
First, let us check the 'law of conservation of momentum.'
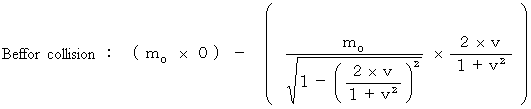
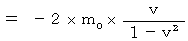

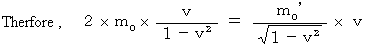

 (Equality 17-3)
(Equality 17-3){ Omission }
(Equality 17-2), (Equality 17-3), and (Equality 17-4) are the same form.
Therefore, in orde to both the 'law of conservation of momentum' and the 'law of conservation of energy' holds good, we must recognize that these equalities are right.
Owing to these equalities, we obtain
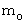


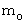 .
.Therefore, we see that rest mass, i.e. rest energy, increases as a result of a perfectly inelastic collision.
Chapter 18 Movement of an Object and Gravitational Field
Movement of an Object and Gravitational Field
Newton's law of universal gravitation is expressed with 
 system of units
system of units as follows:
as follows:
 (Equality 18-1)
(Equality 18-1)
The gravitational field does not instantaneously transmit through the space, but transmits at the speed of light. Therefore, the space intervals ( r ) of ( Equality 18-1 ) are correctly equivalent to space intervals through witch graviton emitted from the object A reaches the object B .
I described
 Law of vibrations of graviton
Law of vibrations of graviton  in Chapter 16. It is as follows:
in Chapter 16. It is as follows: A number of vibrations of a graviton in an object per unit absolute-time interval, in other words, a frequency of a graviton, i.e. 'rest mass', is constant, even if any observer traveling with linear uniform motion observes it. Vibrations of a graviton are compressed in only the relative-time direction, and then they travel through space at the speed of light. They produce gravity.
A number of vibrations of a graviton in an object per unit absolute-time interval, in other words, a frequency of a graviton, i.e. 'rest mass', is constant, even if any observer traveling with linear uniform motion observes it. Vibrations of a graviton are compressed in only the relative-time direction, and then they travel through space at the speed of light. They produce gravity.
'Vibrations of a graviton are compressed in only the relative-time direction' is equivarent to mass.
Let us study gravitational force exerting an influence on a traveling object. Please imagine. The object A and the object B are traveling with linear uniform motion on the same line with different velocity. Distance between them is getting long. There is an observer traveling with linear uniform motion on the line. There are three cases how the observer observs two objects.
Case 1:
When an observer is traveling with different velocity from them, both the object A and the object B are traveling with linear uniform motion.
Case 2:
When an observer is traveling with the same velocity as the object A , the object A keeps still and the object B are traveling with linear uniform motion.
Case 3:
When an observer is traveling with the same velocity as the object B , the object A are traveling with linear uniform motion and the object B keeps still.
Case 1 , Case 2 , and Case 3 are the identical form on the kinetic relationship between the object A and the object B . That is, we can not make a distinction between three cases on the kinetic relationship of two objects.
I call
 the identical form on the kinetic relationship
the identical form on the kinetic relationship
 kinetic identical form.
kinetic identical form.
Well, let us find how much is the object A's gravitational force exerting an influence on the object B.
Let
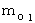 and
and 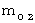 be rest mass of the object A and the object B , respectively.
be rest mass of the object A and the object B , respectively.Let
 be a speed of the object B relative to the object A .
be a speed of the object B relative to the object A .Then, speed of the object A relative to the object B is
 , and velocity of the object A relative to the object B is
, and velocity of the object A relative to the object B is 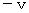 .
.Let
 be the distance of them when a graviton is emitted from the object B .
be the distance of them when a graviton is emitted from the object B .First, please see Figure 1801 showing Case 3 .
Figure 1801
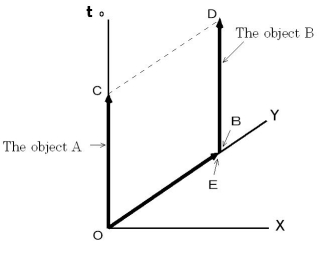
Owing to (Equality 18-1), the magnitude of the object A's gravitational force (
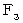 ) exerting an influence on the object B on the observation of an observer traveling with the same velocity as the object B is as follows:
) exerting an influence on the object B on the observation of an observer traveling with the same velocity as the object B is as follows: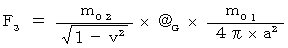
 (Equality 18-2)
(Equality 18-2)Second, please see Figure 1802. It shows Case 2 .
Figure 1802
The magnitude of the object A's gravitational force (
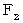 ) exerting an influence on the object B on the observation of an observer traveling with the same velocity as the object A may be as follows:
) exerting an influence on the object B on the observation of an observer traveling with the same velocity as the object A may be as follows:

 (Equality 18-3)
(Equality 18-3)(Equality 18-3) is wrong. We want to find how much the gravitational force exerting an influence on the object B is. So, we must take the standpoint of the person concerned, or the object B . Because, if we take the standpoint of the third party, speed of graviton may be more or less than the speed of light. In Case 3 , speed of graviton relative to the object B on the observation of the 1st observer is
 . In Case 2 , speed of graviton relative to the object B on the observation of the 1st observer is
. In Case 2 , speed of graviton relative to the object B on the observation of the 1st observer is 
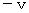 . Of course, speed of graviton relative to the person concerned is as follows :
. Of course, speed of graviton relative to the person concerned is as follows :
Therefore, if we want to find
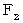 in Case 2, we must find
in Case 2, we must find 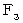 firstly, and then we must declare as follows:
firstly, and then we must declare as follows:
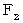 is equal to
is equal to 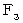 , because Case 2 is kinetic identical form as Case 3 .
, because Case 2 is kinetic identical form as Case 3 .
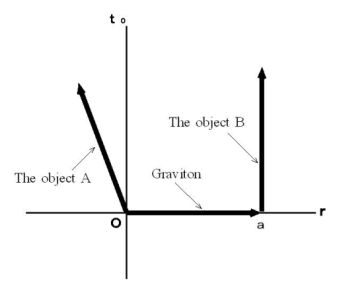
Next, we consider how much is the gravitational force for an observer traveling with linear uniform motion in the perpendicular direction to the line which connects the object A and the object B .
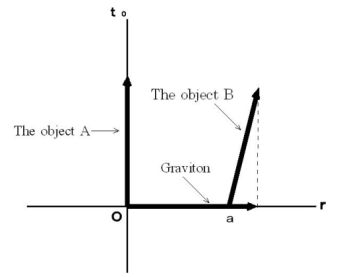
Please see Figure 1803. This figure shows the 1st observer's coordinate system. It shows that a graviton, which is emitted from the object A when the object A just existed on the origin, reaches the object B . To simplyfy, three-dimensional space is expressed with two-dimensions. The distance of the object A and B is
 , and they keep still.
, and they keep still.Figure 1803

The magnitude of the object A's gravitational force (
 ) exerting influence on the object B on the 1st observer's observation is as follows :
) exerting influence on the object B on the 1st observer's observation is as follows :
 (Equality 18-4)
(Equality 18-4)How does the 2nd observer traveling in the negative X-axis direction at a speed of
 observe this situation? We can obtain the 2nd obserever's coordinate system owing to (Expression 8-5) and (Expression 8-6) . Please see Figure 1804.
observe this situation? We can obtain the 2nd obserever's coordinate system owing to (Expression 8-5) and (Expression 8-6) . Please see Figure 1804.Figure 1804
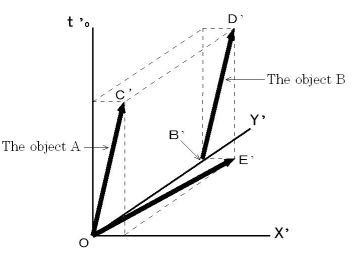
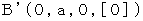
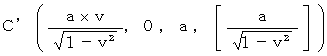
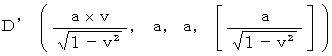
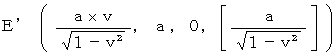
How much is the magnitude of the object A's gravitational force (
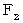 ) exerting an influence on the object B on the observation of the 2nd observer ?
) exerting an influence on the object B on the observation of the 2nd observer ?The situation of this question is silmilar to the above-mentioned question. The speed of graviton relative to the object B on the 2nd obderver's observation is not
 . That is, the magnitude of a third party's relative velocity of graviton relative to the traveling 1st observer from a viewpoint of the 2nd observer is
. That is, the magnitude of a third party's relative velocity of graviton relative to the traveling 1st observer from a viewpoint of the 2nd observer is 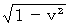 , and its direction is the Y-axis direction. Moreover, Figure 1804 shows a virtual space-time which deviates from the expanding four-dimensional space-time. So, to find
, and its direction is the Y-axis direction. Moreover, Figure 1804 shows a virtual space-time which deviates from the expanding four-dimensional space-time. So, to find 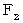 , firstly we must find a coordinate system, which is kinetic identical form as Figure 1804, and in which the object B keeps still. The 1st observer's coordinate system in Figure 1803 is kinetic identical form as the 2nd observer's coordinate system in Figure 1804. Therefore,
, firstly we must find a coordinate system, which is kinetic identical form as Figure 1804, and in which the object B keeps still. The 1st observer's coordinate system in Figure 1803 is kinetic identical form as the 2nd observer's coordinate system in Figure 1804. Therefore, 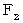

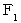 . So, owing to (Equality 18-4) ,
. So, owing to (Equality 18-4) , 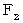 is as follows :
is as follows :