第11章 運動している物は時間が遅れ空間が縮む?
この章では、次の相対性理論の常識に挑戦します。
 移動する物質は時間が遅く進み、 光速になると時間が止まる。
移動する物質は時間が遅く進み、 光速になると時間が止まる。 移動する物質は運動方向に縮み、 光速になると厚みがなくなる。
移動する物質は運動方向に縮み、 光速になると厚みがなくなる。 もし彼が光の速さで移動するなら、 その間、 彼は活動を停止するので、 1
もし彼が光の速さで移動するなら、 その間、 彼は活動を停止するので、 1年後に、 1 光年離れた場所に、 彼は今の年齢のまま存在する。
 もし私たちが光の速さで移動するなら、 その間、 私たちは活動を停止する
もし私たちが光の速さで移動するなら、 その間、 私たちは活動を停止するので、 1 光年離れた場所の 1 年先の未来へ、 主観的に瞬間移動すること
ができる。
 未来へのタイムトラベルは可能である。 そのイメージは、「 双子のパラドッ
未来へのタイムトラベルは可能である。 そのイメージは、「 双子のパラドックス 」や 映画「 猿の惑星 」や お伽話「 浦島太郎 」の中にある。
* コメント :
さすがに
 は、 だれの目にも間違っていることがすぐにわかる
は、 だれの目にも間違っていることがすぐにわかると思うのですが、 これが正しいと錯覚してしまうことがあります。
 は、
は、  の「 彼 」を「 私たち 」に置き換えただけのように
の「 彼 」を「 私たち 」に置き換えただけのように思いますが、 そうではありません。 もし、 置き換えるのなら、 次の
ようにしなければなりません。
「 もし私たちが彼に対して光の速さで移動するなら、 彼に
とっては、 その間、 私たちは活動を停止するので、 彼に
とっては、 私たちは、 1 年後に、 1 光年離れた場所に、
今の年齢のまま存在する。」
移動は相対的な現象ですので、 観察者と被観察物質を入れ替
えても、 同様のことが言えます。 このとき、 矛盾が生じます。 相手
のケーキのほうがお互いに大きく見えるというような心理学で片づ
けることのできない矛盾です。 これらは、「 相対性理論のパラドッ
クス 」と言われます。
(1)「 ローレンツ収縮 」と「 移動する時計の遅れ 」に関する定説と珍解釈の紹介
 微小時空間の逆ローレンツ変換
微小時空間の逆ローレンツ変換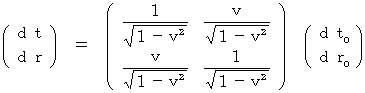
・・・・・・・・(式 11-1)
つまり、
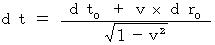 ・・・・・・(式 11-2)
・・・・・・(式 11-2)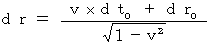 ・・・・・・(式 11-3)
・・・・・・(式 11-3)dt0 = 0 のとき、(式 11-3)より、
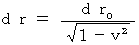 ・・・・(式 11-4)
・・・・(式 11-4)dr0 = 0 のとき、(式 11-2)より、
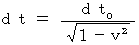 ・・・・(式 11-5)
・・・・(式 11-5) 微小時空間のローレンツ変換
微小時空間のローレンツ変換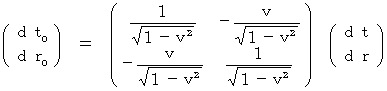
・・・・・・・・(式 11-6)
つまり、
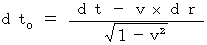 ・・・・・・(式 11-7)
・・・・・・(式 11-7)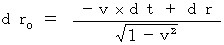 ・・・・・・(式 11-8)
・・・・・・(式 11-8)dt = 0 のとき、(式 11-8)より、
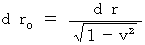 ・・・・・(式 11-9)
・・・・・(式 11-9)dr0 = 0 のとき、(式 11-8)より、
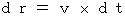
よって、(式 11-7)より、
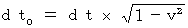 ・・・・(式 11-10)
・・・・(式 11-10) 「 移動している物体は収縮する( ローレンツ収縮 )」
「 移動している物体は収縮する( ローレンツ収縮 )」a)定説
静止している rt 系 にて、 同時点で、 移動している棒の両端の空点を調べる。
その距離が ⊿r であったとする。
微小時空間のローレンツ変換に属する(式 11-9)より、
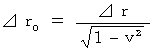
∴ 物体が静止すると伸展する。
↓↓
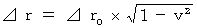
∴ 移動している物体は収縮する。
∴ 移動している物差しは収縮する。
b)珍解釈
移動している r0t0 系 にて、 同時刻に、 静止している棒の両端の位置を調べる。
その距離が ⊿r0 であったとする。
微小時空間の逆ローレンツ変換に属する(式 11-4)より、
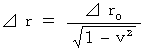
∴ 物体が移動し始めると伸展する。
∴ 移動している物体は伸展する。
∴ 移動している物差しは伸展する。
 「 移動している時計は遅れる( 移動している物質の活動はスロー )」
「 移動している時計は遅れる( 移動している物質の活動はスロー )」a)定説
移動している r0t0 系 にて、 静止している心臓が1回拍動するのに ⊿t0 が経過し
たとする。
微小時空間のローレンツ変換 に属する(式 11-10)より、
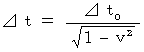
∴ 心臓が移動し始めると、 拍動にかかる時間が長くなる。
∴ 移動している心臓は、 ゆっくりと拍動する。
∴ 移動している物質の活動はスロー。
∴ 移動している時計はゆっくりと時を刻む
b)珍解釈
移動している r0t0 系 にて、 静止している時計の針が ⊿t0 経過したとする。
微小時空間の逆ローレンツ変換 に属する(式 11-5)より、
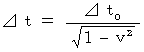
∴ 時計が移動し始めると、 いままでよりも多くの時間が経過する。
∴ 移動している時計は、 速く時を刻む。
∴ 移動している物質の活動はクイック。
* この珍解釈は滑稽すぎて、 私でさえも、「 いかがなものか 」と思いま
す。 そこで、「 座標変換によって、 観察時間が長くなる。」という考え方は
いかがでしょうか?
c)珍解釈その2
静止している rt 系 にて、 同空点で、 移動している糸電話の両端の時点を調べる。
静止している rt 系 にて、 糸電話が速さ
 で等速直線運動している。 その糸電話は糸を
で等速直線運動している。 その糸電話は糸をピンと張っており、 音声を速さ
 で伝える。 空間原点を音声入力側の一端が通過する瞬間
で伝える。 空間原点を音声入力側の一端が通過する瞬間に音声を入力し、 それから ⊿t の時間後に、 空間原点( 同一場所 )を音声出力側の他
端が通過する瞬間にその音声を出力する。
 のとき、 微小時空間のローレンツ変換に属する(式 11-7)より、
のとき、 微小時空間のローレンツ変換に属する(式 11-7)より、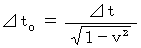
∴ 移動していた糸電話が静止すると、音声伝達にかかる時間が長くなる。
↓↓
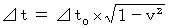
∴ 静止していた糸電話が移動し始めると、音声を短時間で伝達するようになる。
∴ 移動している物質の活動はクイック。
∴ 移動している時計は速く時を刻む。
 矛盾点のポイント
矛盾点のポイント1.
 の a) と
の a) と  の b) とを 比較してみてください。
の b) とを 比較してみてください。2.
 の a) と
の a) と  の b) とを 比較してみてください。
の b) とを 比較してみてください。3.
 の b) と
の b) と  の b) とを 比較してみてください。
の b) とを 比較してみてください。4.
 の a) と
の a) と  の a) とを 比較してみてください。
の a) とを 比較してみてください。5.
 の a) と
の a) と  の c) とを 比較してみてください。
の c) とを 比較してみてください。私が「 時 が伸びる 」と言うときは、 時 の経過のスピードが遅くなることを意味します。 一方、「 時間が長くなる 」と言うときは、 事象Aが起こった時刻 と 事象Bが起こった時刻 との間隔が長くなるということで、 時 の経過のスピードを表しているのではありません。 移動している慣性系は、 時 が伸びて、 観察者系の経過時間当たりの被観察系の経過時間 は 1 より小さくなっています。 このことをイメージするには、 両端を軽く引っ張って適度に伸ばしたゴム紐に1cm間隔で目盛りを書いた後、 そのゴム紐を縮めたり伸ばしたりして、実際の30cmに何個の目盛りが入っているかを数えてみてください。 ゴム紐が縮むと目盛りの数は増え、 ゴム紐が伸びると目盛りの数は減ります。 ちなみに、「 時間が長く感じる 」と言うときは、 時 の経過のスピードが遅いように感じることを表します。
私が「 空 が伸びる 」と言うときは、 空(くう)が膨張することを意味します。 一方、「 空間が長くなる 」と言うときは、 物質Aが存在する点 と 物質Bが存在する点 との間隔、 つまり距離、 が長くなるということで、 空 の膨張を表しているのではありません。 移動している慣性系は、 空 が縮んで、 観察者系の空間あたりの被観察系の空間は 1 より大きくなっています。
移動している慣性系( 被観察慣性系;

 系 )では、 静止している慣性系( 観察者の慣性系;
系 )では、 静止している慣性系( 観察者の慣性系; 
 系 )に比べて、 時 は伸び、 空 は縮んでいます。 これを式で表すと次のようになります。
系 )に比べて、 時 は伸び、 空 は縮んでいます。 これを式で表すと次のようになります。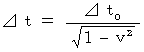 ,
, 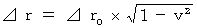
これらの式は、 次のように表すことができます。
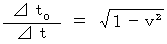 ,
, 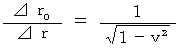
これらの式から、 観察者系の経過時間あたりの被観察系の経過時間は 1 よりも小さくなっており、 観察者系の空間あたりの被観察系の空間は 1 よりも大きくなっていることがわかります。
「 空 が縮む 」とは、 被観察慣性系において光の伝わる距離が短くなることです。 つまり、 観察者の単位時間あたりに観察者の慣性系において光が伝わる距離に比べて、 観察者の単位時間あたりに被観察者の慣性系において光が伝わる距離が短くなることです。
「 静止している慣性系に比べ、 移動している慣性系では、 時 が伸び、 空 が縮んでいる。 」ということは、「 観察者からすると、 移動している慣性系での 時 の経過のスピードが、 観察者の慣性系での 時 の経過のスピードに比べて遅くなっていて、 かつ、 観察者からすると、 移動している慣性系での光の速さが、 観察者の慣性系での光の速さに比べて遅くなっている。 」ということです。 ということは、 移動している慣性系において単位時間あたりに光が伝わる距離と、 静止している慣性系において単位時間あたりに光が伝わる距離とが、 等しくなっていることになります。 これは、 光速不変の原理です。
しかし、 ここで新たな疑問が湧いてきます。 被観察慣性系の運動方向に垂直な方向には、 被観察慣性系の 空 は縮みません。 ということは、 観察者にとっては、 被観察慣性系の運動方向に垂直な方向には、 観察者の 空 での光の伝わる距離と同じ距離だけ、 光が被観察慣性系の 空 を伝わることになります。 したがって、 観察者にとっては、 被観察慣性系の 時 はゆっくりと経過しているのですから、 被観察慣性系の 空 を伝わる垂直方向の光の速さは、 速くなっています。 ということは、 光速不変の原理が崩れていることになります。 そこで、「 相対的垂直速度の法則 」を持ち出してきます。 すると、 被観察慣性系の運動方向に垂直な光の被観察慣性系の 空 を伝わる速さは 1 になり、 光速不変の原理を保つことができます。 これは、 辻褄合わせのこじつけ解釈です。
(2)レーザー光線 と 光源からの光 の違いについて
思い浮かべてください。 今、 あなたは、 まっすぐに引かれた線路の真上 5m に浮いています。 線路をX軸とします。 そして、 あなたは、 a 目 先のY軸上にある電信柱を見ています。 すると、 左側から速さ v x で走ってきた列車に乗っている人が、 あなたの真下に来た瞬間に、 窓から電信柱に向けて矢を放ちました。 矢の速さを v y とします。 すると、 矢は電信柱には当たらず右側へそれてしまうのを、 あなたは観察します。 次に、 左側から速さ v x で走ってきた列車の屋根に取り付けられた光源が、 あなたの真下に来た瞬間に一瞬光を放ちました。 すると、 a 目 後に光が電信柱に当たるのを、 あなたは観察します。
*コメント: ただし、 あなたが電信柱に光が当たったことを認識するのは、
2×a 目 後になります。 なぜなら、 電信柱に当たって跳ね返って
くる光があなたに届くのにさらに a 目 の時間がかかるからです。
アインシュタインの相対性理論は、 こういった認識論を取り扱っ
ている理論ではありません。
ここで、 あなたの観察系での、 矢と光の運動の違いに注目してみましょう。 矢は放たれる瞬間の列車の運動を背負いながら運動していきますが、 光はそれに関係なく運動していきます。 その理由は何でしょうか? それを見つけるために、 まず、 矢の代わりにレーザー光線を電信柱に向けて放った場合について考えてみましょう。 レーザー光線は速さ 1 で飛んでいきます。 なぜなら、 レーザー光線の速さは 1 ですから、 垂直方向の速度の合成式
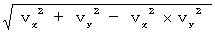 に v y = 1 を代入すると、 1 になるからです。 レーザー光線の飛んでいく方向は、 図1103 のように、 X軸からの角度 θ で表すと、 cos θ = v x になります。 すると、 v x = 0 でない限り、
に v y = 1 を代入すると、 1 になるからです。 レーザー光線の飛んでいく方向は、 図1103 のように、 X軸からの角度 θ で表すと、 cos θ = v x になります。 すると、 v x = 0 でない限り、 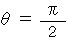 ( Y軸方向 )になりませんので、 レーザー光線は電信柱に当たらないことがわかります。 ということは、 レーザー光線も、矢と同じく、 自分が生まれ出る瞬間の親の運動を背負って運動していくということになります。
( Y軸方向 )になりませんので、 レーザー光線は電信柱に当たらないことがわかります。 ということは、 レーザー光線も、矢と同じく、 自分が生まれ出る瞬間の親の運動を背負って運動していくということになります。図1103
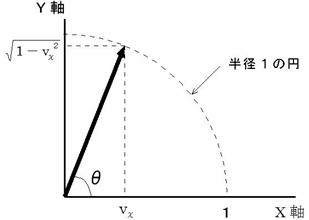
よって、 光源から放たれる光の運動が、 自分が生まれ出る瞬間の親の運動に無関係である理由は、 速さが 1 であるということではないことがわかります。
では、 その理由は何か? それは、 光源から放たれる光は、 波として伝わっていくからです。 つまり、「 光源から放たれる光の真の運動形態は、空間を広がっていく球の表面である。」ということです。 しかし、「 ある空点からある空点まで、結果的に 光子 が等速直線運動をしたように、 見ることができる。」ために、 光源から放たれる光の運動とレーザー光線の運動は混同されやすいのです。
光源から放たれる光であっても、 垂直方向の速さは遅くなるのです。 しかし、 それは、 光の真の運動形態について言ったものではありません。 つまり、 運動している光源から一瞬放たれる光の真の運動形態は、 運動方向が長軸になっている楕円球の表面の膨張ではなく、 静止している光源から放たれる光の運動形態と全く同じで、 空間を拡大していく球の表面です。「 光であっても、垂直方向の速さは遅くなる。 」と言ったのは、 ある空点からある空点まで、 結果的に光が等速直線運動をしたと見られる軌道、 つまり「 結果論的光軌跡 」について言ったものなのです。
(3)運動している物は空間が縮む?
今度はC君が言います。
「 運動している物体は、 運動方向と垂直な方向には縮みませんが、 運動方向に縮みます。 その物体が近づいている場合でも、 遠のいている場合でも。 この事実は、『 ローレンツ収縮 』と言われています。」と。
そこで、 私はC君に言います。
「 まず、 基本的な 第1観察者 と 第0観察者 との関係について考えてみましょう。
同じ長さの棒を持った2人の観察者、 A君 と B君 がいて、 2人はそれぞれの棒を同じ方向に水平に持って、 その方向に相対的に等速直線運動をしながら、 自分の棒の長さと相手の棒の長さを比べているとします。
(式 5-2)より、 次のようになります。
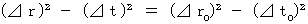 ・・・・(式 11-15)
・・・・(式 11-15)これから、 A君の立場に立って考えます。 A君は次の2つのことを考えています。
a ) 『 B君は、 僕の持っている棒の長さを、 どう見ているのだろう? 』
b ) 『 B君は、 自分の持っている棒の長さを、 どう見ているのだろう? 』
まず、 a )に答えてみましょう。 A君は、 第0観察者の立場になります。 A君が、 自分が持っている静止している棒の両端の空点を同時刻に観測し、 その距離が ⊿x0 であったとします。 この場合、 上記の式に、 ⊿t0 = 0 , ⊿r0 = ⊿x0 を代入して、
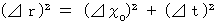 で表すことができます。
で表すことができます。この式は、 B君の座標系での ⊿r と ⊿t の関係を表しています。 ⊿r は、B君が観察する、 A君が持っている移動している棒の長さです。 ⊿t は、 B君が観察する時間で、 A君が持っている棒の両端を測定した絶対時刻の差です。
この式から、 ⊿r ≧ ⊿x0 になっていることはすぐにわかります。 よって、 B君が観察する、 A君が持っている移動している棒の長さは、 A君が観察する、 A君が持っている静止している棒の長さよりも長くなっています。 よって、 B君は、『 止まっている棒が動き出すと、 その長さは長くなる。』と考えます。 したがって答えは、『 B君は、 A君が持っている棒を、 B君が持っている棒よりも長いと見ている。』となります。
これは、 C君の考えと反対です。
次に、 b )に答えてみましょう。 A君は、 第1観察者の立場になります。 A君が、 B君が持っている移動している棒の両端の空点を同時刻に観測し、 その距離が ⊿x であったとします。 この場合、(式 11-15)に、 ⊿t = 0 , ⊿r = ⊿x を代入して、
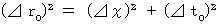 で表すことができます。
で表すことができます。この式は、 B君の座標系での ⊿r0 と ⊿t0 の関係を表しています。 ⊿r0 は、 B君が観察する、 B君が持っている静止している棒の長さです。 ⊿t0 は、 B君が観察する時間で、 B君が持っている棒の両端を測定した絶対時刻の差です。
この式から、 ⊿r0 ≧ ⊿x になっていることがわかります。 よって、 B君が観察する、 B君が持っている静止している棒の長さは、 A君が観察する、 B君が持っている移動している棒の長さよりも長くなっています。 よってB君は、『 動いている棒が止まるとその長さは長くなる。』と考えます。 したがって答えは、『 B君は、 B君が持っている棒を、 A君が持っている棒よりも長いと見ている。』となります。
この場合は、 たしかにC君の言うとおりです。
以上、 a )の答え と b )の答え とが、 まったく逆になっています。 それは、 棒が動いていようが止まっていようが、 棒の長さは座標変換の後で必ず長くなるからです。 それは同時刻性の消失によります。つまり、 座標変換前は ⊿t前 = 0 で、座標変換後は ⊿t後 > 0 だからです。 」
移動している物質の長さをきちんと測定するためには、 同時刻に物質の両端が存在する空点を測定しなければなりません。 私が今C君に反論したように、「 測定の方法が間違ったりする原因などにより、 観察者は現実とは違うように観察して錯覚してしまうだけのことである。」とする考え方を、 私は「 見かけ的相対論解釈 」と言っています。 ただし、 私はこの解釈を正しいと思っているのではありません。
以下の条件が与えられた時、 列車がトンネルの中にスッポリと入ってしまう瞬間があるでしょうか?
列車 の固有長 :

トンネル の固有長 :
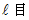
トンネルに対する列車の速さ :

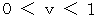
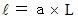 ただし、
ただし、 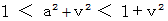
( 答え )
上記の式から、 次の式が導かれます。
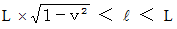
したがって、 列車の固有長は必ずトンネルの固有長よりも長くなっていることがわかります。 よって、 列車がトンネルの中にスッポリと入ってしまう瞬間はないと結論したくなります。 しかし、 ここで、「 ローレンツ収縮 」を思い出してください。 そうですね、 以下の式が成り立っているわけですから、 実際には、 列車がトンネルの中にスッポリと入ってしまう瞬間があることがわかります。
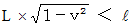
以上が「 列車とトンネルのパラドックス 」です。 パラドックスとは、 一見矛盾しているようでも熟考すると矛盾していない事柄のことを言います。 常識的なニュートン力学では矛盾しているけれども、 真実的な相対性理論では矛盾していないので、 これはパラドックスです。 これで「 めでたし めでたし 」ならばいいのですが、 残念ながらここで、「『 列車とトンネルのパラドックス 』は、 パラドックスでなくて矛盾である。」という意見が出てきます。 その意見の根拠は、 次のようなものです。
「 先ほどの説明は、 トンネルに対して静止している観察者の立場
からの観察である。 列車に対して静止している観察者の立場から
観察すると、 トンネルは列車に対してさらに短くなるので、 列車が
トンネルの中にスッポリと入ってしまう瞬間はないことになります。 」
この根拠に対して納得のいく説明ができてはじめて、「『 列車とトンネルのパラドックス 』がパラドックスであることに、 間違いはありません。」と言うことができますが、 残念ながら、「 列車の乗客にとっても、 列車がトンネルの中にスッポリと入ってしまう瞬間がある。」ということの証明に成功した人は一人もいません。
(4)運動している物は時間がゆっくり進む?
A君は次のように言います。
「 地球に対して速さ v で等速直線運動をしている宇宙船の、 移動方向と垂直に床から天上に向かって放たれた光は、 宇宙船内で観察しているお友達には早く届きますが、 地球上で観察しているあなたには遅く届きます。 ピタゴラスの定理 で得られる分だけ遅く届きます。 つまり、
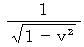 倍、 時間がかかるのです。 したがって、 運動している物質の時間の経過のスピードは遅くなります。 だから、 地球上のあなたからすると宇宙船内のお友達は、 スローモーションで動いているように見えるし、 ゆっくりと歳をとるのです。 浦島太郎が連れていかれた龍宮城とは、 光の速さで運動している極楽浄土のことで、 龍宮城から帰ってきた浦島太郎は歳をとっていなかった。 この物語の作者は、 すでに相対性理論を予感していたのです。
倍、 時間がかかるのです。 したがって、 運動している物質の時間の経過のスピードは遅くなります。 だから、 地球上のあなたからすると宇宙船内のお友達は、 スローモーションで動いているように見えるし、 ゆっくりと歳をとるのです。 浦島太郎が連れていかれた龍宮城とは、 光の速さで運動している極楽浄土のことで、 龍宮城から帰ってきた浦島太郎は歳をとっていなかった。 この物語の作者は、 すでに相対性理論を予感していたのです。(式 5-1)のローレンツ変換の変形式から、 dr0 = 0 の時、
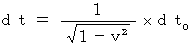 となります。
となります。よって、 第0観察者の時間 dt0 は、 第1観察者の時間 dt に変換されて、 長くなります。 このことから、『 第1観察者からすると、 第0観察者の時間は長く見える。 』と言うことができます。 すると、 たとえば第0観察者が着替えにかかる時間を ⊿t0 とすると、 それを第1観察者が観察すると、 その時間よりも
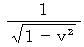 倍 だけ長くなった時間 ⊿t になりますので、 第0観察者がスローモーションで着替えをしているように見えます。 いや見えるだけでなく、 実際にスローモーションになっているのです。」
倍 だけ長くなった時間 ⊿t になりますので、 第0観察者がスローモーションで着替えをしているように見えます。 いや見えるだけでなく、 実際にスローモーションになっているのです。」そこで、 私はA君に次のように言います。
「 しかし、 ここで運動は相対的なものであることを考えてください。 お友達とあなたの関係が、 第0観察者 と 第1観察者 の関係であるとすれば、 同時に、 お友達 と あなた の関係は、 第1観察者 と 第0観察者 の関係でもあるのです。 ということは、 お互いが、 運動している相手のことをスローモーションで着替えているように見るということになります。 ここがパラドックスなのです。
ここで、『 対称的な運動をする双子のパラドックス 』以外の、 定説で解明することのできないパラドックスを、 A君に紹介しましょう。 それは、『 3つ子の時間差Uターンのパラドックス 』です。」
1番目と2番目の兄が、 弟を地球に残して同時に宇宙に向けて旅立ちます。
2人の兄は、 同じ直線上を移動し、 地球に対して光の速さの80%の速さに達したら、 しばらくの間等速直線運動を行い、 地球を離れるときとUターンするときと地球に到着するときには同じ加速度運動をするとします。 1番目の兄がUターンの為の減速運動を開始してから、 弟の時間で2年半後に2番目の兄がUターンの為の減速運動を開始します。
ここで、 2番目の兄が地球に戻ってきたときの3人の歳の差を考えてみましょう。
1番目の兄は弟よりも10歳下になっていたとします。 すると、 2番目の兄は弟より何歳下になっているでしょうか?
1番目の兄の宇宙旅行と2番目の兄の宇宙旅行との違いは、 弟の時間で5年間の等速直線運動です。 その間、 2番目の兄は弟に対して光の速さの80%の速さですから、 次の倍数だけゆっくりと歳を取っていることになります。
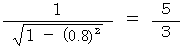
つまり、 弟が5歳の歳を重ねたとき、 2番目の兄は、 3歳の歳を重ねることになります。 したがって、答えは、「2番目の兄は弟より12歳下になっている。」です。
しかし、 ここで、 私たちは矛盾に気づきます。「 弟の時間で5年間の、 2番目の兄の等速直線運動 」というのは、「 移動の相対性 」からすると、「 2番目の兄で5年間の、 弟の等速直線運動 」でもあるので、 この間に、 2番目の兄が5歳の歳を重ねたとき、 弟は、 3歳の歳を重ねることになります。 したがって、 答えは、「 2番目の兄は弟より8歳下になっている。 」ではないか?
<略>

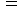
 の条件下での逆ローレンツ変換とは、 本来観察のされ方によって長さが変わる固有時間(
の条件下での逆ローレンツ変換とは、 本来観察のされ方によって長さが変わる固有時間( 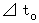 )を無理やりに一定にした場合に、 本来絶対的なものである 絶対時間(
)を無理やりに一定にした場合に、 本来絶対的なものである 絶対時間(  )がどのように変化するのかを見たものなのです。 その上、 第0観察者にとっては、 固有時間(
)がどのように変化するのかを見たものなのです。 その上、 第0観察者にとっては、 固有時間( 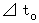 ) = 絶対時間(
) = 絶対時間(  ) ですから、 第0観察者にとっては、 固有時間は絶対的なものになっています。 したがって、 固有時間が絶対的なもので、 絶対時間は相対的なものだと、 反対に思われてしまいやすいのです。
) ですから、 第0観察者にとっては、 固有時間は絶対的なものになっています。 したがって、 固有時間が絶対的なもので、 絶対時間は相対的なものだと、 反対に思われてしまいやすいのです。また、 第1観察者 から 第2観察者 への座標変換とは、 2人の第1観察者がいて、 一方の第1観察者 から 他方の第1観察者 への座標変換を行っているということにほかなりません。 第2観察者も本質的には第1観察者であり、 第2観察者を第1観察者が観察した場合は、 2人の立場が逆になります。 つまり、 第2観察者は第1観察者になり、 第1観察者が第2観察者になるのです。
すると、 新たな疑問が湧いてきます。『 第1観察者の観察時間を第2観察者が観察すると相対的に長くなっているのであれば、 もし、 第2観察者の時間を、 第1観察者が観察すると、 短くなるのではなくて、 さらに長くなってしまうのではないか? 』という疑問です。 しかし、 よく考えてみると、 それでいいのです。 元々、 物質が移動する相対時間の長さは、 物質が移動する空間の長さと同様に、 その物質に対する観察者の速さによって変化するものなのです。 ですから、 ある観察者から別の観察者への座標変換により、 当然、 それは変化するのですが、 逆ローレンツ変換とは、 それを変化しないものと無理やりに条件づけした上で、 絶対時間がどのように変換されるのかを求める道具なのですから、 その結果が現実的な確かなものでなくて当たり前なのです。
等速直線運動している物質( 時計を含む )の 活動 や 生理学的・化学的反応 のスピードを知りたいのならば、 第1観察者が、 それを自分自身の 活動 や 生理学的・化学的反応 のスピードと比べなければなりません。 それなのに、 もう1人の第1観察者がいて、 2人の第1観察者の間で、 逆ローレンツ変換の前と後とを比べ、 その時間の違いを物質の 活動 や 生理学的・化学的反応 のスピードの違いであるとする。 しかし、 それでは結局、『 私からはこう見えるが、 あなたからはそうも見える。 まあそんなものだなあ。』で終わってしまうのです。 」
すると、 A君は私に対して、 次のように念を押します。
「 あなたは、 心臓が1回拍動するのを観察した時間が逆ローレンツ変換によって伸展したときにも、 活動のスピードが変化していない、 と言い切るのですね?」
そこで、 私はきっぱりと答えます。
「 そうです。 心臓が1回拍動するのに要する固有時間が座標変換によっても変化しないとする非現実的な条件の上での結論ですから、 座標変換で心臓が1回拍動する時間が伸びるという間違った結論が導かれるのです。」
観察者の主人公である第1観察者の視点とは、 他人からどう見られるかではなくて、 他人の運動をどう見るかです。 そのための道具は、「 固有時間を相対的なものとし、 絶対時間を絶対的なものとして取り扱う、 定説とは違う、 第1観察者から第0観察者への ローレンツ様変換 」です。 なぜなら、 それは次のように時間を変換するからです。
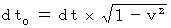
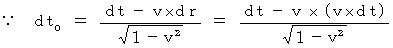
* この式は、(式 11-10)と同じです。 定説のローレンツ変換では、 第1観察
者の絶対時間(
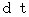 )が 第0観察者の絶対時間(
)が 第0観察者の絶対時間(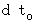 )に変換される、 と
)に変換される、 とします。 そしてそれらは異なるので、 絶対という言葉を消去します。
私見では、 この式の真髄は、 1-3 とします。
1-1. 第1観察者が物質を観察する絶対時間 ⇒
物質の第1観察者によって観察された相対時間
( 1-1. は次のように書くこともできます。)
1-2. 第0観察者が物質を観察する絶対時間 ⇒
物質の第1観察者によって観察された相対時間
( 1-2. は次のように書くこともできます。)
1-3. 物質の第0観察者によって観察された相対時間 ⇒
物質の第1観察者によって観察された相対時間
一方、「 固有時間を相対的なものとし、 絶対時間を絶対的なものとして取り扱う、 定説とは違う、 第0観察者から第1観察者への 逆ローレンツ様変換 」は、 次のように時間を変換します。
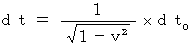
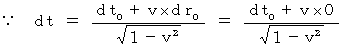
* この式は、(式 11-5)と同じです。 定説では、 ローレンツ変換の逆変換は
第0観察者の絶対時間(
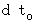 )を 第1観察者の絶対時間(
)を 第1観察者の絶対時間(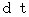 )に変換す
)に変換する、 とします。 そしてそれらは異なるので、 絶対という言葉を消去します。
私見は、 この式を、 一見逆のようですが、 次のように解釈します。
2-1. 物質の第1観察者によって観察された相対時間 ⇒
第1観察者が物質を観察する絶対時間
( 2-1. は次のように書くこともできます。)
2-2. 物質の第1観察者によって観察された相対時間 ⇒
第0観察者が物質を観察する絶対時間
( 2-2. は次のように書くこともできます。)
2-3. 物質の第1観察者によって観察された相対時間 ⇒
物質の第0観察者によって観察された相対時間
私は、 第4章で、「 観察者の主人公である第1観察者の視点に立てば、 逆ローレンツ変換のほうがローレンツ変換よりも大切であることがすぐにわかる。」というようなことを言いました。 なぜなら、 逆ローレンツ変換は、 第0観察者が物質を観察する絶対時間 を 第1観察者がその物質を観察する絶対時間 に変換してくれると考えていたのです。 しかし、 それは、 本来観察のされ方によって長さが変わる固有時間を無理やりに一定であると条件づけした上での、 第1観察者が物質を観察する絶対時間でしかなかったのです。 私は間違っていました。
相対性理論のパラドックスの迷路から抜け出すための1番目の方法は、 第0観察者のミンコフスキー時空間の長さ と 第1観察者のミンコフスキー時空間の長さ を比較することへの執着から自らを解放し、 第1観察者が観察する現実的なイプシュタイン時空間を見つめることです。 つまり、 私たちは、「 固有時間 = 相対時間 」はすべての座標で同じ長さであると無理やり条件づけすることにより、 2つの慣性系の絶対時間の長さの違いを導き出し、 だから「 時間の経過のスピードの違い 」が現実に起こっているのだとする、 ローレンツ変換を、 一度きれいさっぱりと捨て去ることです。
たしかに、 相対性理論は、 座標変換の前後で変化しない光の速さと物理法則から導かれ発見された理論です。 ですから、 相対時間や空間座標など座標変換の前後で変化するものに対して、 どのように変化するのかと深く考察するようになるのも、 無理はないと思います。 しかし、 私たちは、 現実の世界の中で、 比較しなければなりません。 現実の世界では、 万物は、 4次元時空間を速さ 1 で移動し続けています。 大きさが 1 の4次元時空間速度の成分のうち、 目に見える速度が空間速度で、 目に見えない速度が単位絶対時間あたりに経過する相対時間です。 また、 万物は、 物質( 素粒子や電磁波を含む )と物質の衝突による相互関連の 因果律 を保ちながら、 4次元時空間を移動し続けています。 それは、 人間の約束事( ルール )ではなくて、 神様の約束事( 自然の法則 )です。 因果律は座標変換にても保たれます。
* コメント :
私は、 単位絶対時間あたりに経過する相対時間 のことを「 物質の相対時間速度 」といい、「 物質の空間速度 」に対応させています。
そして、 私は、「 物質の相対時間速度は、 物質の活動や生理学的・化学的反応のスピードを決定するものではない。」と考えています。
(5) 座標変換にて不変なのは、 固有時間 か 絶対時間 か ?
考えやすくするために空間を1次元とします。 A君 と B君 と C君 はそれぞれ異なる速度で等速直線運動をしており、 A君 と B君 はそれぞれC君の移動を観察しています。 C君は自分自身が静止しているのを観察しています。 A君 と B君 との関係は、 第2観察者と第1観察者との関係であるとします。
 私見 : 座標変換にて、 絶対時間
私見 : 座標変換にて、 絶対時間 
 が不変である。
が不変である。<< 時計は、 静止していようが移動していようが、 常に絶対時間を刻んでいる。>>
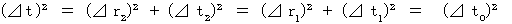
・ ・ ・ ・ ・(式 11-22)
*
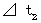 : A君によって観察されたC君の移動相対時間
: A君によって観察されたC君の移動相対時間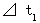 : B君によって観察されたC君の移動相対時間
: B君によって観察されたC君の移動相対時間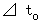 : C君によって観察されたC君の移動相対時間
: C君によって観察されたC君の移動相対時間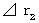 : A君によって観察されたC君の移動空間
: A君によって観察されたC君の移動空間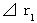 : B君によって観察されたC君の移動空間
: B君によって観察されたC君の移動空間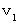 : B君によって観察されたC君が移動する速さ
: B君によって観察されたC君が移動する速さ(式 11-22)より、
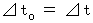
(式 11-22)より、
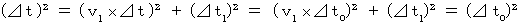
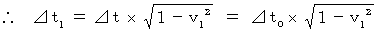
 定説 : 座標変換にて、 固有時間
定説 : 座標変換にて、 固有時間 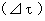 が不変である。
が不変である。<< 時計は、 静止していようが移動していようが、 常に固有時間を刻んでいる。>>
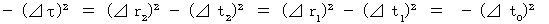
・ ・ ・ ・ ・(式 11-16)
*
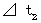 : A君( 第2観察者 )の時間
: A君( 第2観察者 )の時間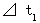 : B君( 第1観察者 )の時間
: B君( 第1観察者 )の時間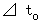 : C君( 第0観察者 )の時間
: C君( 第0観察者 )の時間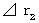 : A君によって観察されたC君の移動空間
: A君によって観察されたC君の移動空間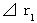 : B君によって観察されたC君の移動空間
: B君によって観察されたC君の移動空間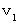 : B君によって観察されたC君が移動する速さ
: B君によって観察されたC君が移動する速さ(式 11-16)より、
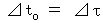
(式 11-16)より、
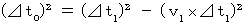
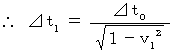
C君は被観察物質であると見なしてほしい。 固有時間は、 常に活動や生理学的・化学的反応をしている物質に備わっている時間である。 固有時間は、 物質の活動や反応が、 ある状態から他の状態へと変化する間の、 時間である。 物質の活動や反応に関して言うならば、 それは物質の移動とは違って、 物質がある状態から他の状態へと変化する事象は、 いかなる観察者にとっても同一の内容である。 つまり、 物質の活動や反応の内容は、 座標変換によって変化をしない絶対的なものである。 たとえば、 A君の座標系では肉が焼き上がっていて、 B君の座標系ではその肉はまだ半生の状態であるというようなことは、 ありえない。 固有時間は物質の活動・反応の状態変化と切り離すことができない。 物質の活動・反応の状態は座標変換によって変化はしないので、 固有時間も座標変換によって変化はしない。 これは当たり前のことである。
一方、 観察者の時間( 座標時間 )は、 物質の運動や活動や反応のパラメーターであり、 時間 と 物質の活動・反応の状態変化 とは切り離して考えることができ、 時間が先で状態変化が後になる。 それは、 グラフで表せば、 座標時間が横軸で状態変化が縦軸の関係である。 物質の活動や反応の内容はすべての観察者にとって同一であるが、 その間の座標時間の長さは観察者により異なる。 そこでグラフを頭に描いてみよう。 観察者によって、 そのグラフは、 横に伸びたり縮んだりしている。 ということは、 観察者によって物質の活動・反応のスピードが異なっているということである。
観察者の時間( 座標時間 )は、 次の式で与えられる。
 ・ ・ ・ ・(式 11-17)
・ ・ ・ ・(式 11-17)(式 11-17)は次のようにも書くことができる。
 ・ ・ ・ ・(式 11-18)
・ ・ ・ ・(式 11-18)(式 11-18)より、次のようになる。
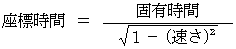 ・ ・ ・ ・ ・(式 11-19)
・ ・ ・ ・ ・(式 11-19)次に、 座標変換によっても固有時間は変化しないので、 固有時間の2乗を定数
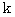 で 表すと、(式 11-17)は次のようになる。
で 表すと、(式 11-17)は次のようになる。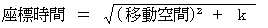 ・ ・ ・ ・(式 11-20)
・ ・ ・ ・(式 11-20)この式を見れば、 移動空間が長ければ長いほど座標時間が長くなっているのが一目瞭然である。 ということは、 観察する物質の移動の速さが速ければ速いほど、 座標時間が長くなっているということである。 固有時間に対して座標時間が長くなるということは、 物質の活動や反応の状態の変化にかかる時間が長くなるということであるから、 観察する物質の移動の速さが速ければ速いほど、 その物質はゆっくりと活動や反応をすることがわかる。 このことは(式 11-19)を見てもすぐに解かる。 物質の移動の速さは観察者によって様々なので、 物質の活動や反応の速さは、 観察のされ方によって違うことがわかる。
さて、 光の伝達( 光子の移動 )の速さはすべての観察者にとって同じ値
 なので、 どの観察者にとっても、 光子の移動については次の式が成り立たなければならない。
なので、 どの観察者にとっても、 光子の移動については次の式が成り立たなければならない。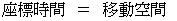 ・ ・ ・ ・ ・(式 11-21)
・ ・ ・ ・ ・(式 11-21)(式 11-17)と(式 11-21)より、 光に関しては、 固有時間が常に
 であることがわかる。 固有時間が
であることがわかる。 固有時間が  であるということは、 光子が活動や反応をしていないということである。
であるということは、 光子が活動や反応をしていないということである。(6)私の空間、 あなたの空間、 あなたたちの空間。
(式 11-17)の「 固有時間 」は「 移動している慣性系の時間 」ですが、「 移動空間 」は「 移動している慣性系の空間 」ではないことに注目してください。「 移動空間 」は「 観察者の空間 」であり、「 観察者の時間 」であるところの「 座標時間 」と同類です。 もし、「 ローレンツ収縮 」する空間を、「 移動している局所的な空間 」ではなく、「 物質が移動している観察者の全空間 」であるとするのなら、 それは、「 元祖ローレンツ収縮への里帰り 」であり、 間違っています。 また、 もし、「 ローレンツ収縮 」する空間を、「 移動している局所的な空間 」ではなく、「 移動している全宇宙空間 」であるとするのなら、 それは、「 非自己絶対静止 & 自己絶対移動 」という非相対論的発想になってしまいます。 私は、 この定説と異なるローレンツ収縮の解釈を「 ローレンツ収縮の全宇宙的解釈( 相対的観察者以外全宇宙移動論 ) 」と言っています。
特殊相対性理論に登場する2人の相対的に等速直線運動をしている観察者 A君 と Bさん は、 それぞれ「 自分は静止していて相手が移動している。」と考えています。 しかし、 ここで1つのトリックをしてみましょう。 「 A君は絶対的に等速直線運動をしていて、 Bさんは絶対的に静止している。」という間違った概念を特殊相対性理論に持ち込んでみます。 その方法は簡単です。 A君は宇宙船に乗っていて、 Bさんは宇宙ステーションにいるという設定をするか、 または、 A君は量子くらいの大きさで、 Bさんは天体くらいの大きさであると設定すればいいのです。 その上に、 Bさんと同じ速度で移動しているCさんを登場させれば、 なおさら結構です。 すると、 みんなそのトリックにひっかかります。 そのとたんに、 A君だけが移動していて、 A君だけがゆっくりと老化していて、 A君の立場のみが「 ローレンツ収縮の全宇宙的解釈( 相対的観察者以外全宇宙移動論 )」になってしまいます。
ミューオンの寿命のパラドックスはこのトリックを利用して説明されていますので、 「 ミューオンの寿命延長が特殊相対性理論の証拠である。」という定説は間違っています。 ミューオンの通常の寿命中にはミューオンは地上には届かないのですが、 地上のミューオンの通常の寿命と同じ余命の観察者の立場からすると、 ミューオンの寿命が延長するために、 自分の死後にミューオンが地上に達することができ、 一方、 ミューオンの立場からすると、 移動している地球とミューオンとの距離はローレンツ収縮しているので、 ミューオンと地上のミューオンの通常の寿命と同じ余命の観察者は生きているうちに出会うことができるのです。
(7)アインシュタインのローレンツ変換導入方法に内在する拡大解釈
ここまで、 私は、「 固有時間とは、 相対時間ベクトルの大きさである。」というイメージで話をしてきましたが、 ここで、 固有時間 と 相対時間 の違いを明確にしておきたいと思います。 たとえば、「 固有時間 」には、「 それぞれの物質に備わっている時間 」というイメージがありますが、 これに対して、「 相対時間 」は、「 観察された時間 」というイメージです。
では、 これから、 絶対時間と比較しながら話を進めていきましょう。
絶対時間は、 観察者( 物質も含める )に備わっている時間であり、 全宇宙的に共通な時間であり、 万物の運動( 移動 や 活動 や 生理学的・化学的反応など )を規定する時間です。 一方、 相対時間は、 物質の4次元時空間の移動の方向の1つであり、「 観察 」という行為によって決まるもので、 物質と観察者との運動関係によって変化する相対的なものです。 物質の移動空間も観察によって決まります。 物質の空間移動に関して言うと、「 絶対的な静止 」はありません。「 静止 」は物質と観察者との運動関係によって決まります。 それと同じことを、 物質の相対時間移動についても言うことができます。
「 相対時間 」の概念は定説には存在しません。 そのかわりに、 定説には「 固有時間 」という概念があります。
固有時間について、 定説は次のように説明します。
「 物質が移動する空間の長さは、 観察のされ方次第で( 座標変換によって )いろいろと変化するが、 物質の移動する固有時間は、 座標変換にてその長さは変わらない。 変わるのは、 固有時間の経過速度である。 また、 1つの慣性系の中に、多数の物質が運動しているとき、 それぞれの物質に備わっている固有時間は、 物質の移動の速さによってその経過速度が異なる。 固有時間の経過速度は、 物質の活動や生理学的・化学的反応のスピードを決定する。 固有時間の経過速度は、 ある行為がなされる間の座標時間に対する固有時間の比率で決まる。 座標時刻は『 共通する、 全ての空間座標点の時刻 』である。 これに対して固有時刻は『 個別な、 空間座標の中を移動している物質点の時刻 』である。 第1観察者にとっては、 固有時刻は『 個別な、 空間座標の中を移動している物質点の時刻 』であるが、 第0観察者にとっては、 固有時間 = 座標時間 であるから、 第0観察者にとっては、 固有時刻は『 共通する、 全ての空間座標点の時刻 』である。」
定説はさらに次のように説明します。
「 今、 あなたは静止している時計A と 等速直線運動をしている時計B とを観察している。 また、 あなたの友達は、 時計Bと同じ速度で移動している。
あなたにとっての時計Bの時を刻むスピードは、 友達にとっての時計Bの時を刻むスピードより遅い。 これは、 固有時間の座標時間に対する比率の違いに由る。
あなたに対して移動していて、 かつ、 友達に対して静止している時計Bの、 針先が0分から1分へと移動する、 その間に経過する以下のものたち ・・・・・
 あなたにとっての時計Bの固有時間
あなたにとっての時計Bの固有時間 あなたにとっての座標時間
あなたにとっての座標時間 友達にとっての時計Bの固有時間
友達にとっての時計Bの固有時間 友達にとっての座標時間
友達にとっての座標時間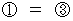 ,
, 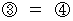 ,
, 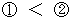 より、
より、 
 ,
, 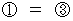 より、
より、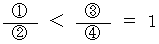
したがって、 あなたにとっての時計Bの時を刻むスピードは、 友達にとっての時計Bの時を刻むスピードより遅いということが言える。
一方、 あなたにとっては、 時計Bの時を刻むスピードは、 時計Aの時を刻むスピードよりも遅い。
時計がどれだけゆっくりと時を刻んでいるのかを調べるためには 、ある座標時間中にその時計の固有時間がどれだけ経過するのかを調べて、 固有時間を座標時間で割った値と 1 とを比べればいいのである。
時計がどれだけの固有時間を経過したのかを調べるためには、 その間にその時計の針先が0分から何分へと移動したのかを調べればいいのである。
座標時間がどれだけ経過したのかを調べるためには、 その間に観察者に対して静止している時計の針先が0分から何分へと移動したのかを調べればいいのである。
あなたに対して移動している時計Bの、 針先が0分から1分へと移動する、 その間に経過する以下のものたち ・・・・・・
 あなたにとっての時計Bの固有時間
あなたにとっての時計Bの固有時間 あなたにとっての座標時間
あなたにとっての座標時間 は、 1分間 です。
は、 1分間 です。 は、 この間に時計Aの針先が0分から何分へと移動したのかを調べることによってわかる。 それは、 1分間よりも大きい。
は、 この間に時計Aの針先が0分から何分へと移動したのかを調べることによってわかる。 それは、 1分間よりも大きい。あなたに対して静止している時計Aの、 針先が0分から1分へと移動する、 その間に経過する以下のものたち ・・・・・・
 あなたにとっての時計Aの固有時間
あなたにとっての時計Aの固有時間 あなたにとっての座標時間
あなたにとっての座標時間 は、 1分間 です。
は、 1分間 です。 は、 この間に時計Aの針先が0分から何分へと移動したのかを調べることによってわかる。 それは、 1分間 である。
は、 この間に時計Aの針先が0分から何分へと移動したのかを調べることによってわかる。 それは、 1分間 である。よって、 次の式が成り立つ。

したがって、 あなたにとっては、 時計Bの時を刻むスピードは、 時計Aの時を刻むスピードよりも遅いということが言える。
以上のように、 観察される物質の固有時間の座標時間に対する比率が相対的なものであり、 観察のされ方によっていろいろと変化するので、 物質の活動や反応のスピードも、 観察のされ方によっていろいろと変化するのである。」
以上が定説ですが、 さて、 これから、 定説の中に固有時間の概念が登場してきた経過についてみてみましょう。
まず、 微小時空間の逆ローレンツ変換から導かれた式に似た式を次に示します。
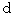 が
が  に置き換わっているだけです。
に置き換わっているだけです。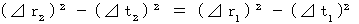 ・ ・ ・ ・ ・(式 11-24)
・ ・ ・ ・ ・(式 11-24)*
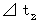 は第2観察者の絶対時間で、
は第2観察者の絶対時間で、 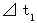 は第1観察者の絶対時間です。
は第1観察者の絶対時間です。この式は、 第1観察者と第2観察者との座標系での同一の物質の運動の共通点を表したものです。 つまり、 この式は、「 ある物質に対して異なる速度で等速直線運動している2人の観察者が、 その物質を観察したとき、 2人にとって、 その物質が持つ『 広義の意味の固有時間
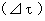 』が等しい。」ということを表しています。
』が等しい。」ということを表しています。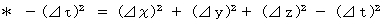
* 狭義の意味の固有時間 : (式 11-24)を、 第1観察者と第0観察者との関係式に
置きなおしたときの、 つまり、
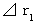
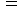
 のときの、
のときの、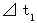 のこと。
のこと。(式 11-24)において、
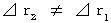 ですから、
ですから、 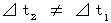 です。 そこで、「 絶対時間 」という既存の概念が覆されました。 2つの慣性系で同一物質の運動を比較したとき、 時間は異なるけれども、 固有時間は等しいので、 固有時間は絶対的なものであり、 時間は相対的なものであるとなったわけです。
です。 そこで、「 絶対時間 」という既存の概念が覆されました。 2つの慣性系で同一物質の運動を比較したとき、 時間は異なるけれども、 固有時間は等しいので、 固有時間は絶対的なものであり、 時間は相対的なものであるとなったわけです。(式 11-24)は、 現在標準になっている方法でローレンツ変換式を導くときの最初に登場します。 第4章で紹介した式を次に示します。
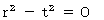 と
と 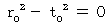 より、
より、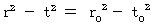 ・ ・ ・ ・ ・(式 11-25)
・ ・ ・ ・ ・(式 11-25)(式 11-25)の左辺は第2観察者の世界で、 右辺は第1観察者の世界です。
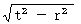 は、 第2観察者が観察する光の固有時間( 私の言葉で言うと、 第2観察者が観察する光が移動する相対時間 )で、 大きさは 0 です。
は、 第2観察者が観察する光の固有時間( 私の言葉で言うと、 第2観察者が観察する光が移動する相対時間 )で、 大きさは 0 です。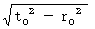 は、 第1観察者が観察する光の固有時間( 私の言葉で言うと、 第1観察者が観察する光が移動する相対時間 )で、 大きさは 0 です。
は、 第1観察者が観察する光の固有時間( 私の言葉で言うと、 第1観察者が観察する光が移動する相対時間 )で、 大きさは 0 です。(式 11-24)と(式 11-25)は同義の式です。
「 この式が光以外のすべての物質の運動にもあてはまるであろう。」として展開いしていくのが、 現在標準になっているローレンツ変換の導入方法です。
では、 これから、 その方法を論理的に検討してみましょう。 まず、 次の2つの事象に注目してください。
事象 A :
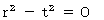 かつ
かつ 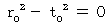 という事象
という事象事象 B :
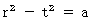 かつ
かつ 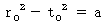 という事象
という事象( つまり、
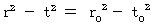 という事象 )
という事象 )事象A を満たす「 4つの数
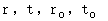 の組み合わせ 」の集まりを 集合A’とし、 事象B を満たす「 4つの数の組み合わせ 」の集まりを 集合B’とします。 また、 ある範囲の中にある たくさんの「 4つの数の組み合わせ 」の中から任意の1つを抽出したときに、 それが常に 事象A を満たすとき、「 事象A はその範囲内において法則である。」と言うことにします。
の組み合わせ 」の集まりを 集合A’とし、 事象B を満たす「 4つの数の組み合わせ 」の集まりを 集合B’とします。 また、 ある範囲の中にある たくさんの「 4つの数の組み合わせ 」の中から任意の1つを抽出したときに、 それが常に 事象A を満たすとき、「 事象A はその範囲内において法則である。」と言うことにします。すると、 この場合、「 もし4つの数の組み合わせが 事象A を満たすならば、 それらの4つの数の組み合わせは必ず 事象B を満たす。」という命題は 真 であり、 かつ、「 もし4つの数の組み合わせが 事象B を満たすならば、 それらの4つの数の組み合わせは必ず 事象A を満たす。」という命題は 偽 です。 このことを、「 4つの数の組み合わせが 事象A を満たすための必要条件は、 それらの4つの数の組み合わせが 事象B を満たすことである。」と表現したり、「 4つの数の組み合わせが 事象B を満たすための十分条件は、 それらの4つの数の組み合わせが 事象A を満たすことである。」と表現したりします。
また、 この場合、「 集合A’は、 集合B’の部分集合である。」または「 集合A’は、 集合B’に含まれる。」という命題は真になります。
また、 この場合、 「 もし 事象A が ある範囲内において法則であるならば、 事象B は その範囲内において法則である。」という命題は 真 であり、 かつ、「 もし 事象B が ある範囲内において法則であるならば、 事象A は その範囲内において法則である。」という命題は 偽 です。 このことを、「『 事象A が ある範囲内において法則である。』という命題が真であるための必要条件は、『 事象Bが その範囲内において法則である。』という命題が真であることである。」と表現したり、「『 事象B が ある範囲内において法則である。』という命題が真であるための十分条件は、『 事象A が その範囲内において法則である。』という命題が真であることである。」と表現したりします。
次に、「 もし 事象A が ある範囲内において法則であるならば、 事象A は その範囲を超えるもっと広い範囲内において法則である。」という命題は 偽 です。 では、「 もし 事象A が ある範囲内において法則であるならば、 事象B は その範囲を超えるもっと広い範囲内において法則である。」というのは、 真 か 偽 か? 答えは当然、 偽 ですね。 実は、 現代の標準的なローレンツ変換導入方法は、 これと同様の論理的展開なのです。 光の伝播の範囲内から、 物質一般の移動の範囲内へと逸脱しています。 ですから、 本来なら「『 事象A が ある範囲内において法則である。』という命題は真であり、 そのための必要条件は、『 事象B が その範囲内において法則である。』という命題が真であることなので、 『 事象B が その範囲を超えるもっと広い範囲内において法則である。』と仮定すると、 ・ ・ ・ ・ 」と表現すべきところを、「 事象A が ある範囲内において法則であるから、 事象B は その範囲において法則である。」という真の命題を持ってきて、 範囲が広がっていることを隠しているために、 集合A’は 集合B’の部分集合ではなくて、 集合B’と合同であるかのような錯覚を与えます。 そのために、 私たちはこの非論理的展開をなかなか見破ることができないのです。
* コメント : もし「 集合A’は、 集合B’の部分集合である。」ならば、
「 集合A’の要素は、 必ず 集合B’の要素である。」と言えますが、
「 集合B’の要素は、 必ず 集合A’の要素である。」とは言えません。
* 誤った論法の例
 最初の設定: a と b は 等しい。
最初の設定: a と b は 等しい。つまり、
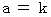 かつ
かつ 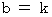 ( ただし、k は 任意の定数 )
( ただし、k は 任意の定数 ) そのための必要十分条件は、
そのための必要十分条件は、 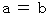 が成り立つことである。
が成り立つことである。 そのための必要条件は、
そのための必要条件は、 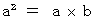 が成り立つことである。
が成り立つことである。*
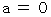 かつ
かつ 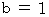 のとき
のとき  が成り立つので、「 十分 」が付かない。
が成り立つので、「 十分 」が付かない。 そのための必要十分条件は、
そのための必要十分条件は、 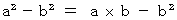
 そのための必要十分条件は、
そのための必要十分条件は、 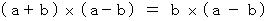
* この式は次のことを表している。( 以上の論法で導かれた結論 : )
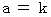 かつ
かつ 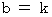 ( ただし、 k は 任意の定数 )
( ただし、 k は 任意の定数 )または
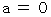 かつ
かつ 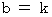 ( ただし、 k は 任意の定数 )
( ただし、 k は 任意の定数 ) 上記
上記  の式の禁じ手は、 以下のごとし。 なぜなら、 両辺を0で割っているから。
の式の禁じ手は、 以下のごとし。 なぜなら、 両辺を0で割っているから。「 そのための必要条件は、
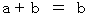 である。」
である。」( 解説 )
・
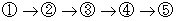 と考察すれば、
と考察すれば、 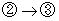 のときに拡大解釈( 仮説の設定 )
のときに拡大解釈( 仮説の設定 )が発生します。
・
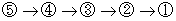 と考察すれば、
と考察すれば、 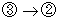 は十分条件の設定になり、 最終的
は十分条件の設定になり、 最終的に導かれる結論が最初の設定を否定してしまうことはありません。
・
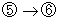 の禁じ手は、「 論理的誤り 」ですので、このようなものが1つ以上含まれた論法
の禁じ手は、「 論理的誤り 」ですので、このようなものが1つ以上含まれた論法によって導かれた結論は、 間違いになります。
・ 「 ローレンツ変換 」が導かれた論法の中には、「 仮定 」はありますが、「 論理的
誤り 」はありません。 しかし、 もし、 この「 仮定 」が間違いであったとしたら、 たと
え「 光速不変の原理 」が否定されなくても、「 ローレンツ変換 」自体が「 論理的誤り 」に
なります。
論理学的手法として、 ある範囲からその内へ内へと向かって、「 ある前提 が この命題 の必要条件となる命題を満たすので、 その前提 は その必要条件となる命題が内包している( 含んでいる )この命題 も満たす。」とか、「 この範囲内 において ある前提 が成り立つのだから、 この範囲が含んでいる ある範囲内 においても その前提 は成り立つ。」と進めていけば、 正しい結論にたどりつくのですが、 反対の方向に進めていくと、「 逆は必ずしも真ならず。 」で、 ある場合には前提が成り立たなくなってしまいます。 こういった失敗は一般的に「 拡大解釈 」と言われています。 とはいっても「 拡大解釈 」自体は悪いことではありません。 これがあるから、 想像が生まれ、 それが新たなものを創造するのです。 大切なのは、「 拡大解釈 」をしていること、 つまり、「 仮定 」をしていることが、 明確になっているかどうかです。
標準的なローレンツ変換の導入方法では、 次のように考えます。( 簡便化のため、 空間を1次元とします。)
相対的に等速直線運動をしている2つの慣性系における、 重なった時の原点から出発した光の運動の方程式は、 次の式たちで表される。

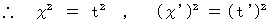
* もし、 2次元空間ならば、 次のように表されます。


そこで、 光を含むすべての物質の運動が、 相対的に等速直線運動をしている2つの慣性系において、 次の式たちで表されると仮定する。
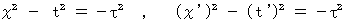
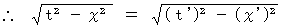
* これを「 座標変換における固有時間不変の原理 」と言おう。
また、
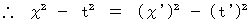 である。
である。現代の標準的なローレンツ変換導入方法( 電磁波的ローレンツ変換導入方法 )においては、 ローレンツ変換は、 ある仮定の上に作られた式だったのです。 その仮定とは、「 相対的に等速直線運動をしている2つの慣性系において、 どんな物質についても、 同一の物質の4次元時空間移動における固有時間( 移動時空間距離 )は等しい。 固有時間は、 その慣性系の中で、 例えば心臓が1回拍動するといったような、 実際の物事の経過時間である。」という仮定です。
* 慣性系とは、 すべての被観察物質が等速直線運動 ( 静止を含む )をし
ていて、 かつ、 観察者が静止している、 観察者の座標系のことです。
元々、 ローレンツ変換は、 マクスウェルの方程式が保存されるような座標変換を求めて、 発見されたものです。 それを私は「 電磁場的ローレンツ変換導入方法 」と言っています。 それは、 電磁気学における相対性原理( 公理1 )から生まれたものです。 その後、 アインシュタインは、 ローレンツ変換が光速不変の原理( 公理2 )からも導くことができることを発見し、 今日の標準的な「 電磁波的ローレンツ変換導入方法 」が確立されました。 したがって、「 電磁波的ローレンツ変換導入方法 」を引き合いに出して、 ローレンツ変換を否定することは間違っています。 元々の「 電磁場的ローレンツ変換導入方法 」に非論理性が潜在していることが証明されない限り、 相対性理論は否定されないのです。
相対性理論の根本であるローレンツ変換は「 固有時間 」が物質の運動を規定する時間であるとし、「 絶対時間 」を否定しています。 ローレンツ変換の実践的な問題点は、 このローレンツ変換から多くの矛盾が導かれることと、 実験が困難なこともあって、 これまでの実験結果が、 ローレンツ変換の現在のような使われ方が正しいのかそうでないのかを、 立証できるレベルに達していないことです。 またローレンツ変換の理論的な問題点は、 それが合同変換ではないということです。 これは、 物理学における座標変換としては、 公認される資格がないのも同然です。 しかし、 その後、 虚数時間の概念が持ち込まれることによって、 ローレンツ変換は座標変換の地位を獲得しました。
物理学における座標変換 は、 座標上の2つの任意の点から構成される相対的位置関係を表すベクトルを、 その大きさを変えないで変換する線形変換です。 このような線形変換は合同変換と言われます。 それは、 直交行列( それ自身と転置行列との積が単位行列になるもの )で表されるテンソルによって担われます。 ローレンツ変換を表現する行列は直交行列でありませんが、 時間を虚数として扱い、 かつ、 次のような「 複素数ローレンツ座標変換 」に変形すれば、 これを表現する行列が直交行列になり、 ローレンツ変換は座標変換を担うテンソルになります。
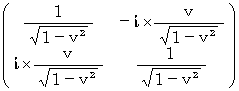
また、 電場を「 虚数時間を光の速さで移動する電荷が作り出す電磁場の虚数成分であり、 それは虚数時間を光の速さで移動する電荷に対して力を作用する。」とすることによって、 マクスウェルの方程式は、「 複素数ローレンツ座標変換 」によって保存されます。 こうして、「 内部矛盾のない特殊相対性理論が確立された。」かのように思えます。
しかし、 私は「虚数時間は物理学に存在してはならない。」と考えていますので、 ローレンツ変換は「 座標変換 」を担う変換ではない と考えます。 私は「 相対論的座標変換は、 時空原点を通過して等速直線運動をする物質が存在しうる時空点の位置ベクトル( 空点 , 相対時点 )を、 その大きさを変えないように変換する変換である。」と考えています。 つまり、「 相対論的座標変換とは、 物質の移動を、 条件を等しくする2人の観察者が観察したときの、 座標変換である。」と考えています。 2人の観察者の条件が等しいとは、「 お互いに相対的移動をしていて、 どちらが移動していてどちらが静止しているのかを区別することができない。」ということと、「2人の観察は同時点同空点に始まり、 2人が観察する物質は、 観察の開始時点に2人と同じ空点に存在する。」ということです。
さて一方、 ルイス・キャロル・イプシュタインは、 次のように仮定したのだと思います。
相対的に等速直線運動をしている2つの慣性系における、 重なった時の原点から出発した光の運動の方程式は、 次の式たちで表されます。

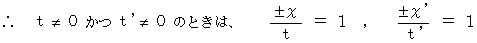
ここで、
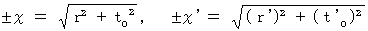 と仮定すると、
と仮定すると、次の式のようになる。
*
 は空間であり、
は空間であり、  は第4の座標軸としての固有時間である。
は第4の座標軸としての固有時間である。* 光の場合は、 常に、
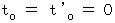 である。
である。 ・・・・(式 11-26)
・・・・(式 11-26)この式は、 光以外の物質の運動についても成り立つと仮定する。
そして、 私は、 イプシュタインの仮定に引き続き、 次のように考えました。
物質は平等に歳を取らなければならない。 したがって、 物質の活動を規定するのは固有時間(
 )ではなく、 絶対時間(
)ではなく、 絶対時間( )であり、
)であり、 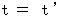 でなければならない。 よって、(式 11-26)は次のようになる。
でなければならない。 よって、(式 11-26)は次のようになる。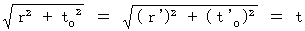 ・・・・(式 11-27)
・・・・(式 11-27)これを「 座標変換における絶対時間不変の原理 」と言おう。
光に限るのならば、 次の式は正しいのです。
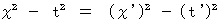
したがって、 光に限るのならば、 ローレンツ変換から導かれる、 次の速度の合成式は正しいのです。
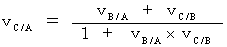 ・・・(式 11-28)
・・・(式 11-28)ここで、 私は、 次のように仮定します。
「 上記の速度の合成式は、 光だけでなく万物にあてはまる。」
第1観察者Bに対して、 速さ
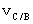 で等速直線運動している物質Cを、 第1観察者Bに対して、 物質Cの運動方向と反対に速さ
で等速直線運動している物質Cを、 第1観察者Bに対して、 物質Cの運動方向と反対に速さ  で等速直線運動している第2観察者Aが観察するとどうなるのか?
で等速直線運動している第2観察者Aが観察するとどうなるのか?(式 11-27)より、
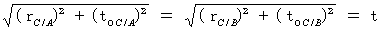
したがって、
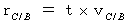
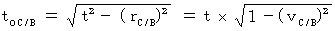
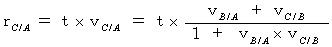

時空間座標を( 空間座標 , 相対時間座標 )で表すと、 座標変換は次のようになります。
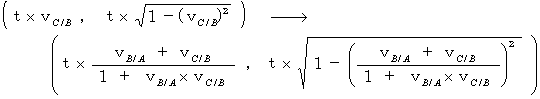
特に、 物質Cが観察者Bであるとき、 自分自身を観察する第0観察者B から 第1観察者A への座標変換は、 次のようになります。
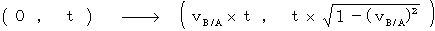
私の慣性系相対性理論の根源になるこの座標変換は、 座標変換によっても光の速さが変化せず、 座標変換によっても物質の速さが光の速さを超えず、 座標変換によっても絶対時間の長さ(

 )が変化しない変換です。 この座標変換については、 次の章でも述べることにします。
)が変化しない変換です。 この座標変換については、 次の章でも述べることにします。