第12章 第3者的観察の放棄 と 新しい座標変換
(1) 第3者的な主観的観察 と 当事者的な客観的観察
まず、「 当事者的な主観的な速度 」と「 第3者的な主観的な速度 」の違いについて説明します。「 当事者的 」とは、 観察の 対象あるいは基準になるもの が静止している場合のことです。 例えば、 静止しているA に対するB の速度は、 当事者的な速度です。「 主観的 」とは、 観察者が携帯している時空間の物差しを用いることです。
思い浮かべてください。 宇宙空間の遠いところに広大な平面鏡があります。 五郎は、 フラッシュを焚き、 それから 2×a 目 後に、 フラッシュが鏡に反射したのを見ました。 五郎がフラッシュを焚いた瞬間、 友子は五郎の背後に存在しており、 高速で鏡の面と平行に等速直線運動をしていました。 友子は、 五郎がフラッシュを焚いてから 2×(a+k)目 後にフラッシュが鏡に反射するのを見ました。 2人とも、 フラッシュが焚かれた時点から、 それが鏡に反射するのを見る時点までの間に、 心臓が1回だけ拍動します。
フラッシュの光は、 速さ 1 で球形に広がっていきます。 五郎が見るフラッシュの光路と友子が見るフラッシュの光路は異なります。
また、 2人の移動の相互関係は相対的 ・ 対称的なものですから、 友子が静止していて、 五郎が移動していると言うこともできます。 このとき、 鏡やフラッシュは友子に対して移動しますが、 そうであっても光の運動は全く対称的ですので、 友子からすると、 友子の心臓が1回拍動する時間は 2×a 目 で、 五郎の心臓が1回拍動する時間は 2×(a+k)目 になります。
そこで、 次の4つの結論を言うことができそうです。
結論1:
「 五郎にとっての、 五郎へ光が伝わる距離 」よりも「 五郎にとっての、 友子へ光が伝わる距離 」のほうが長いので、 五郎にとっては、 友子は五郎よりも遅れてフラッシュの反射を見る。 したがって、 移動している人のほうが、 静止している人に比べ、 ゆっくりと活動する。
結論2:
「 友子にとっての、 友子へ光が伝わる距離 」よりも「 友子にとっての、 五郎へ光が伝わる距離 」のほうが長いので、 友子にとっては、 五郎は友子よりも遅れてフラッシュの反射を見る。 したがって、 移動している人のほうが、 静止している人に比べ、 ゆっくりと活動する。
結論3: |Vg^L(t)t| < |Vg^L(g)g|
「 五郎にとっての、 友子が見る光の、 友子に対する速度 ( Vg^L(t)t )」は、 向きは「 五郎にとっての、 五郎が見る光の、 五郎に対する速度 ( Vg^L(g)g )」と等しく、 大きさは |Vg^L(g)g| = 1 よりも小さい。 したがって、 五郎にとっては、 友子は五郎よりも遅れてフラッシュの反射を見る。 したがって、 移動している人のほうが、 静止している人に比べ、 ゆっくりと活動する。
結論4: |Vt^L(g)g| < |Vt^L(t)t|
「 友子にとっての、 五郎が見る光の、 五郎に対する速度 ( Vt^L(g)g )」は、 向きは「 友子にとっての、 友子が見る光の、 友子に対する速度 ( Vt^L(t)t )」と等しく、 大きさは |Vt^L(t)t| = 1 よりも小さい。 したがって、 友子にとっては、 五郎は友子よりも遅れてフラッシュの反射を見る。 したがって、 移動している人のほうが、 静止している人に比べ、 ゆっくりと活動する。
* 「 五郎にとっての、 友子に対する友子が見る光の相対速度 」は、
「 五郎にとっての、 五郎に対する友子が見る光の速度 」から「 五郎
にとっての、 五郎に対する友子の速度 」を ベクトル的に引き算したも
のです。 つまり、 次の式で表されます。
Vg^L(t)t = Vg^L(t)g − Vg^tg です。
私は、「 a にとっての、 Hの、 b に対する速度 」 = 「 a の第3者的な主観的観察による、 Hの、 移動しているとみなされる b に対する速度 」を Va^Hb で表し、 これを「 第3者的相対速度 」と言っています。 b が a の場合、 つまり Va^Haの場合は、「 当事者にとっての速度 」になります。 光の速度の場合は、 H のかわりに L を用います。 すると、 Va^La の大きさは常に 1 になります。 また、 Va^Lb の大きさは 0 以上 〜 2 以下 で、 一見「 光速不変の原理 」に反しているようですが、「 第3者的相対速度 」は、 ニュートン力学における速度であり、 実在する速度とは違うので、 さしつかえありません。
また、 Va^Hb は、「 a の当事者的な客観的観察による、 Hの、 静止しているとみなされる b に対する速度( Ia^Hb )」とは違います。 Ia^Hb は、「 a の観察による、 b が携帯している 物差し と 時計 」を用いて測定された速度になります。 一方、 Ha^Hb は、 観察者 a に対して静止している 物差し と 時計 を用いて測定されます。
次に、「 第3者的な主観的な速度 」と「 当事者的な客観的な速度 」との違いについて考えてみましょう。
1つの被観察物質と、 第0観察者、 第1観察者、 および第2観察者の、 3人の観察者が存在しているときに、 次のような被観察物質の速度が存在します。
ただし、
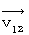 :
:第2観察者の当事者的な主観的観察による、 第1観察者の、 静止しているとみなされる第2観察者に対する、 速度
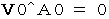
第0観察者の当事者的な主観的観察による、 物質Aの、 静止しているとみなされる第0観察者に対する、 速度
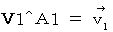
第1観察者の当事者的な主観的観察による、 物質Aの、 静止しているとみなされる第1観察者に対する、 速度
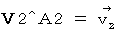
第2観察者の当事者的な主観的観察による、 物質Aの、 静止しているとみなされる第2観察者に対する、 速度
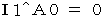
第1観察者の当事者的な客観的観察による、 物質Aの、 静止しているとみなされる第0観察者に対する、 速度

第2観察者の当事者的な客観的観察による、 物質Aの、 静止しているとみなされる第0観察者に対する、 速度
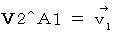
第2観察者の第3者的な主観的観察による、 物質Aの、 移動しているとみなされる第1観察者に対する、 速度
これは、 ガリレイ変換によるニュートン力学における、 速度です。
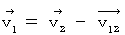 より、 次の式が成り立ちます。
より、 次の式が成り立ちます。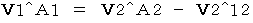
ニュートン力学においては、「 第3者的な主観的観察 」と「 当事者的な主観的観
察 」とは同等なので、
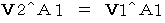 が成り立ちます。 したがって、 上の
が成り立ちます。 したがって、 上の式は次のようになります。
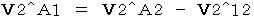
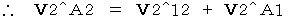 ・ ・ ・ ・(式 1201)
・ ・ ・ ・(式 1201)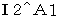 :
:第2観察者の当事者的な客観的観察による、 物質Aの、 静止しているとみなされる第1観察者に対する、 速度
これは、 ローレンツ変換による相対性理論における、 速度です。
1次元空間であれば、 次の式で表されます。
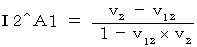
以上7つの速度のうち、 相対性理論が認めていない速度が1つだけあります。 それは、
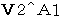 です。 相対性理論では、「 第3者的な観察 」は現実的な観察ではないとされます。 たとえば、「 第3者的な観察 」では、 物質A の 第1観察者に対する速さは、
です。 相対性理論では、「 第3者的な観察 」は現実的な観察ではないとされます。 たとえば、「 第3者的な観察 」では、 物質A の 第1観察者に対する速さは、 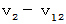 になり、「 当事者的な観察 」による速さ
になり、「 当事者的な観察 」による速さ 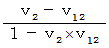 と異なります。 相対性理論の中に「 第3者的観察 」を持ち込むと、 矛盾が生じます。 そして、 これを理由に「 相対性理論は間違っている。 」と間違って考えられてしまいがちです。
と異なります。 相対性理論の中に「 第3者的観察 」を持ち込むと、 矛盾が生じます。 そして、 これを理由に「 相対性理論は間違っている。 」と間違って考えられてしまいがちです。「 第3者的な観察 」が、 観察している物質が移動しているのに対し、「 当事者的な観察 」は、 観察している物質が静止しているという見方をします。 「 主観的観察 」に用いられるのは、 観察者に対して静止している 物差し や 時計であり、「 客観的観察 」に用いられるのは、「 観察者の観察による、 観察の対象になる物質が携帯している 物差し や 時計 」です。
* コメント :
ニュートン力学では、「 第3者的な主観的観察 」=「 客観的観察 」
とされていますが、 これと混合しないようにしてください。
ところで、 私は次のような解釈を「 見かけ的相対論解釈 」と言っています。
「 物質が存在している固有の時点や空点を観察するためには、 その物質が携帯している 物差し と 時計 を用いなければならない。 移動している物質を観察するときに、 自分の慣性系の時空間基準を用いたのでは、 見かけのものしか見えない。 見かけのものから固有のものを導き出してくれるのが、 ローレンツ変換である。」
ちなみに、「 見かけ的相対論解釈 」でもって、 相対性理論の矛盾を解決しようとするのは、 間違いであると、 私は考えています。
絶対的時空間の存在するニュートン力学における座標変換は「 ガリレイ変換 」です。 ニュートン力学においては、「 第3者的な観察 ( 移動している○○に対する□□ )」は「 当事者的な観察 ( 静止している○○に対する□□ )」と同じものです。 一方、 相対性理論で用いられるのは「 ローレンツ変換 」です。 相対性理論は「 第3者的な観察 」を認めていません。 認めているのは「 当事者的な観察 」のみです。「 当事者的な観察 」には、 観察者本人に関する観察である「 当事者的な主観的観察 」と 他人の視点で他人を観察する「 当事者的な客観的観察 」とがあります。
さて、 今度は、 光時計の中の光の運動に関して、「 第3者的な主観的観察 」と「 当事者的な客観的観察 」の違いを見てみましょう。 なお、 ここでは「 第3者的な主観的観察 」は「 ローレンツ収縮 」を考慮に入れていますので、「 第3者的な主観的観察 」は「 ニュートン力学的観察 」から「 相対論的観察」に少し近づいた内容になっています。
内部が真空で内面が鏡で出来た半径
 の球の中心から一瞬光が放たれると、 光は球形に広がっていき、 そして鏡に反射した後、 球形にしぼんでいき、 また球の中心に返ってきます。 この装置を「 正円球形光時計 」と言うことにします。 この正円球形光時計に対して静止している第1観察者が、 1周期の光の運動を観察し、 光の軌跡をすべて黄色で塗りつぶすと、 黄色い正円球ができます。 一方、 この正円球形光時計に対して速さ
の球の中心から一瞬光が放たれると、 光は球形に広がっていき、 そして鏡に反射した後、 球形にしぼんでいき、 また球の中心に返ってきます。 この装置を「 正円球形光時計 」と言うことにします。 この正円球形光時計に対して静止している第1観察者が、 1周期の光の運動を観察し、 光の軌跡をすべて黄色で塗りつぶすと、 黄色い正円球ができます。 一方、 この正円球形光時計に対して速さ  で等速直線運動をしている第2観察者が、 1周期の光の運動を観察し、 光の軌跡をすべて黄色で塗りつぶすと、 運動方向を長軸とする黄色い楕円球ができます。 このとき、 光の発射点と光の収束点は、 楕円球の2つの焦点になっています。
で等速直線運動をしている第2観察者が、 1周期の光の運動を観察し、 光の軌跡をすべて黄色で塗りつぶすと、 運動方向を長軸とする黄色い楕円球ができます。 このとき、 光の発射点と光の収束点は、 楕円球の2つの焦点になっています。コメント : 楕円の円周上の点は、 すべて、 2つの焦点からの距離の和が等しくなってい
ます。 また、 楕円の円周の接線に関しては、 その接点と焦点1を結ぶ線分1
とその接線が作る90度以下の角と、 その接点と焦点2を結ぶ線分2とその接
線が作る90度以下の角とは、 等しくなっています。
第2観察者が見る光の中の光子の2つに注目してください。 1つ目の光子Aは、 正円球形光時計の中心から発射されたあと、 正円球形光時計の進行方向に直進し、 正円球形光時計の鏡上の点Aに衝突します。 2つ目の光子Bは、 正円球形光時計の中心から発射されたあと、 第1観察者に対して正円球形光時計の進行方向と垂直に直進し、 正円球形光時計の鏡上の点Bに衝突します。 ここまでの現象について考えます。
 第2観察者の、 光子が衝突する点についての、 第3者的な主観的観察
第2観察者の、 光子が衝突する点についての、 第3者的な主観的観察
「 第2観察者の第3者的な主観的観察による、 光子Aの、 移動しているとみなされる点Aに対する、 速さ 」は、 次のように表されます。
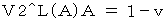
「 第2観察者の第3者的な主観的観察による、 光子Bの、 移動しているとみなされる点Bに対する、 速さ 」は、 次のように表されます。
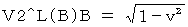

「 第2観察者の第3者的な主観的観察による、 光子Aと衝突したときの点Aの、 光子Aが放たれたときの正円球形光時計の中心に対する、 時間 」は、 次のように表されます。
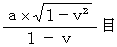
* コメント : 第2観察者にとっては、 正円球形光時計は進行
方向にローレンツ収縮し、 楕円形になっています。
「 第2観察者の第3者的な主観的観察による、 光子Bと衝突したときの点Bの、 光子Bが放たれたときの正円球形光時計の中心に対する、 時間 」は、 次のように表されます。
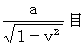

「 第2観察者の第3者的な主観的観察による、 光子Aと衝突したときの点Aの、 光子Aが放たれたときの正円球形光時計の中心に対する、 距離 」は、 次のように表されます。
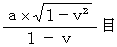
「 第2観察者の第3者的な主観的観察による、 光子Bと衝突したときの点Bの、 光子Bが放たれたときの正円球形光時計の中心に対する、 距離 」は、 次のようになります。
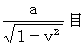
 第2観察者の、 光子が衝突する点についての、 当事者的な客観的観察
第2観察者の、 光子が衝突する点についての、 当事者的な客観的観察
「 第2観察者の当事者的な客観的観察による、 光子Aの、 静止しているとみなされる点Aに対する、 速さ 」は、 次のように表されます。
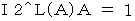
* 次の式から
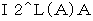 を求めることもできます。
を求めることもできます。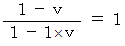
「 第2観察者の当事者的な客観的観察による、 光子Bの、 静止しているとみなされる点Bに対する、 速さ 」は、 次のように表されます。
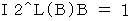

「 第2観察者の当事者的な客観的観察による、 光子Aと衝突したときの点Aの、 光子Aが放たれたときの正円球形光時計の中心に対する、 時間 」は、 次のように表されます。

「 第2観察者の当事者的な客観的観察による、 光子Bと衝突したときの点Bの、 光子Bが放たれたときの正円球形光時計の中心に対する、 時間 」は、 次のように表されます。

* これらの値は、「 第2観察者が観察する、 常に正円球形光時計に
対して静止している時計 」を用いて測定したものです。

「 第2観察者の当事者的な客観的観察による、 光子Aと衝突したときの点Aの、 光子Aが放たれたときの正円球形光時計の中心に対する、 距離 」は、 次のように表されます。

「 第2観察者の当事者的な客観的観察による、 光子Bと衝突したときの点Bの、 光子Bが放たれたときの正円球形光時計の中心に対する、 距離 」は、 次のように表されます。

「 第2観察者の座標系から第1観察者の座標系へのローレンツ変換 」は、「 第2観察者による、 第1観察者についての、 第3者的な主観的観察 」から「 第2観察者による、 第1観察者についての、 当事者的な客観的観察 」への変換であって、「 第2観察者による、 第1観察者についての、 第3者的な主観的観察 」から「 第1観察者による、 第1観察者についての、 当事者的な主観的観察 」への変換ではありません。「 第2観察者による、 第1観察者についての、 当事者的な客観的観察 」と「 第1観察者による、 第1観察者についての、 当事者的な主観的観察 」とは似ていますが異なります。 前者は、 第2観察者が見る第1観察者が携帯している時計や物差しを用いて時空間を計測しますが、 後者は、 第1観察者が見る第1観察者が携帯している時計や物差しを用いて時空間を計測します。 ローレンツ変換をする目的は、「 同一観察者による、 同一物質についての観察を、 ニュートン力学的観察 から 相対論的観察 へと翻訳するため 」です。
「 第1観察者の座標系から第2観察者の座標系への逆ローレンツ変換 」は、「 第2観察者による、 第1観察者についての、 当事者的な客観的観察 」から「 第2観察者による、 第1観察者についての、 第3者的な主観的観察 」への変換であって、「 第1観察者による、 第1観察者に関しての、 当事者的な主観的観察 」から「 第2観察者による、 第1観察者についての、 第3者的な主観的観察 」への変換ではありません。 逆ローレンツ変換をする目的は、「 同一観察者による、 同一物質についての観察を、 相対論的観察 から ニュートン力学的観察 へと翻訳するため 」です。
ローレンツ変換は、 直交座標系から斜交座標系へのベクトル空間の座標変換です。 一方、 逆ローレンツ変換は、 ローレンツ変換の逆変換ですから、 斜交座標系から直交座標系へのベクトル空間の座標変換です。 直交座標系は ニュートン力学的な「 第3者的な主観的観察 」を表し、 斜交座標系は 相対論的な「 当事者的な客観的観察 」を表しています。 たとえば、 9章の 図0901 は「 当事者的な客観的観察 」になり、 図0902 は「 第3者的な主観的観察 」になりますので、 本当は、 図0901 は斜交座標系にしなければならないのです。
(2) マイケルソン ・ モーレーの実験 と ローレンツ収縮
マイケルソン ・ モーレーの実験 とは、 静止している観察者や鏡に対して、 速さ
 でエーテルの風が吹いているときに、 エーテルの風と垂直方向に1往復する光の往復時間 と エーテルの風の方向に1往復する光の往復時間( 往路は逆風、 復路は追風 )とに差があるという理論を確かめようとした実験です。 エーテルの風が吹いていない状況下での光の速さを
でエーテルの風が吹いているときに、 エーテルの風と垂直方向に1往復する光の往復時間 と エーテルの風の方向に1往復する光の往復時間( 往路は逆風、 復路は追風 )とに差があるという理論を確かめようとした実験です。 エーテルの風が吹いていない状況下での光の速さを  とし、 光源と鏡との距離を
とし、 光源と鏡との距離を 
 とすると、 光が1往復する時間の予想値は次のようなものでした。
とすると、 光が1往復する時間の予想値は次のようなものでした。 エーテルの風と垂直方向に1往復する光の往復時間 :
エーテルの風と垂直方向に1往復する光の往復時間 :観察者や鏡に対する光の速さは、 往路も復路も
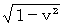 であるから、
であるから、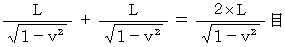
 エーテルの風の方向に1往復する光の往復時間 :
エーテルの風の方向に1往復する光の往復時間 :観察者や鏡に対する光の速さは、 往路が
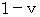 で、復路が
で、復路が 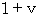 であるから、
であるから、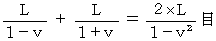
これは、 次のようにして求めることもできます。
往路の光の移動時間を
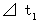 とすると、 次の式が成り立つ。
とすると、 次の式が成り立つ。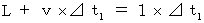
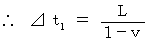
復路の光の移動時間を
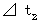 とすると、 次の式が成り立つ。
とすると、 次の式が成り立つ。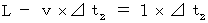
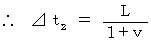
したがって、 求める時間は次のようになる。
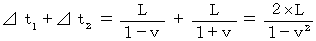
この予想に反して、 マイケルソン ・ モーレーの実験の結果は、
 と
と  は同じ時間でした。 そこで、 ローレンツ と アインシュタイン は次のように考えました。
は同じ時間でした。 そこで、 ローレンツ と アインシュタイン は次のように考えました。 ローレンツによる修正 :
ローレンツによる修正 : エーテルの風と垂直方向に1往復する光の往復時間 :
エーテルの風と垂直方向に1往復する光の往復時間 :元々の
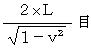 でОK。
でОK。 エーテルの風の方向に1往復する光の往復時間 :
エーテルの風の方向に1往復する光の往復時間 :観察者の空間はエーテルの風の方向に「 ローレンツ収縮 」するので、
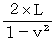 ではなく、 次のようになる :
ではなく、 次のようになる : 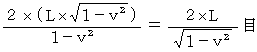
 アインシュタインによる修正 :
アインシュタインによる修正 :マイケルソン ・ モーレーの実験装置に対して静止している観察者を第1観察者とし、 第1観察者に対してエーテルの風と同じ速度で移動している観察者を第2観察者とする。 逆ガリレイ変換前の第1観察者の座標系は「 エーテルの風に吹かれている第1観察者による、 第1観察者についての、 当事者的な主観的観察 」であり、 逆ガリレイ変換後の第2観察者の座標系は「 エーテルの風に吹かれていない第2観察者による、 無風の中を移動している( 相対的なエーテルの風も吹かないと仮定する )第1観察者についての、 第3者的な主観的観察 」である。 前者の方が現実の観察のように思えるので、 そう予想したのであるが、 それはマイケルソン ・ モーレーの実験結果と食い違ってしまった。 ということは、「 第2観察者による、 第1観察者についての、 第3者的な主観的観察 」の方が真実の観察ではないか。 そこで、 第2観察者の座標系で考えてみる。
コメント : 逆ガリレイ変換をすると、 無風になるため光の速さは
 になり、
になり、風方向の光の伝わる距離が

 ではなくなります。
ではなくなります。 エーテルの風と垂直方向に1往復する光の往復時間 :
エーテルの風と垂直方向に1往復する光の往復時間 :往路の光の移動時間 と 復路の光の移動時間 は等しく、 それらを
 とすると、
とすると、次の式が成り立つ。

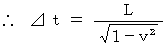
したがって、 求める時間は次のようになる。
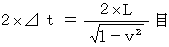
 エーテルの風の方向に1往復する光の往復時間 :
エーテルの風の方向に1往復する光の往復時間 :逆ガリレイ変換によって時間は変わらないので、
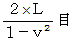 である。
である。これが、 垂直方向の光の往復時間
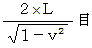 と等しくなるためには、
と等しくなるためには、 が
が 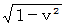 倍 になればいいのだ。
倍 になればいいのだ。つまり、 移動している第1観察者の慣性系の空間は、 移動方向に収縮している。
コメント :
往路の光の移動を「 逆ガリレイ変換 」で表すと、 次のようになります。 ただし、
装置に対して静止している観察者を第1観察者とし、 エーテルの風と同じ速度で移
動している観察者を第2観察者とします。( すると、 第1観察者には速さ
 のエー
のエーテルの風が吹いていて、 第2観察者にはエーテルの風が吹いていないことになりま
す。)また、 第1観察者にとっての、 往路の光が鏡に届くまでの時間は、 上記で求
めたものを使用します。 ( 空間座標値 , 時間座標値 )
第1観察者による、 第1観察者から鏡への時空間位置ベクトル :
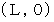
これを第2観察者の座標系に変換すると :
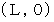
第1観察者による、 往路の光の移動を表す時空間ベクトル :
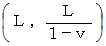
これを第2観察者の座標系に変換すると :
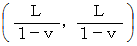
* ガリレイ変換では、 時間不変で、 ガリレイ変換より
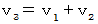
という速度合成式が導かれます。
ガリレイ変換は、 次のように表されます。
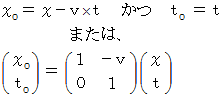
ローレンツの考えは、「 観察者自身の視点から、 エーテルの風が存在し、 かつ、 観察者の空間が収縮する。」でした。 これに対して、 アインシュタインの考えは、「 第3者的観察者の視点から、 エーテルの風は存在せず、 移動している被観察者の空間が収縮する。」でした。「 エーテルの風は存在しない。」とするアインシュタインの方が正しかったのですが、 しかし、 この当時のアインシュタインの考えは、「 ニュートン力学におけるガリレイ変換 」に基づくものでしたので、「 光速普遍&不変 」という「 ガリレイ変換 」を否定する事実の説明において辻褄を合せるために、 アインシュタインにとっても「 ローレンツ収縮 」が必要だったのです。 このころのアインシュタインは「 エーテルの風 」を否定することはできても、 まだ、 エーテルそのものを完全否定するところまでは行っていなかったと言えます。 なぜなら、 エーテルそのものを否定し、 かつ、「 光速普遍&不変 」を肯定するのであれば「ガリレイ変換 」を放棄するしかないのです。 また、 このころは、 アインシュタインも「 観察とは、 『 万物に共通する絶対基準 』 と比較しながら行われる、 絶対的かつ第3者的なものである。」と考えており、「 エーテルの風 」をなくす「 第2観察者 = 無風の神の目 」を必要としたのでした。 これは、 その後に彼が目覚めた「 観察とは、 相対的かつ当事者的なものである。」という発想とは違っていました。
「 ローレンツ収縮 」は、 相対性理論の黎明期には、「 ニュートン力学的観察 」から「 相対論的観察 」への翻訳をするツールでしたが、 その後、 アインシュタインによって、 『 エーテル 』 の存在そのものが否定され、「 ニュートン力学的観察 」から「 相対論的観察 」への翻訳には「 ローレンツ変換 」が用いられるようになりました。 それにより、「 ローレンツ収縮 」は、 当初のローレンツによる「 観察者の空間の収縮 」という概念から、「 被観察移動空間の収縮 」という概念に変化し、 今日の相対性理論の中に生き残っています。
今日の相対性理論は、「 ローレンツ変換 」を相対論的な座標変換の道具であるとし、 特殊相対性理論の土台であるとしていますが、 私は、 「 ローレンツ変換 」とは、 光の移動は別にして、 本来座標変換にて変化する「 固有時間 」を変化しないものであると無理やり設定した上で、 ある観察者によるニュートン力学的な「 第3者的な主観的観察 」を 相対論的な「 当事者的な客観的観察 」に翻訳するツールであり、 2人の観察者の相対論的な観察を対応させる真の相対論的座標変換を担うものではない、 と考えていますので、 その結果生じる「 ローレンツ収縮 」は、 1人の観察者にとっての翻訳による空間の差であり、 2人の観察者の間で現実に空間の差が生じているわけではない、 と考えています。
 A君のニュートン力学的観察
A君のニュートン力学的観察

Bさんのニュートン力学的観察
 A君のニュートン力学的観察
A君のニュートン力学的観察

A君の相対論的観察
 A君の相対論的観察
A君の相対論的観察


Bさんの相対論的観察
さて今度は、 イプシュタインの時空間を用いて、 光時計について考えてみましょう。 光時計の光を反射する向かい合う鏡を、 それぞれ、 鏡A、 鏡B とします。 第1観察者の座標系で、 鏡A は空間原点に静止しており、 鏡B はX軸上に静止しているとします。 そして、 第2観察者がX軸上を負の方向に速さ
 で等速直線運動しています。 第2観察者 と 鏡A がちょうど重なったときに鏡A で反射されたが鏡B に向かい、 そこで反射して再び鏡A に返ってきました。 この状況を、 まず第1観察者の座標系で表します。 図1202 を見てください。 便宜的に空間を1次元で表しています。 図1202 はイプシュタインの時空間です。
で等速直線運動しています。 第2観察者 と 鏡A がちょうど重なったときに鏡A で反射されたが鏡B に向かい、 そこで反射して再び鏡A に返ってきました。 この状況を、 まず第1観察者の座標系で表します。 図1202 を見てください。 便宜的に空間を1次元で表しています。 図1202 はイプシュタインの時空間です。図1202
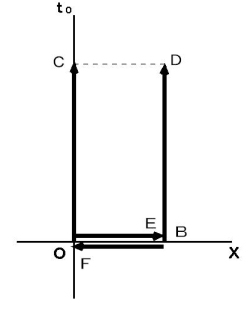
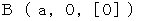
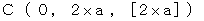

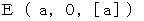
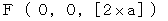
次に、 第2観察者の座標系で表します。 図1202 を逆ローレンツ変換したのが、 図1203 です。 図1203 もイプシュタインの時空間です。
図1203
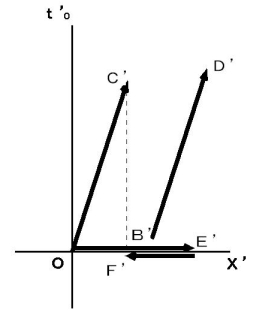
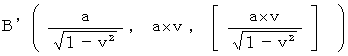

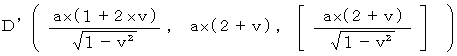
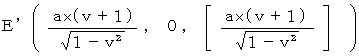
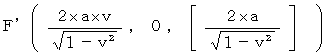
C’ と F’ の絶対時間の値より、 光が1往復するのにかかる時間は、
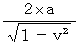 目 であることがわかります。 したがって、 速さ
目 であることがわかります。 したがって、 速さ  で移動している光時計は、 静止している光時計よりも
で移動している光時計は、 静止している光時計よりも 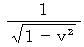 倍 ゆっくりと時を刻みます。 これは 時計のテンポだけが遅れるのではなく、 移動している慣性系の時の経過のテンポが遅れることを意味しています。 つまり、 運動している慣性系の中で静止している物質は、 ゆっくりと活動し、 ゆっくりと生理学的反応を起こしていることになります。 また、 この図から、 光が往路を移動する時間は
倍 ゆっくりと時を刻みます。 これは 時計のテンポだけが遅れるのではなく、 移動している慣性系の時の経過のテンポが遅れることを意味しています。 つまり、 運動している慣性系の中で静止している物質は、 ゆっくりと活動し、 ゆっくりと生理学的反応を起こしていることになります。 また、 この図から、 光が往路を移動する時間は 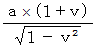 で、 光が復路を移動する時間は
で、 光が復路を移動する時間は 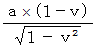 であることもわかります。
であることもわかります。しかし、 移動の相対性より、 移動している慣性系の中で静止している物質からすると、 観察者が静止している慣性系の方が移動していることになるので、 観察者の方がゆっくりと生理学的反応を起こしていることになります。 このように、 ミンコフスキー時空間をイプシュタイン時空間に変更したからといって、「 相対論のお互い様の矛盾 」がなくなるわけではありません。
(3) 移動と活動と観察の哲学
観察様式には次の4種類があります。
 : 自分の時空間基準を用いて、 静止している物質について観察をする
: 自分の時空間基準を用いて、 静止している物質について観察をする「 当事者的な主観的観察 」
ただし、 速度は、 移動している物質ではなく、 基準となる物質に宿るとする。
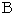 : 自分の時空間基準を用いて、 移動している物質について観察をする
: 自分の時空間基準を用いて、 移動している物質について観察をする「 第3者的な主観的観察 」
 : 自分が観察する移動している物質の時空間基準を用いて、 その物質が静止し
: 自分が観察する移動している物質の時空間基準を用いて、 その物質が静止しているとの視点から、 その物質について観察をする「 当事者的な客観的観察 」
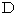 : 自分が観察する移動している物質の時空間基準を用いて、 移動している物質に
: 自分が観察する移動している物質の時空間基準を用いて、 移動している物質について観察をする「 第3者的な客観的観察 」
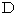 については今まで述べたことがないので、 少し説明しておきます。 例えば次のようなケースです。
については今まで述べたことがないので、 少し説明しておきます。 例えば次のようなケースです。「 ある空点から、 その空点に対して静止しているT君に向かって、 光
と 光の速さのロケット とが同時に放たれたとしましょう。 ロケットには
Sさんが乗っています。
T君からすると、 ロケットと光とに同時に衝突しますが、 Sさんから
すると、 光の速さで近づいてくるT君に対してまず光が衝突し、 その
後にT君がロケットに衝突することになります。 」
上記のSさんのT君についての観察は「 第3者的な主観的観察 」です。 これに対して、 SさんのT君についての「 第3者的な客観的観察 」では、 Sさんが観察するT君の時刻は観察の最初から最後まで
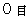 ですので、「 T君が光に衝突するのとロケットに衝突するのは、 同時刻である。」と言えば間違いではないのですが、 しかしこれでは、 光とロケットは放たれた瞬間にT君に衝突することになります。 ということは、
ですので、「 T君が光に衝突するのとロケットに衝突するのは、 同時刻である。」と言えば間違いではないのですが、 しかしこれでは、 光とロケットは放たれた瞬間にT君に衝突することになります。 ということは、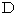 の「 第3者的な客観的観察 」は非現実的なものであると言えます。
の「 第3者的な客観的観察 」は非現実的なものであると言えます。相対性理論の中に、 わざわざニュートン力学的な観察であるところの
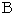 を持ち込んで、 矛盾を生じさせるのは、 相対性理論に対して失礼な自業自得の矛盾です。 しかし、
を持ち込んで、 矛盾を生じさせるのは、 相対性理論に対して失礼な自業自得の矛盾です。 しかし、  と
と  のみを使用しても生じてしまう相対性理論の矛盾は「 お互い様の矛盾 」であり、 本当の相対性理論の矛盾です。
のみを使用しても生じてしまう相対性理論の矛盾は「 お互い様の矛盾 」であり、 本当の相対性理論の矛盾です。相対性理論のパラドックスの迷路から抜け出すための2番目の方法は、 第3者的な観察を捨て、「 当事的な観察 」をすることです。 第3者的な観察に陥ってしまいがちなものには、 次のようなものがあります。
・ 物質と物質との衝突
・ 同時刻の相対性 の説明モデル ( 光子と物質との衝突 )
・ 重力場 や 電場 や 磁場 ( 量子と物質との衝突 )
・ 第3者的相対速度 ( ニュートン力学的速度合成 )
・ ドップラー効果
私が思う、 相対論的な観察とは、 相対的 かつ 主観的 かつ 当事者的 なものです。「 主観的観察 」は、 観察者自身に対して静止している 物差し や 時計 を用いる観察であり、「 当事者的な観察 」は、 観察の対象になる物質が静止しているとみなします。 また、 2人の相対的に移動している観察者が、 同じ物質を観察したときに、 その物質の当事者的主観的な自分に対する移動や出来事 と その物質の当事者的主観的な相手に対する移動や出来事 とを比較するのが、 本当の特殊相対性理論の考え方だと思います。 異なる2つの物質( 例えばお互いの相手の観察者 )の移動や出来事を2人の観察者がお互いに観察して、 それを比較するのが特殊相対性理論ではありません。 つまり、「 AにとってのB 」と「 BにとってのA 」とを比較するのが相対性理論ではありません。 しかし、 第3者的主観的観察と当事者的客観的観察とを対応させているローレンツ変換の副産物としてもたらされる結果は、「 AにとってのBの移動 」と「 BにとってのAの移動 」とが同等であるために生じる、「 Aにとっては A<B 、 かつ、 Bにとっては B<A 。」という「 お互い様の矛盾 」なのです。
さてこれから、 逆ローレンツ変換とは何か? を、「 同時刻の相対性 」を例にとって考えてみましょう。
思い浮かべてください。 列車が猛スピードの等速直線運動で駅を通過しています。 列車の中央にはB君が立っています。 プラットホームにはA君が立っています。 2人がすれちがう瞬間に、 列車の前と後に取り付けられた光源が一瞬ピカッと光ります。
問題1 : B君は、 この2つの閃光をどのように観察するのでしょうか?
( 答え )
第1観察者( B君 )の座標系 :
当事者的な主観的観察 同時刻発 同時刻着
したがって、 B君は、 同時刻に放たれた2つの閃光を同時刻に見る。
問題2 : では、 A君は、 問題1 のことを どのように観察するのでしょうか?
逆ローレンツ変換をしながら考えてください。
 私の見解
私の見解第2観察者( A君 )が見る 第1観察者( B君 )の座標系 :
当事者的な客観的観察 同時刻発 同時刻着

第2観察者( A君 )の座標系での 第1観察者( B君 )にまつわる出来事 :
第3者的な主観的観察 同時刻発 同時刻着
したがって、 A君にとっても、 B君は、 同時刻に放たれた2つの閃光を同時刻に見る。
( 座標変換前の相対論的観察を採用している。)
 今日の相対論者による正解
今日の相対論者による正解第1観察者( B君 )の座標系 :
当事者的な主観的観察 同時刻発 同時刻着

第2観察者( A君 )の座標系での 第1観察者( B君 )にまつわる出来事 :
第3者的な主観的観察 異時刻発 同時刻着
したがって、 A君にとっては、 B君は、 異なる時刻に放たれた2つの閃光を同時刻に見る。
( 座標変換後のニュートン力学的観察を採用している。)
ちなみに、 A君は絶対静止ではなく、 A君とB君の運動関係は相対的です。 したがって、「 A君は、 同時刻に放たれた2つの閃光を同時刻に見るし、 B君にとっては、 A君は、 異なる時刻に放たれた2つの閃光を同時刻に見る。」というのも同時に真実です。
 ローレンツ変換を誤解している人の誤解
ローレンツ変換を誤解している人の誤解第1観察者( B君 )の座標系 :
当事者的な主観的観察 同時刻発 同時刻着

別の第1観察者( A君 )の座標系での 第1観察者( B君 )にまつわる出来事:
第3者的な主観的観察 同時刻発 異時刻着
したがって、 A君にとっては、 B君は、 同時刻に放たれた2つの閃光を異なる時刻に見る。
これは、 結果的に次に述べるニュートン力学による誤解答と同じです。 そうなった理由は、「 ローレンツ変換 や 逆ローレンツ変換 は、 2人の主観的観察の写像である。」と誤解しているからです。
 ニュートン力学者による誤解
ニュートン力学者による誤解第1観察者( B君 )の座標系 :
当事者的な客観的観察 同時刻発 同時刻着

別の第1観察者( A君 )の座標系での 第1観察者( B君 )にまつわる出来事 :
第3者的な主観的観察 同時刻発 異時刻着
したがって、 A君にとっては、 B君は、 同時刻に放たれた2つの閃光を異なる時刻に見る。
 ニュートン力学者から相対論者に成長しきれていない人の誤解
ニュートン力学者から相対論者に成長しきれていない人の誤解( 1916年頃のアインシュタインでさえも勘違いしています。)
第1観察者( B君 )の座標系 :
当事者的な客観的観察 同時刻発 同時刻着

別の第1観察者( A君 )の座標系での 第1観察者( B君 )にまつわる出来事 :
第3者的な主観的観察 同時刻発 異時刻着
ここまでは、 ニュートン力学と同じです。 しかし、 第3者的な主観的観察を否定して当事者の立場に立とうとするあまりに、 さらにここから、 2つの座標系を混同し、 A君にとってのB君の第3者的な観察を、 次のように修正してしまいます。
「 別の第1観察者( A君 )の座標系では、 第1観察者( B君 )は、 2つの閃光をそれぞれ異なる時刻に見る。 ここで、 第1観察者( B君 )の座標系にワープする。 すると、 B君と2つの光源との距離は等しい。 ということは、 2つの閃光は異なる時刻に放たれたことになる。」
したがって、 A君にとっては、 B君は、 異なる時刻に放たれた2つの閃光を異なる時刻に見る。
(4) 新しい「 相対性理論の根本となる座標変換 」の提唱
静止・移動は相対的なものですから、 移動している物質の活動や老化のスピードのみが変化すると矛盾が生じます。 そこで、 私見のような「 当事者的な客観的な観察は、 現実を見ているのではない。」とする考え方が登場してくるわけですが、 これに対して、 今日の相対性理論は、「 その考え方では、 ミューオンの寿命延長を説明することができない。」と一刀両断にします。 しかし、 今日の相対性理論ではこの現象を論理的に証明することができません。( 定説には理論の破たんがあります。)そして、 そこから先、 にっちもさっちもいかなくなって、 ここで足踏みしているのが、 今日の相対性理論だと思います。
私の提唱する「 特殊相対性理論の根本となる座標変換 」は、 ローレンツ変換とは少し異なります。 それは、 次のような点です。
 4次元時空間の4つの座標軸の1つは「 虚数の座標時間 」ではなく「 実数の相対
4次元時空間の4つの座標軸の1つは「 虚数の座標時間 」ではなく「 実数の相対時間 」である。
 座標変換で不変であるのは、「 4次元時空間距離 」であることは同じであるが、
座標変換で不変であるのは、「 4次元時空間距離 」であることは同じであるが、 
の理由にて、「 固有時間 」ではなく「 絶対時間 」である。
 「 座標変換が取り扱えるのは、 時空原点を通過して等速直線運動を行う( 瞬間的に
「 座標変換が取り扱えるのは、 時空原点を通過して等速直線運動を行う( 瞬間的に速度が変化するものは対象となる ) 物質( 量子も含む )の存在する時空点のみであ
る。」という適用の限界があり、 そのことを宣言している。
私の提唱する「 特殊相対性理論の根本となる座標変換 」は絶対時間を不変にする線形変換であり、 座標の回転による変換です。 わかりやすくするために 、空間を1次元であるとし、 4次元時空間を2次元で表すことにします。
一般に、「 時計回りに θ ラジアン 回転させる。」という写像( この場合は等長変換 )は、 次のような線形変換で表されます。
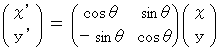 ・ ・ ・ ・ ・(式 1202)
・ ・ ・ ・ ・(式 1202)そこで、 第1観察者系から第2観察者系へは、 次のように座標変換されるとします。
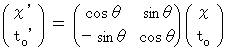
* コメント : 写像 と 座標変換 の違いについて
写像は、 1組の基底が生成するベクトル空間での2つのベクトルの
対応のことです。 座標変換は、 1つのベクトルの2組の基底が生成す
るベクトル空間での表示方法の対応のことです。 たとえば、 ローレン
ツ座標変換は、 1つのベクトルの直交座標系表示と斜交座標系表示
の対応になっています。「 回転 」という等長変換写像は、 逆回転させ
た直交座標系の基底が生成するベクトル空間への座標変換と同じです。
図1208 を見てください。 物質の時空間移動を表したベクトル
 は、 時計回りに
は、 時計回りに  ラジアン 回転し、 ベクトル
ラジアン 回転し、 ベクトル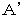 に 座標変換( 正確に言うと、 写像 )されています。
に 座標変換( 正確に言うと、 写像 )されています。図1208

ここで、 座標変換の基本となる、 第0観察者系から、 第0観察者に対して速さ
 で移動している第1観察者系への座標変換を考えてみましょう。 図1209 を見てください。
で移動している第1観察者系への座標変換を考えてみましょう。 図1209 を見てください。図1209
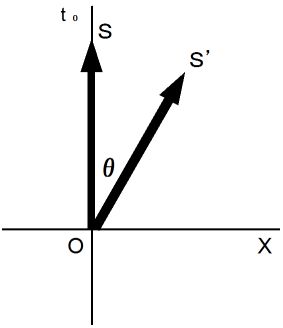
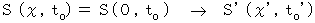 の変換はどのように表されるでしょうか?
の変換はどのように表されるでしょうか?第0観察者にとっての物質の 相対時間 は 絶対時間 に等しいので、

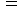
 です。
です。また、
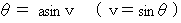 です。
です。したがって次のようになります。
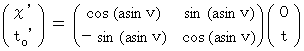
したがって、
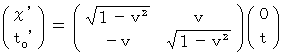 ・ ・ ・ ・ ・(式 1203)
・ ・ ・ ・ ・(式 1203)したがって、
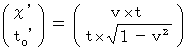
次に、 第0観察者に対して速さ
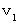 で移動している第1観察者系から、 第1観察者に対して速さ
で移動している第1観察者系から、 第1観察者に対して速さ 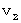 で移動している第2観察者系への座標変換を考えてみましょう。
で移動している第2観察者系への座標変換を考えてみましょう。それには、 第2観察者も基本的には第1観察者であることを利用します。 第2観察者の第0観察者に対する速さ(
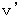 )は、 次のように相対論的速度合成式を用いて求めることができます。
)は、 次のように相対論的速度合成式を用いて求めることができます。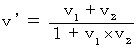
したがって、 第2観察者にとっての物質の時空間移動は、 次の式で表されます。
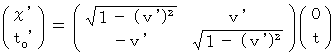
したがって、
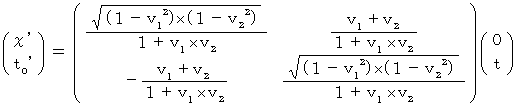
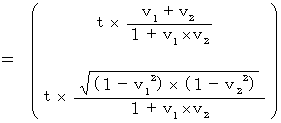
こうして、 第1観察者に対して時空原点を通過して速さ
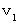 で移動している物質の、 第1観察者に対してその物質の運動と反対方向に速さ
で移動している物質の、 第1観察者に対してその物質の運動と反対方向に速さ 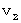 で移動している第2観察者系への座標変換は、 次の式で表されることがわかります。
で移動している第2観察者系への座標変換は、 次の式で表されることがわかります。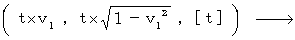
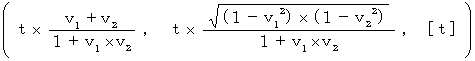
・ ・ ・ ・ ・(式 1204)
この式が、 慣性系相対性理論の根本です。 私はこれを「 ばいおりんの座標変換 」と言っています。
例えば、 時刻
 において、 速さ
において、 速さ 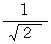 で移動している物質の存在する時空点の、 それを観察している第1観察者に対して、 物質の運動方向と反対向きに速さ
で移動している物質の存在する時空点の、 それを観察している第1観察者に対して、 物質の運動方向と反対向きに速さ  で移動している第2観察者系の時空点への座標変換は、 次のように表されます。
で移動している第2観察者系の時空点への座標変換は、 次のように表されます。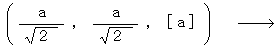
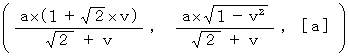
ただし、 ばいおりんの座標変換 を用いても、 第3者的な主観的観察をすることはできません。 というのも、「 第3者的な主観的観察 」は「 ニュートン力学的な観察 」であり、 これは、 相対性理論だけでなく量子論においても間違った観察様式であるとされているからです。 この変換式が通用するのは、 ある時刻に重なり、 かつ、 等速直線運動( 静止を含む )をする、 複数の観察者たち と 1つ以上の被観察物質たち についてのみです。
(5) 定説のローレンツ変換による時空間 と ばいおりんの座標変換による時空間
[ 第0観察者から第1観察者への逆ローレンツ変換による時空間の変換(定説)]
他人(観察者B)は、 私(観察者A)の活動をどう錯覚しているのかしら?
 活動 : 観察者Aの心臓が1回拍動する。
活動 : 観察者Aの心臓が1回拍動する。 その活動が観察者Aによって観察される時間を
その活動が観察者Aによって観察される時間を 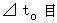 とする。
とする。 その活動が観察者Aによって観察される間の心臓の移動空間
その活動が観察者Aによって観察される間の心臓の移動空間 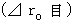 は、 次のようになる。
は、 次のようになる。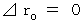
 さて、 その活動が観察者Aに対して速さ
さて、 その活動が観察者Aに対して速さ  で等速直線運動をしている観察者Bによって観察されると、 その時間
で等速直線運動をしている観察者Bによって観察されると、 その時間 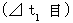 は次のようになる。
は次のようになる。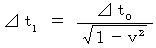
 その活動が観察者Bによって観察される間の心臓の移動空間
その活動が観察者Bによって観察される間の心臓の移動空間 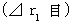 は、 次のようになる。
は、 次のようになる。a)求め方: その1

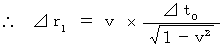
b)求め方: その2
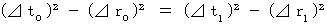
∵ 固有時間は座標変換で不変
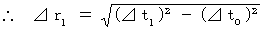
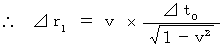
[ 第0観察者から第1観察者へのばいおりんの座標変換による時空間の変換 ]
他人は、 ありのままに私(観察者A)の活動を見てるだけ。
 活動 : 観察者Aの心臓が1回拍動する。
活動 : 観察者Aの心臓が1回拍動する。 その活動が観察者Aによって観察される絶対時間を
その活動が観察者Aによって観察される絶対時間を 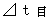 とする。
とする。 その活動が観察者Aによって観察される間の心臓の移動空間
その活動が観察者Aによって観察される間の心臓の移動空間 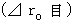 は、 次のようになる。
は、 次のようになる。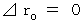
 その活動が観察者Aによって観察される間の心臓の移動相対時間
その活動が観察者Aによって観察される間の心臓の移動相対時間 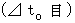 は、 次のようになる。
は、 次のようになる。
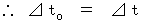
 さて、 その活動が観察者Aに対して速さ
さて、 その活動が観察者Aに対して速さ  で等速直線運動をしている観察者Bによって観察されると、 その絶対時間は
で等速直線運動をしている観察者Bによって観察されると、 その絶対時間は 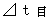 である。 なぜなら、 座標変換にても絶対時間は不変であるから。
である。 なぜなら、 座標変換にても絶対時間は不変であるから。 その活動が観察者Bによって観察される間の心臓の移動空間
その活動が観察者Bによって観察される間の心臓の移動空間 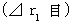 は、 次のようになる。
は、 次のようになる。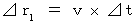
 その活動が観察者Bによって観察される間の心臓の移動相対時間(
その活動が観察者Bによって観察される間の心臓の移動相対時間(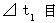 )は、 次のようになる。
)は、 次のようになる。
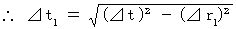
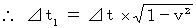
[ 第1観察者から第0観察者へのローレンツ変換による時空間の変換(定説)]
私(観察者B)が錯覚している他人の活動は、 本当のところどうなの?
 活動 : 観察者Bに対して速さ
活動 : 観察者Bに対して速さ  で等速直線運動している観察者Aの心臓が1回拍動する。
で等速直線運動している観察者Aの心臓が1回拍動する。 その活動が観察者Bによって観察される時間を
その活動が観察者Bによって観察される時間を 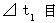 とする。
とする。 その活動が観察者Bによって観察される間の心臓の移動空間
その活動が観察者Bによって観察される間の心臓の移動空間 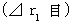 は、 次のようになる。
は、 次のようになる。
 さて、 その活動が心臓に対して静止している観察者Aによって観察されると、 その時間
さて、 その活動が心臓に対して静止している観察者Aによって観察されると、 その時間 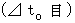 は次のようになる。
は次のようになる。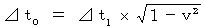
 その活動が観察者Aによって観察される間の心臓の移動空間
その活動が観察者Aによって観察される間の心臓の移動空間 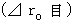 は、 次のようになる。
は、 次のようになる。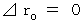
 固有時間は座標変換で不変であることを確かめてみましょう。
固有時間は座標変換で不変であることを確かめてみましょう。
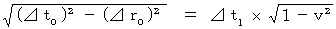
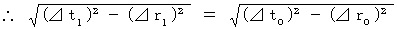
[ 第1観察者から第0観察者へのばいおりんの座標変換による時空間の変換 ]
私(観察者B)は、 ありのままに他人の活動を見てるだけ。
 活動 : 観察者Bに対して速さ
活動 : 観察者Bに対して速さ  で等速直線運動している観察者Aの心臓が1回拍動する。
で等速直線運動している観察者Aの心臓が1回拍動する。 その活動が観察者Bによって観察される絶対時間を
その活動が観察者Bによって観察される絶対時間を 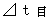 とする。
とする。 その活動が観察者Bによって観察される間の心臓の移動空間
その活動が観察者Bによって観察される間の心臓の移動空間 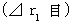 は、 次のようになる。
は、 次のようになる。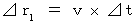
 その活動が観察者Bによって観察される間の心臓の移動相対時間(
その活動が観察者Bによって観察される間の心臓の移動相対時間(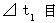 )は、 次のようになる。
)は、 次のようになる。
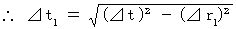
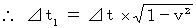
 さて、 その活動が心臓に対して静止している観察者Aによって観察されると、その絶対時間は
さて、 その活動が心臓に対して静止している観察者Aによって観察されると、その絶対時間は 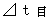 である。 なぜなら、 座標変換にても絶対時間は不変であるから。
である。 なぜなら、 座標変換にても絶対時間は不変であるから。 その活動が観察者Aによって観察される間の心臓の移動空間
その活動が観察者Aによって観察される間の心臓の移動空間 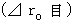 は、 次のようになる。
は、 次のようになる。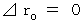
 その活動が観察者Aによって観察される間の心臓の移動相対時間
その活動が観察者Aによって観察される間の心臓の移動相対時間 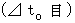 は、 次のようになる。
は、 次のようになる。
相対論の境地
私は、 この私一人。 でも、 私はたくさんいるよ。 私を見る人の数だけ、 私はいるよ。
私はこう見られたい。 でも、 その想いは叶わない。 それは私を見る人が決めること。 けれども、 毎年、 誕生日、 誰も日にちを間違えず、 私を祝いに来てくれる。
私自身を観察する私がいる。 私によって観察される私がいる。 この二人は同じもの。 でも、 あなたによって観察される私は、 この二人とは違う私。
私によって観察される私 と あなたによって観察されるあなた は、 止まったままで時間だけが過ぎていく。 私によって観察される私 と あなたによって観察されるあなた を重ねれば、 なにもかもが見えてくる。 表も裏も見えてくる。
あなたは私にこう言うの。
「 実に面白い。 僕が君からクリスマスカードをもらった事。 僕が君へバースデイカードを送った事。 それらの事が起こる時は、 僕にとってのみ本当の時。 君にとっては、 明確に把握できる時ではあるが、 それは幻の時。 ひょっとしたら、 君が青色だと認識している色は、 僕が赤色だと認識している色かもしれない。」
それでは寂しすぎるから、 あなたの立場で見てみるの。
被観察物質Aは、 1つだけども、 1つじゃない。 それは観察者の数だけ存在する。
多くの観察者たちは、 様々な空間方向に等速直線運動をしている。 彼らは、 彼らの観察の始まりに物質Aと同一の時空点に存在するものとしよう。 物質Aはある点に固定されていて、 その点は時空原点から4次元時空間を光の速さで遠ざかっていく。
被観察物質Aの運動について、 観察者間での座標変換をイメージするとき、 観察者たちは観察中ずっと共通の点に固定されていると考えよう。 彼らの意識は時空原点にとどまり、 彼らの体を乗せた点は相対時間軸上を光の速さで移動する。 様々な観察者からすると、 被観察物質Aが固定されている点は、 時空原点から様々な4次元時空間の方向へ光の速さで広がっていく。
光源から一瞬放たれる光は、 その光一つだ。 そして、 それは、 誰に見られようとも同じ姿をしている。
空間を2次元としたとき、 光源から一瞬放たれる光の運動をイメージしよう。 様々な空間方向に様々な速さで等速直線運動をしている様々な観察者たちの体は、 共通の点上に乗せられ、 時空原点から空間平面と垂直な相対時間軸上を光の速さで移動する。 しかし、 彼等の意識は時空原点にとどまっている。 光の運動は、 すべての観察者にとって、 原点から空間平面を光の速さで広がっていく円で表される。