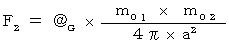第１３章 光源の運動と光の振動数
図1301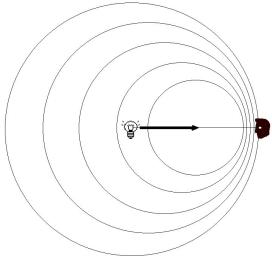
速さ ｖ で運動する光源から放たれるの光の周波数を
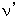とし、 静止している光源から方たれるの光の周波数を 
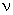とすると、 次のようになります。
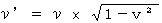・ ・ ・ ・ ・ ・（式 13-1）しかし実際には、 光源が観察者に対する光源の方向と垂直な方向に運動しない限りは、 このとおりになりません。 なぜなら「 ドップラー効果 」が加わるからです。
では実際に、 図1301 のように、 光源が速さ ｖ で観測者に近づいてきている場合を考えてみましょう。 光源は、 １ 目 の時間に ｖ 目 の距離、 観察者に近づいています。 光は、 １ 目 の時間に １ 目 の距離、 進行します。 よって、 ドップラー効果により、 周波数は（式 13-1）の
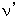よりも 
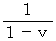倍 多くなっています。 よって、 観察される光の周波数を 
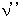とすると、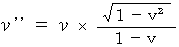
となります。 つまり、
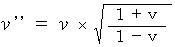になります。 ・ ・ ・ ・ ・（式 13-2）では、光源が観察者に対して、 ｖ の速さで遠ざかっている場合は、 光の周波数はどのようになるでしょうか？ 答えは簡単ですね。（式 13-2）の ｖ を －ｖ に入れ替えて、
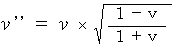となります。＊ コメント ： 音のように、 媒介を伝わる波のときは、 波源 と 媒介 と 観察者 の３つの
運動関係が関与します。 たとえば、 音の速さを
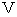とし、 音源 と 観察者 との相対的な速さを
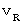とすると、① 観察者が静止したまま、 静止していた音源が観察者に近づきだすと ：
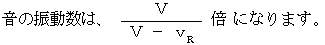
② 音源が静止したまま、 静止していた観察者が音源に近づきだすと ：
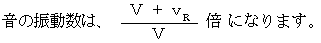
第１４章 ３つの公理と１つの定理
公理
： 物理法則はあらゆる慣性系（ 等速直線運動系 ）において同等である。＝（ 相対性原理 ）
公理
： 光を含めてすべての物質は、 ４次元時空間を速さ １ で移動する。＝（ ４次元時空間速度の公理 ）
公理
： 物質の相互関連の因果律も、 あらゆる慣性系において同等である。万物は、 物質（ 素粒子や電磁波を含む ）と物質の衝突による相互関連の因果
律を保ちながら、 ４次元時空間移動し続けている。
＝（ 因果律の公理 ）
定理
： 質量を持つものは、 重力子が一定の速度で振動していると考える。単位絶対時間あたりの物質中の重力子の振動数を「 静止質量 」といい、
単位相対時間あたりの物質中の重力子の振動数を「 質量 」という。
＝（ 質量と静止質量の定義 ）
今から、 定理
について説明します。 この定理は、 次のように書くことができます。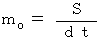
， 
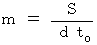
（ Ｓ は重力子が ｄｔ 時間 に 振動する数 ）
すると、
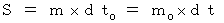・ ・ ・ ・ ・（式 14-1）また、
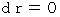の時は、 次の式が成り立つことを思い出してください。
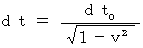・ ・ ・ ・ ・（式 5-3）すると、 上の２つの式より、
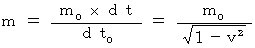・ ・ ・ ・ ・（式 14-2）
第１５章 ４次元時空間運動量
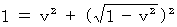の両辺に、 物質の質量の２乗をかけると、
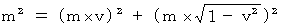になります。
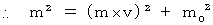
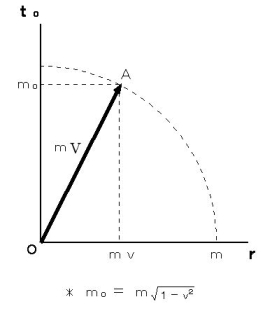
これをイプシュタインの４次元時空間座標で表すと、 その意味が見えてきます。 図1502 を見てください。
図1502
＊ ４次元時空間速度 ：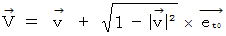 
空間速度 ：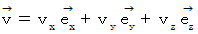 
相対時間速度 ：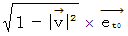 
４次元時空間速度の大きさ ：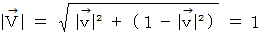 
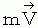は、 物質の４次元時空間速度（ 速度の大きさは １ である ）に質量をかけたものです。 つまり、 ４次元時空間運動量 です。 ４次元時空間運動量の空間成分、 つまり、 いわゆる 運動量 のことを、 私は、「 空間運動量 」と言っています。 また、 ４次元時空間運動量の相対時間成分を、 私は、「 相対時間運動量 」と言っています。 相対時間運動量の大きさは、 物質の 静止質量 になっています。 ４次元時空間運動量の大きさは、 物質の 質量 です。 また、 ４次元時空間運動量の単位は、 質量と同じで、 工 です。
４次元時空間運動量を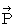 
で表しますと、 以下のようになります。
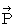
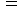
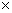
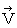・ ・ ・ ・ ・ ・（式 15-4）
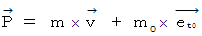
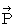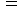
｜｜ ・ ・ ・ ・ ・（式 15-5）
これに関連した式も、 ここで紹介しておきます。
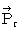
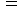
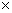
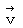・ ・ ・ ・ ・ ・（式 15-6）
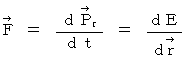・ ・ ・ ・ ・（式 15-7）
＊ ただし、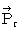 は、 空間運動量です。
第１６章 質量とは何か
これから、 Ｅ ＝ ｍ となることを証明します。 もちろん、 第３章で述べた 目・工・田 単位系 を使用していることが前提になっています。 まず、 考えやすくするために、 ３次元空間は、 Ｘ軸だけの１次元の空間とし、その単位ベクトルを
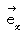で表すことにします。（式 15-6）
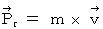より、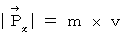 
これに（式 14-2）を代入すると、
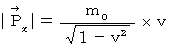・ ・ ・ ・ ・（式 16-1）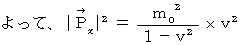
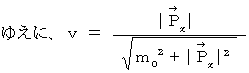・ ・ ・ ・ ・（式 16-2） 次に、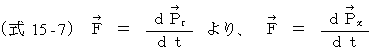
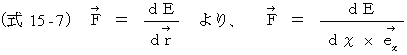
以上の２つの式から、
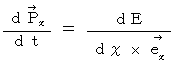
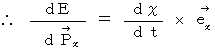
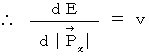
（式 16-3） 最後に、（式 16-2）と（式 16-3）より、
両辺を
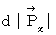で積分すると、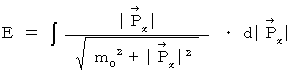
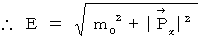
（式 16-4）（式 16-1）を（式 16-4）に代入して、
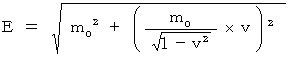
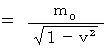
これに、（式 14-2）を代入すると、
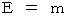
以上より、 質量とは物質の持つエネルギーを表すものであるということがわかります。
＜略＞
第２章で述べた「 ゆきちゃんとまいちゃんのバケツのお水 」のお話を思い出してください。 大切な所をもう一度記述します。
「 観測される物質の単位相対時間あたりのスピン数とは、 観測される
物質の質量であると考えてください。 質量とは、 物質の持つ総エネル
ギーの大きさを表すものです。」
ここで言う「 観測される物質の単位相対時間あたりのスピン数 」とは、 いったいなんでしょうか？ そこで、 第１４章で述べた 定理
を思い出してください。 物質の質量的スピンを担ったり、 空間に光の速さで 重力場 を伝えたりするのが、 重力子です。 物質中の重力子の振動には、 次のような法則があります。「 物質中の重力子の振動は、 どんな観察のされ方をしても、 単位絶対時
間あたりの振動数、 つまり、 重力子の振動の速さ（ 静止質量 ）は一定で
あり、 その振動は相対時間方向にのみ圧縮され、 それが空間を光の速さ
で伝わって行く。 そしてそれは重力場を形成する。」
私はこれを、「 重力子の振動の法則 」と言っています。空間を伝わる重力子の振動は、 物質に作用して重力（ 万有引力 ）を生みます。
第１７章 完全非弾性衝突による静止質量の増大
この章では、 運動量保存法則 と エネルギー保存法則 は成り立つが、 静止質量保存法則 は成り立たないことを勉強しましょう。
思い浮かべてください。 今、 あなたの方に向かって、 左右両方から、 同じ速さ ｖ で２つの紅白の玉が飛んで来ました。 ２つとも同じ静止質量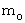
です。 すると、 この紅白の玉の質量 は、 ２つとも次のように表されます。
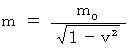・ ・ ・ ・ ・（式 17-1）そして、 紅白の２つの玉は、 あなたの目の前で、 完全非弾性衝突をして、 くっついて止まってしまいました。 このくっついた２個の玉の静止質量を
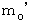とします。では、 これから、
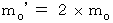ではないということをお目にかけます。
まず、 完全非弾性衝突の前後での運動量保存法則です。衝突前：
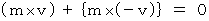
衝突後：
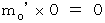
みごと成り立っていることがわかりますね。
次に、 完全非弾性衝突の前後でのエネルギー保存法則です。
衝突前：
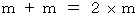
衝突後：
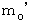
よって、
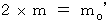です。 ここで（式 17-1）より、 これは次のようになります。
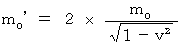・ ・ ・ ・ ・（式 17-2）では、 次に、 白い玉と同じ速度で飛行機に乗って飛んでいるお友達が観察した場合を考えてみましょう。 図1701を見てください。
図1701
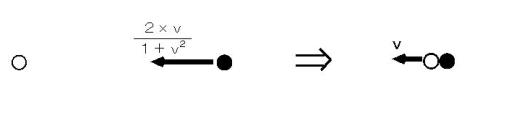
まず、 完全非弾性衝突の前後での運動量保存法則です。
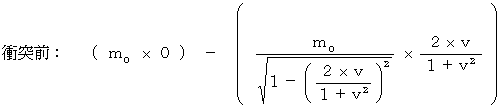
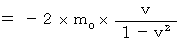
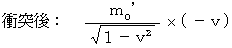
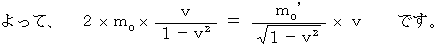
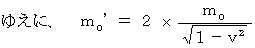・ ・ ・ ・ ・（式 17-3）＜略＞
どうですか、（式 17-2）～（式 17-4）はすべて同じ式になっていますね。 よって「 運動量保存法則 」と「 エネルギー保存法則 」がどちらとも成り立つためには、（式 17-1）と（式 17-2）が真実を表す式であることを認めなければなりません。
そして、 これらの式より、
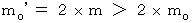であることがわかります。したがって、 静止エネルギーの総和が完全非弾性衝突後に増大していることがわかりました。
第１８章 物質の運動と重力場
第３章で、 ニュートンの万有引力の法則は、 目・工・田 単位系 を用いて次のように表されることを述べました。
・ ・ ・ ・ ・（式 18-1）ただし、
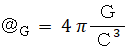
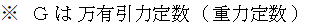
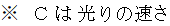
重力場は瞬時に空間を伝わるのではなく 、光と同じ速さで伝わります。 ですから、 上式の「 距離 」とは、 正確に言うと、「 物質２ に働く重力であれば、 物質１ から放たれた重力子が物質２ に到達するまでの距離のこと 」になります。 ここで、 第１６章で述べた「 重力子の振動の法則 」をもう一度、 記載します。
「 物質中の重力子の振動は、 どんな観察のされ方をしても、 単位絶対時間あた
りの振動数、 つまり、 重力子の振動の速さ（ 静止質量 ）は一定であり、 そ
の振動は相対時間方向にのみ圧縮され、 それが空間を光の速さで伝わって行く。」
「 相対時間方向にのみ圧縮された重力子の振動 」は、「 質量 」を表します。
では、 これから、 移動している物質に働く重力 について考えてみましょう。 まず、 思い浮かべてください。 物質Ａ と 物質Ｂ が、 同一直線上をお互いに異なる速度で等速直線運動をしており、 次第に離れていっています。 このとき、 観察のしかたによって次の３とおりが考えられます。
ケース １ ： 物質Ａ とも 物質Ｂ とも異なる速さで等速直線運動している観察者が観察
すると、 物質Ａ も 物質Ｂ も等速直線運動している。
ケース ２ ： 物質Ａ と同じ速度で等速直線運動している観察者が観察すると、 物質Ａは
静止しており、 物質Ｂ は等速直線運動している。
ケース ３ ： 物質Ｂ と同じ速度で等速直線運動している観察者が観察すると、 物質Ａ は
等速直線運動しており、 物質Ｂ は静止している。
ケース １ ～ ケース ３ は、 物質Ａ と 物質Ｂ の運動の関係としては同一の状態で区別することができないものです。 私は、 このことを「 運動学的同等状態 」と言っています。
さて、 ここで、 物質Ａ から 物質Ｂ に働く重力について考えてみましょう。
物質Ａの静止質量 と 物質Ｂの静止質量 を、 それぞれ
，
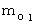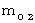とします。物質Ｂ の 物質Ａ に対する速さを
とします。 すると、 物質Ａの物質Ｂに対する速さも になります。（ ただし、 速度は 
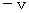になります。）物質Ａ から 物質Ｂ に向けて重力子が放出されたときの２つの物質の距離を ａ 目 とします。
まず、 図1801 を見てください。 これは、 ケース ３ を表しています。
図1801
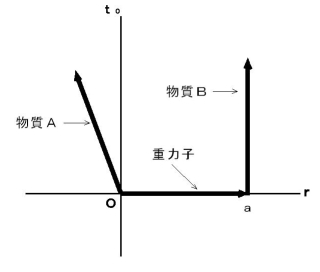
物質Ｂと同じ速度で等速直線運動している観察者が観察する、 物質Ａ から 物質Ｂ に働く重力の大きさ（
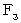）は、（式 18-1）より、 次のようになります。
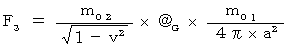・ ・ ・（ 式 18-2 ）次に、 図1802 を見てください。 これは、 ケース ２ を表しています。
図1802
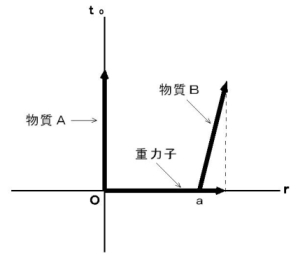
物質Ａと同じ速度で等速直線運動している観察者が観察する、 物質Ａ から 物質Ｂ に働く重力の大きさ（
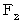）は、 次の式で表すことができそうです。
・ ・ ・（ 式 18-3 ）＊ ただし、 α は ０ より大きい数。
しかし、 これは間違いです。 私たちは、 物質Ｂ がどれだけの重力を受けるのかを求めようとしています。 そこで私たちは、 物質Ｂ という当事者の立場に立ってこれを考えなければなりません。 なぜならば、 第３者的な見解に陥ると、 重力子の速さが光速よりも速くなったり遅くなったりするからです。 実際に見てみると、 ケース ３ では、 第１観察者にとっての、 重力子の物質Ｂに対する速さは、 当事者の物質Ｂにとっての実際の速さ １ になっていますが、 ケース ２ では、 第１観察者にとっての、 重力子の物質Ｂに対する速さは、 見かけの速さ １－ｖ になっています。 もちろん、 当事者にとっての実際の重力子の速さは、
です。したがって、 ケース ２ で重力の大きささを求める場合は、 まず ケース ３ で重力の大きさ（
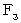）を求めて、 それから、「 ケース ２ と ケース ３ は、 物質Ａ と 物質Ｂ について 運動学的同等状態 であるから、 重力の大きさ 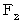は、 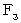に等しい。」として、 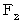を求めなければならないのです。今度は、 物質Ａ と 物質Ｂ とを結ぶ線分に垂直な方向に移動する観察者からは、 重力 がどうなるのかを考えてみましょう。
図1803 を見てください。 これは第１観察者の座標系です。 物質Ａ が時空原点に存在した瞬間に重力子を放ち、 それが 物質Ｂ に ａ 目 の時間後に到着するまでを、 イプシュタインの４次元時空間座標で表したものです。（ 便宜的に空間を２次元で表しています。）物質Ａ と 物質Ｂ の距離は ａ 目 であり、 どちらとも静止しています。
図1803
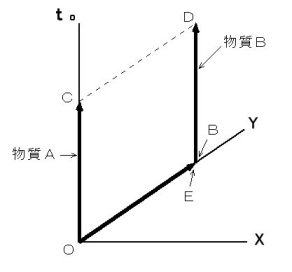
Ｂ（ ０， ａ， ０， ［０］ ） Ｃ（ ０， ０， ａ， ［ａ］ ）
Ｄ（ ０， ａ， ａ， ［ａ］ ） Ｅ（ ０， ａ， ０， ［ａ］ ）
第１観察者にとっての、 物質Ａ が 物質Ｂ に及ぼす重力の大きさ（
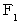）は、 次のようになります。
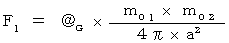・ ・ ・ ・ ・（ 式 18-4 ）では、 これを、 Ｘ軸の負の方向に速さ ｖ で移動している第２観察者が見たらどうなるでしょうか？ 第２観察者への座標変換は、（式 8-5）と（式 8-6）を用います。 図1804 を見てください。
図1804
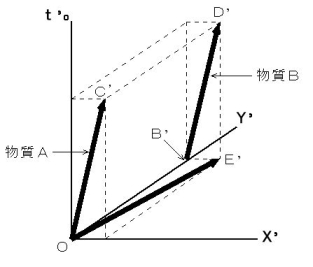
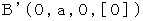
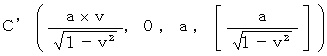
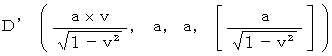
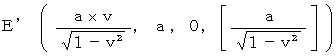
第２観察者にとっての、 物質Ａ が 物質Ｂ に及ぼす重力の大きさ（
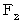）は、 いくらになるでしょうか？ この問題も先程と同様に、 重力を受ける物質が移動しているために、 第２観察者にとっての、 重力子の物質Ｂに対する速さは、「 第３者的な相対的な速さ 」であり、 １ ではありません。 つまり、 重力子の第３者的相対速度は、 方向がＹ軸方向で、 大きさが 
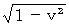になっています。 さらに、 図1804 は、 逆ローレンツ変換によって求められた、 膨張する４次元時空間を逸脱した仮想空間です。 そこで、 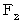を求めるためには、 先程と同様にして、 物質Ａ と 物質Ｂ について 運動学的同等状態 で、 かつ、 重力を受ける物質Ｂ が静止している慣性系で、 重力の大きさを求めなければなりません。 図1803 の第１観察者の観察する物質たちの運動関係は、 図1804 の第２観察者の観察する物質たちの運動関係に対して、 運動学的同等状態 です。 したがって、 
ですから、（ 式 18-4 ）より、 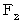は次のようになります。