第１９章 電流と電気量
（１）電流とは何か？
「 電流の定義をしてみてください。」という質問をしたら、 ２人から次のような答えが返ってきました。
Ａ君： 「 電流とは、 単位時間あたりに、 ある範囲の平面を通過する、 総電荷です。
よって、 電流の単位： アンペア（ Ａ ） と 電気量（電荷）の単位： クーロン（ ｃ ）
の関係は、 Ａ ＝ ｃ ÷ 秒 で与えられます。」
Ｂ君： 「 電流は、 次の式で表現されます。
× 微少空間距離 ＝ 電荷 × 
・ ・ ・ ・ ・（式 19-1） 」私は、 Ａ君の答えもＢ君の答えも、 正しいと思います。
（式 19-1）の左辺は「 電流素片 」と言われます。
私は、（式 19-1）の右辺を「 空間電気量 」と言っています。
（２）４次元時空間運動量 と ４次元時空間電気量 の対応
一般的には、 電荷 ＝ 電気量 ですが、 私は、 電気量 を 電荷 と違ったものとして定義しています。 電気量 を 運動量 に相当するものとして定義しています。 私は、 電荷 のことを「 電荷量 」と言っています。
「 運動する質量 」と「 運動する電荷量 」は、以下のように対応しています。
質量（ ｍ ） ←－－→ 電荷量（ ｑ ）
４次元時空間運動量
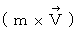←－－→ ４次元時空間電気量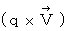 
空間運動量
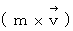←－－→ 空間電気量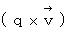 
相対時間運動量 ←－－→ 相対時間電気量
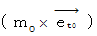
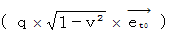
＊ ４次元時空間速度 ：
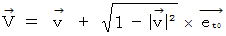
空間速度 ：
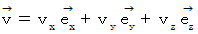
相対時間速度 ：
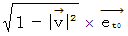
４次元時空間速度の大きさ ：
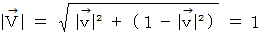
質量とエネルギーは、 観察のされ方によって変わってくる量です。 そういう意味では、それらは一見スカラーのようですが、スカラーとは違います。 （ スカラーとは座標変
換にても変化しない量です。 たとえば電荷量です。 一方、 ベクトルは方向を持つ量で、
座標変換によって量や方向が変化します。）
そこで、 私は、 スカラーに似ているこれらの量を「 バイブ 」と言っています。
運動量 と 電気量は、 ベクトルです。
相対時間運動量の大きさ ＝ 静止質量相対時間電気量の大きさ ≠ 電荷量
重力子の振動の速さ ＝ 静止質量光子の電気的振動の速さ ＝ 電荷量
⑤ 座標変換で保存されるもの ＝ 静止質量
座標変換で保存されるもの ＝ 電荷量
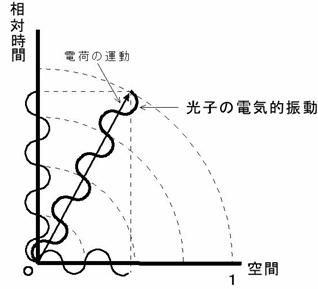
重力子の振動の伝わり方 と 光子の電気的振動の伝わり方 には違いがあります。それは、 図1601 と 図1902 の違いです。図を再掲しておきます。
図1601
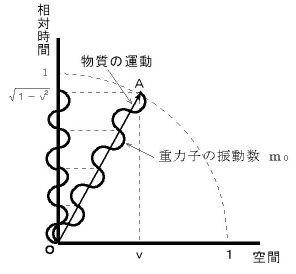
図1902
第２０章 ２つの電荷の間に働く電気力
（１）書き直されたクーロンの法則第３章で、 クーロンの法則は、 目・工・田 単位系 を用いて次のように表されることを述べました。
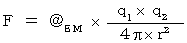・ ・ ・ ・ ・（式 20-1）しかし、 私の慣性系相対性理論では、 クーロンの法則は次のように書き直されます。
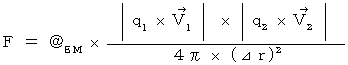
・・・・・（式 20-2）
私は、（式 20-2）を「 電荷間電気力 」と言っています。
では、 この式について説明していきましょう。
まず、 第１９章で述べた「 光子の電磁場的振動の法則 」を思い出してください。 もう一度、 記載しておきます。
「 電荷量を持つ物質中の光子の電磁場的振動は、 どんな観察のされ方をしても、
単位絶対時間あたりの振動数、 つまり、 光子の電磁場的振動の速さ（ 電荷量 ）
は一定であり、 その振動は、 そのまま伝わっていくものと、 空間成分 と 相対時
間成分 に分解されて その振動の空間成分のみが伝わっていくものとの２つに分
かれる。 それぞれが空間を速さ
で伝わっていく。前者は、 電場を形成してクーロン力を生み、 後者は、 磁場を形成してローレン
ツ力を生む。」
そのまま空間を伝わる光子の電磁場的振動とは、 ４次元時空間電気量
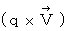のことです。 これがクーロン力を生み出すと考えられます。 しかし、 目・工・田 単位系 では 
なので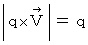 
です。 したがって、 従来のクーロン力の式でいいと思うかもしれませんが、 それではいけません。 その理由は、 クーロン力の定義式の定数には、 ローレンツ力の定義式に含まれていないていない「 光の速さ（ Ｃ ）の２乗 」が含まれているからです。（ 目・工・田 単位系 では光の速さは です。）（式 20-2）は、 クーロン力の定義式ですので、 きちんとしなければなりません。 そうです、 クーロン力を生むのは、 電荷量ではなくて、 ４次元時空間電荷量だったのです。 クーロン力の真の定義式を ＳＩ 単位系 で表すと、 次のようになります。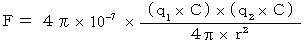
最後に、 ４ π は、 球の表面積に由来するものであることを言って、（式 20-2）の説明を終わります。
（２）電場について
電場を作る３つのものについて述べましょう。
４次元時空間電気量 大きさが変化する磁場 運動する磁場は、 クーロンの法則の私バージョンです。（ 電荷間電気力 ）は、 ファラデーの電磁誘導の法則 と言われています。を私は､「 仮想電場の法則 」と言っています。 その内容は次のようなものです。「 速度
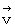で運動する磁場 
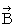が形成する仮想電場 
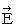は、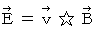
（ 
は外積演算子 ） である。」この法則は、 磁場の中で運動する電荷量に働く力（ ローレンツ力 ） から導くことができます。
では、 やってみましょう。 磁場の中で等速直線運動する電荷量を、 電荷量と同じ速度で運動しているＡ君が見たらどうなるか考えてみてください。 空間電気量
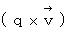は 
になります。 ローレンツ力は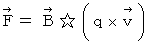 
ですから、 Ａ君にとっては電荷量に作用するローレンツ力は になってしまいます。 これでは相対性原理に反してしまいます。 そこで、 Ａ君にとっては、 そこに電場が形成されていると考えるのです。 具体的には、 次のようになります。磁場
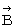が存在する空点において、 それと垂直な方向を向く空間電気量 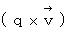が受けるローレンツ力（ 
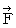）は、 次の 図2001 で表されます。図2001
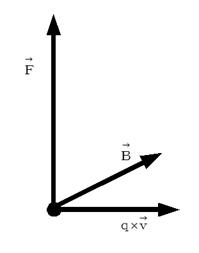
これをＡ君の立場から見ると、 電荷は静止していて、 磁場が運動していることになるので、「 仮想電場の法則 」より、 図2002 のような仮想電場（
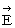）ができていることになります。 磁場の移動速度の向きは 図2001 と反対になっています。図2002
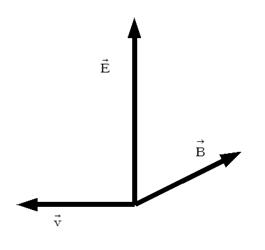
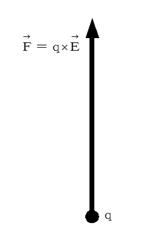
すると 図2003 のようなクーロン力が電荷に作用していることになり、 元々のローレンツ力と等しくなります。
図2003
第２１章 ２つの電荷の間に働く磁気力
（１）磁場について磁場を作る２つのものについて述べましょう。
「 相対的空間電気量 」相対的空間電気量とは、 電気的に ０ の空点が電気的に引き裂かれる時の、
－ の電荷量に対する ＋ の電荷量の相対的な空間速度に、 引き裂かれる正の
電荷量をかけて求められる、 ベクトルのことある。
大きさが変化する電場 は、 大まかに言えば、 導線の中を流れている電流と言ってもかまいません。 導線の中を流れている電流の場合は、 ビオ ・ サバールの法則 と言われています。 はマクスウェルによって発見されたものです。ここで、
に関して大切なことを言っておきます。 それは、 単に空間電気量が磁場を作るのではないということです。 もし、 単なる空間電気量が磁場を形成するのであれば、 クーロン力 と ローレンツ力 とをベクトル的に加えて得られる電荷量間の力が、 第０観察者と第１観察者とで異なるという矛盾が生じてしまいます。先ほど、「 電場は、ある空点に重なって電気的に ０ になっている ＋ と － の電荷量を正反対に引き裂く力を生じさせる場でもある。」 と言いましたが、 今度は、「 ある空点に重なって電気的に ０ になっている ＋ と － の電荷量が正反対に引き裂かれた時には磁場が生じる。」 と言うことができます。 導線の中を流れている電流を思い浮かべてください。 導線の中では、 ＋ の電荷量は静止しており、 － の電荷量をもつ電子たちが運動をしているのですが、 それは、 マクロ的には、 導線内のすべての空点で、 電気的に ０ になっている ＋ と － の電荷量が絶え間なく正反対に引き裂かれていると考えることができます。
（２）相対的空間電気量が空間電気量に作用する力
電気的に ０ の空点が ＋ と － に引き裂かれる時の「 相対的空間電気量 」を
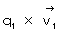とし、 電荷量 ｑ２ を持つ物質の空間速度を 
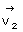とします。では、 等速直線運動をしている電荷量 ｑ２ が、 相対的空間電気量
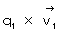から受ける力について、 考えてみることにしましょう。第３章で、 ローレンツ力は、 目・工・田 単位系 を用いて次のように表されることを述べました。
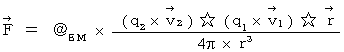・ ・ ・ ・（式 21-1）コメント：
は外積演算子を表す。 例えば、 次のようになる。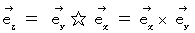
しかし 、私の相対性理論では、 ローレンツ力は次のように書き直されます。 私は、 これを「 電荷間磁気力 」と言っています。
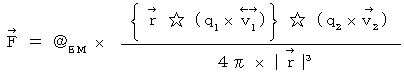
・ ・ ・ ・ ・ ・（式 21-2）
＊ ただし、
ｑ１ は、 電気的に ０ の空点が電気的に引き裂かれる時の、 引き裂かれる電荷量
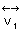は、 電気的に ０ の空点が電気的に引き裂かれる時の、 － の電荷量に対する＋ の電荷量の相対的な空間速度
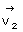は、 電荷量 ｑ２ の空間速度 （ 
は、 空間電気量 ）｜
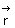｜ は、 相対的空間電気量 
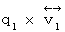から放たれた光子が電荷量 ｑ２ に到達するまでの距離
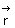の方向は、 光子が放たれたときの、 電荷量 ｑ２ の 電荷量 ｑ１ からの方向ローレンツ力は、 １つの現象をとって言うと、「 同じ方向に流れる電流の間に働く引力 」です。
では、（式 21-2）を、 仮想電場を用いて証明してみましょう。 まず、 その概略から説明します。
はじめに、「 電荷間磁気力 」を受ける空間電気量を形成している電荷量を持つ物質を静止させます。 つまり、 その物質と同じ速度で等速直線運動をしている観察者がどう観察するのかを考えるのです。 そして次に、「 電荷量はローレンツ力（ 磁力 ）を受けないで、 仮想電場による力を受ける。」ので、「 電荷量の受ける力の大きさは○○である。」と言います。 そして最後に、「 静止または等速直線運動をしている観察者であれば、 誰が観察しても電荷量が受ける力は同じである。」という相対性原理より、「 電荷間磁気力は、仮想電場による力と同じ大きさである。」と言い切ります。
では、 実際にやってみましょう。
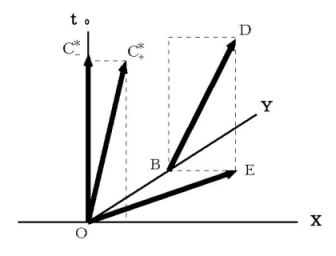
まず、 図2101 を見てください。 時空原点に存在する －ｑ１ の電荷量は静止しており、 時空原点に存在する ＋ｑ１ の電荷量はＸ軸方向に、 速さ ｖ１ で等速直線運動しています。
このとき、 時空原点には、 Ｘ軸方向に
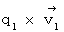の大きさの 相対的空間電気量 が生じていると言うことができます。 一方、 時空点Ｂ（ Ｙ軸上の ａ 目 のところ ）に電荷量 ｑ２ が存在し、 Ｘ軸方向に速さ ｖ２ で等速直線運動をしています。 時空原点の相対的空間電気量より、 光子が放たれ、 
目 後に電荷量 ｑ２ に届き、 磁力を及ぼします。図2101
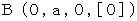
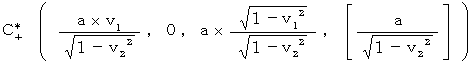
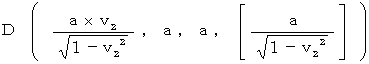
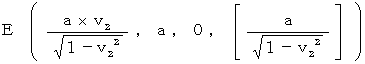
まず、 電荷量 ｑ２ が静止している座標系を考えます。
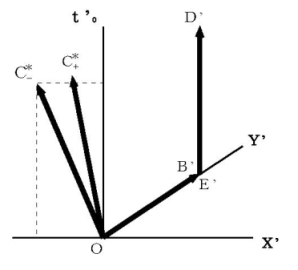
図2102 を見てください。（ 便宜上３次元空間を２次元で表しています。）
図2102
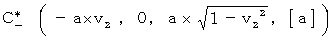
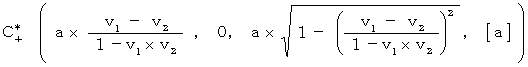
－ｑ１ の電荷は、Ｘ軸の方向に、 速さ －ｖ２ で等速直線運動しており、 ＋ｑ１ の電荷は、Ｘ軸の方向に、
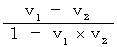で速直線運動しています。電荷 ＋ｑ１ の 電荷 －ｑ１ に対する現実的な速さは、 次の式から得られます。
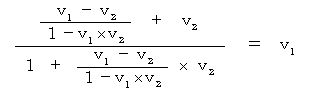
したがって、 相対的空間電気量は、 座標変換にても変化しないことがわかります。
その次に、 Ｂ’，Ｄ’，Ｅ’ が次のようであれば、 図2102 の Ｘ’Ｙ’ｔ’０ 座標系 を第１観察者の座標系としたときに、 第１観察者に対してＸ軸の負の方向に ｖ２ の速さで等速直線運動をしている第２観察者への座標変換の結果が、 図2101 の ＸＹｔ０ 座標系 になっていることがわかります。
Ｂ’（ ０， ａ， ０， ［０］ ）
Ｄ’（ ０， ａ， ａ， ［ａ］ ）
Ｅ’（ ０， ａ， ０， ［ａ］ ）
したがって、 このとき、 図2102 と 図2101 は「 運動学的同等状態 」であると言うことができます。
そこで、 図2102 において、 電荷量 ｑ２ に働く力について考えてみましょう。
時空原点の相対的空間電気量が、 時空点 Ｄ’ に作る磁場は、 方向がＺ軸方向で、 大きさが
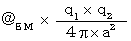です。なぜなら、 磁場（
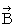）は次の式で定義されるからです。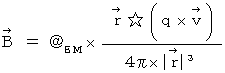
しかし、 静止している電荷量 ｑ２ は、 空間電気量が ０ なので、 磁場の影響を受けません。 静止している電荷量 ｑ２ が影響を受けるのは、 仮想電場です。
では、 時空点 Ｄ’ に形成される仮想電場について考えましょう。 それは、 時空点 Ｄ’ に存在する移動している磁場によって産生されます。
時空点 Ｄ’ に存在する磁場の運動速度は、 それの生みの親であるところの時空原点に存在する 相対的空間電気量
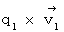を形作る負の電荷量の運動速度に等しいので、 大きさが ｖ２ で、 方向がＸ軸の負の方向になります。よって 、仮想電場の法則 ：
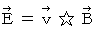より、 時空点 Ｄ ’ に形成される仮想電場（ 
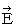）は、 方向がＹ軸の負の方向で、 大きさが 
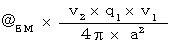です。よって、 電荷間電気力の場的表現：
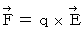より、 電荷量 ｑ２ に働く力の大きさは、 
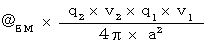になり、 方向は、 Ｙ軸の負の方向になります。最後に、 図2102 と 図2101 は「 運動学的同等状態 」であるので、 図2101 での電荷量 ｑ２ に働く力は、 図2102 での電荷量 ｑ２ に働く力に等しく、 図2101 で電荷量 ｑ２ に働く 電荷間磁気力（ 相対的空間電気量が空間電気量に及ぼす力 ）は、
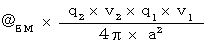になり、 方向は、 Ｙ軸の負の方向になります。