��Q�Q�́@�@�d��Ǝ���̓���
�i�P�j�Q�̓d�חʂ̊Ԃɓ����͂̍��W�ϊ�
�@ ��ʓI�ȒP�ʌn�i �r�h �P�ʌn �j�ɂ����ẮA ��ʓI�Ɏ������x�A ����A �d��͎��̎��ŕ\����܂��B
�@�@�@�@�������x �F
�@�@�@�@�@�@�@�@�@�@�@
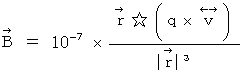
�@�@�@�@���� �F
�@�@�@�@�@�@�@�@�@�@�@
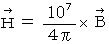
�@�@�@�@�d�� �F
�@�@�@�@�@�@�@�@�@�@�@
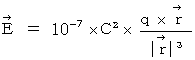
�������x �� �d�� ���A �ځE�H�E�c �P�ʌn �ŕ\���܂��ƁA ���̂悤�ɂȂ�܂��B
�@�@�@�@�������x �F
�@�@�@�@�@�@�@�@�@�@�@
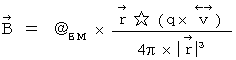 �@�@�@�@�@���@
�@�@�@�@�@���@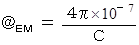
�@�@�@�@�d�� �F
�@�@�@�@�@�@�@�@�@�@�@
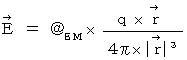
�@ ���̊����n���ΐ����_�ł́A ���̂悤�ȁu �������� �v�Ɓu �����d�� �v��d����Ƃ��ėp���܂��B �����́A �ځE�H�E�c �P�ʌn ��p���āA ���̂悤�ɕ\����܂��B
�@�@�@�������� �F�@�i ���́A �������x�̂��Ƃ��u �������� �v�ƌ����Ă��܂��B�j
�@�@�@�@�@�@�@�@�@�@�@
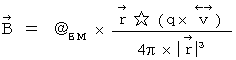
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����āA ���[�����c�͎͂��̎��ŕ\����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
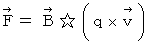
�@�@�@�����d�� �F�@�i ���́A �d������̑����Ŋ��������̂��u �����d�� �v�ƌ����Ă��܂��B�j
�@�@�@�@�@�@�@�@�@�@�@
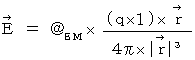
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����āA �N�[�����͎͂��̎��ŕ\����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
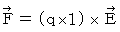
�@ ���ꂩ��A �������x�ňړ����Ă���Q�̓d�חʂ̊Ԃɓ����͂̍��W�ϊ��ɂ��čl���Ă݂܂��傤�B
�@ ��P�ώ@�҂̋�Ԍ��_
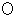 �ɂ́A ��Ύ��_
�ɂ́A ��Ύ��_  �̂Ƃ��A �d�ח�
�̂Ƃ��A �d�ח� 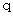 ���������`������A �w���̐��̕����ɑ���
���������`������A �w���̐��̕����ɑ���  �œ��������^�����Ă��܂��B ��P�ώ@�҂̂S��������ԍ��W�n�̎���_
�œ��������^�����Ă��܂��B ��P�ώ@�҂̂S��������ԍ��W�n�̎���_  �ɂ����� �����d�� �� �������� �����̂悤�ɕ\���܂��B �����̓d����́A �����`�ȊO�̂��̂ɂ���Ă͍���Ȃ��Ƃ��܂��B
�ɂ����� �����d�� �� �������� �����̂悤�ɕ\���܂��B �����̓d����́A �����`�ȊO�̂��̂ɂ���Ă͍���Ȃ��Ƃ��܂��B�@�@�@�@�@
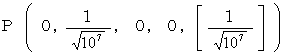
�@�@�@�@�@�����d�� �F�@
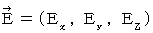 �@�C�@�@�@�������� �F�@
�@�C�@�@�@�������� �F�@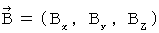
�@ �܂��A ��P�ώ@�҂̂S��������ԍ��W�n�̎���_
 �ɂ͓d�ח�
�ɂ͓d�ח� 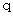 ���������a�����݂��Ă���A ����͂w���̐��̕����ɑ���
���������a�����݂��Ă���A ����͂w���̐��̕����ɑ���  �œ��������^�����Ă��܂��B
�œ��������^�����Ă��܂��B�@ ��P�ώ@�҂ɂƂ��Ă̕����`�╨���a�̋�ԑ��x���@
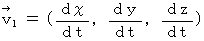 �@�ŕ\���ƁA�@
�@�ŕ\���ƁA�@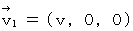 �@�ɂȂ�܂��B
�@�ɂȂ�܂��B�@ �܂��A ����_
 �̋�Ԍ��_����̋�Ԉʒu�x�N�g���͎��̂悤�ɂȂ�܂��B
�̋�Ԍ��_����̋�Ԉʒu�x�N�g���͎��̂悤�ɂȂ�܂��B�@�@�@�@�@
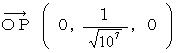
�@ ��P�ώ@�҂̍��W�n�ł́A �����`�̎��u ���ΓI��ԓd�C�� �v�̑傫����
 �ŁA �����a�̎��u ��ԓd�C�� �v�̑傫����
�ŁA �����a�̎��u ��ԓd�C�� �v�̑傫���� 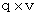 �ł��B
�ł��B�@ ����ɁA ��P�ώ@�҂ɑ��āA �w���̐��̕����ɑ���
 �œ��������^�����Ă����O�ώ@�҂����܂��B �Q�l�̎��_�͈�v���Ă��܂��B ��O�ώ@�҂̂S��������ԍ��W�n�̎���_
�œ��������^�����Ă����O�ώ@�҂����܂��B �Q�l�̎��_�͈�v���Ă��܂��B ��O�ώ@�҂̂S��������ԍ��W�n�̎���_ 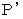 �ɂ����� �����d�� �� �������� �����̂悤�ɕ\���܂��B
�ɂ����� �����d�� �� �������� �����̂悤�ɕ\���܂��B�@�@�@�@�@
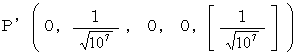
�@�@�@�@�@�����d�� �F�@
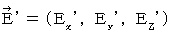 �@�C�@�@�@�������� �F�@
�@�C�@�@�@�������� �F�@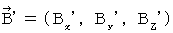
�@ ���̂Ƃ��A ��O�ώ@�҂̋�Ԍ��_�ɂ͕����`���Î~���Ă���A ��O�ώ@�҂̂S��������ԍ��W�n�̎���_
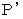 �ɂ͐Î~���Ă��镨���a�����݂��Ă��邱�ƂɂȂ�܂��B
�ɂ͐Î~���Ă��镨���a�����݂��Ă��邱�ƂɂȂ�܂��B�@ ��O�ώ@�҂ɂƂ��Ă̕����`�╨���a�̋�ԑ��x���@
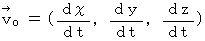 �@�ŕ\���ƁA�@
�@�ŕ\���ƁA�@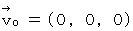 �@�ɂȂ�܂��B
�@�ɂȂ�܂��B�@ �܂��A ����_
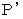 �̋�Ԍ��_����̋�Ԉʒu�x�N�g���͎��̂悤�ɂȂ�܂��B
�̋�Ԍ��_����̋�Ԉʒu�x�N�g���͎��̂悤�ɂȂ�܂��B�@�@�@�@�@
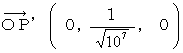
�@ ��O�ώ@�҂̍��W�n�ł́A �����`�̎��u ���ΓI��ԓd�C�� �v�̑傫����
 �ŁA �����a�̎��u ��ԓd�C�� �v�̑傫����
�ŁA �����a�̎��u ��ԓd�C�� �v�̑傫����  �ł��B
�ł��B�@ �ł́A ��P�ώ@�҂̍��W�n�ɂ����āA �����`�������a�ɋy�ڂ��d���C�I�ȗ͂����߂Ă݂܂��傤�B
�@ �܂��A ��P�ώ@�҂̎���_
 �ɂ���������d��i
�ɂ���������d��i 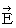 �j�����߂܂��B
�j�����߂܂��B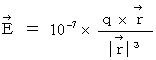 �@�ł���A�@�@
�@�ł���A�@�@ �@�̂Ƃ�
�@�̂Ƃ�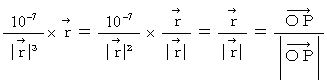 �@�ł�����A
�@�ł�����A 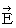 �͎��̂悤�ɂȂ�܂��B
�͎��̂悤�ɂȂ�܂��B�@�@�@�@�@
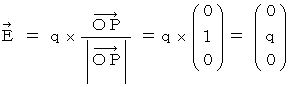
���������āA �����`�������a�ɋy�ڂ��N�[������
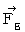 �́A ���̂悤�ɂȂ�܂��B
�́A ���̂悤�ɂȂ�܂��B�@�@�@�@�@
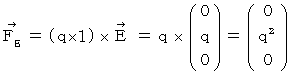
�@ ���ɁA ��P�ώ@�҂̎���_
 �ɂ������������i
�ɂ������������i 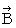 �j��
�j��  �ł��B �Ȃ��Ȃ�A ��������̂́A�u ��ԓd�C�� �v�ł͂Ȃ��A�u ���ΓI��ԓd�C�� �v������ł��B ���������āA ��P�ώ@�҂ɂƂ��āA �����`�������a�ɋy�ڂ����[�����c��
�ł��B �Ȃ��Ȃ�A ��������̂́A�u ��ԓd�C�� �v�ł͂Ȃ��A�u ���ΓI��ԓd�C�� �v������ł��B ���������āA ��P�ώ@�҂ɂƂ��āA �����`�������a�ɋy�ڂ����[�����c�� 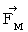 ��
��  �ł��B
�ł��B�@ ���������āA ��P�ώ@�҂ɂƂ��āA �����`�������a�ɋy�ڂ��d���C�w�I�ȗ�
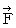 �́A ���̂悤�ɂȂ�܂��B
�́A ���̂悤�ɂȂ�܂��B�@�@�@�@�@
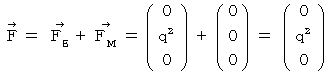
�@ �����āA ��O�ώ@�҂̍��W�n�ɂ����āA �����`�������a�ɋy�ڂ��d���C�I�ȗ͂����߂Ă݂܂��傤�B
�@ �܂��A ��O�ώ@�҂̎���_
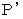 �ɂ���������d��i
�ɂ���������d��i 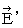 �j�����߂܂��B
�j�����߂܂��B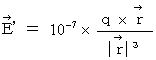 �@�ł���A�@�@
�@�ł���A�@�@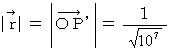 �@�̂Ƃ�
�@�̂Ƃ�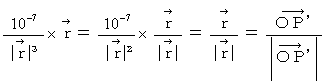 �@�ł�����A
�@�ł�����A 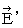 �͎��̂悤�ɂȂ�܂��B
�͎��̂悤�ɂȂ�܂��B�@�@�@�@�@
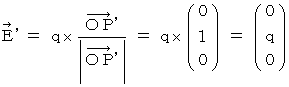
���������āA �����`�������a�ɋy�ڂ��N�[�����́i
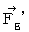 �j�́A ���̂悤�ɂȂ�܂��B
�j�́A ���̂悤�ɂȂ�܂��B�@�@�@�@�@
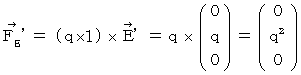
�@ ���ɁA ��O�ώ@�҂̎���_
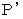 �ɂ������������i
�ɂ������������i 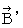 �j��
�j��  �ł��B ���������āA �����`�������a�ɋy�ڂ����[�����c�́i
�ł��B ���������āA �����`�������a�ɋy�ڂ����[�����c�́i 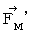 �j��
�j��  �ł��B
�ł��B�@ ���������āA��O�ώ@�҂ɂƂ��āA �����`�������a�ɋy�ڂ��d���C�w�I�ȗ́i
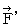 �j�́A ���̂悤�ɂȂ�܂��B
�j�́A ���̂悤�ɂȂ�܂��B�@�@�@�@�@
�@ ���������킯�ŁA ��P�ώ@�҂̍��W�n�Ƒ�O�ώ@�҂̍��W�n�ƂŁA �����`�������a�ɋy�ڂ��d���C�w�I�ȗ͂��������Ȃ��Ă���A ���ΐ��������������Ă��邱�Ƃ��킩��܂��B
�@ ���ɁA ���̏ɉ����āA ��P�ώ@�҂̋�Ԍ��_
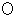 �ɁA �d�ח�
�ɁA �d�ח� 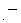
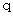 ���������b���Î~���Ă���ꍇ�ɂ��čl���Ă݂܂��傤�B ���x�́A �����`�ƕ����b�Ƃ������a�̑��݂����_�ɓd��⎥�����邱�ƂɂȂ�܂��B
���������b���Î~���Ă���ꍇ�ɂ��čl���Ă݂܂��傤�B ���x�́A �����`�ƕ����b�Ƃ������a�̑��݂����_�ɓd��⎥�����邱�ƂɂȂ�܂��B�@ �܂����̏ꍇ�́A ��P�ώ@�҂̍��W�n�ł́A �����`�̎��u ���ΓI��ԓd�C�� �v�̑傫����
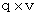 �ŁA �����a�̎��u ��ԓd�C�� �v�̑傫����
�ŁA �����a�̎��u ��ԓd�C�� �v�̑傫���� 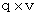 �ɂȂ�܂��B �܂��A ��O�ώ@�҂̍��W�n�ł́A �����`�̎��u ���ΓI��ԓd�C�� �v�̑傫����
�ɂȂ�܂��B �܂��A ��O�ώ@�҂̍��W�n�ł́A �����`�̎��u ���ΓI��ԓd�C�� �v�̑傫���� 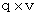 �ŁA �����a�̎��u ��ԓd�C�� �v�̑傫����
�ŁA �����a�̎��u ��ԓd�C�� �v�̑傫����  �ɂȂ�܂��B
�ɂȂ�܂��B�@ �ł́A ��P�ώ@�҂̍��W�n�ɂ����āA �����`�ƕ����b�Ƃ������a�ɋy�ڂ��d���C�I�ȗ͂����߂Ă݂܂��傤�B
�@ �܂��A ��P�ώ@�҂̎���_
 �ɂ���������d��i
�ɂ���������d��i 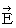 �j��
�j��  �ł��B ���������āA �����`�ƕ����b�Ƃ������a�ɋy�ڂ��N�[������
�ł��B ���������āA �����`�ƕ����b�Ƃ������a�ɋy�ڂ��N�[������ 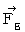 ��
��  �ł��B
�ł��B�@ ���ɁA ��P�ώ@�҂̎���_
 �ɂ������������i
�ɂ������������i 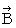 �j�����߂܂��B
�j�����߂܂��B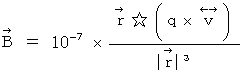 �@�ł���A�@�@
�@�ł���A�@�@ �@�̂Ƃ�
�@�̂Ƃ�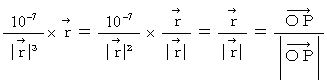 �@�ł�����A
�@�ł�����A 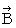 �͎��̂悤�ɂȂ�܂��B
�͎��̂悤�ɂȂ�܂��B�@�@�@�@�@
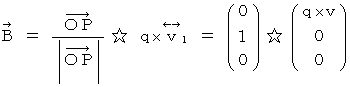
�@ ���āA
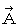 �ɑ���
�ɑ��� 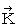 ���O�ς�����Ƃ������Z
���O�ς�����Ƃ������Z 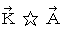 �́A ��ʂ̊O�ςł�
�́A ��ʂ̊O�ςł� 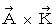 �ŕ\����܂����A ����́A ���̂悤�ȃx�N�g���̐�������Ȃ�s��̐ςŕ\����܂��B
�ŕ\����܂����A ����́A ���̂悤�ȃx�N�g���̐�������Ȃ�s��̐ςŕ\����܂��B�@�@�@�@�@
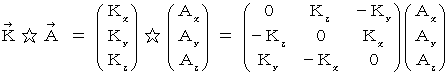
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@

�����p���Ď����d������߂�ƁA ���̂悤�ɂȂ�܂��B
�@�@�@�@�@
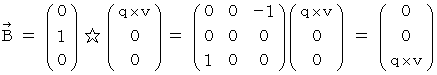
���������āA �����`�ƕ����b�Ƃ������a�ɋy�ڂ����[�����c�́i
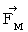 �j�́A ���̂悤�ɂȂ�܂��B
�j�́A ���̂悤�ɂȂ�܂��B�@�@�@�@�@
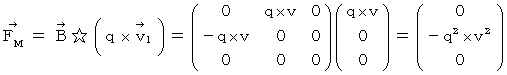
�@ ���������āA ��P�ώ@�҂ɂƂ��āA �����`�ƕ����b�Ƃ������a�ɋy�ڂ��d���C�w�I�ȗ�
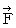 �́A ���̂悤�ɂȂ�܂��B
�́A ���̂悤�ɂȂ�܂��B�@�@�@�@�@
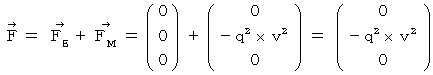
�@ �����āA ��O�ώ@�҂̍��W�n�ɂ����āA �����`�ƕ����b�Ƃ������a�ɋy�ڂ��d���C�I�ȗ͂����߂Ă݂܂��傤�B
�@ �܂��A ��O�ώ@�҂̎���_
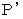 �ɂ���������d��i
�ɂ���������d��i 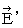 �j��
�j��  �ł��B ���������āA �����`�ƕ����b�Ƃ������a�ɋy�ڂ��N�[�����́i
�ł��B ���������āA �����`�ƕ����b�Ƃ������a�ɋy�ڂ��N�[�����́i 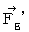 �j��
�j��  �ł��B
�ł��B�@ ���ɁA ��O�ώ@�҂̎���_
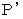 �ɂ������������i
�ɂ������������i 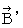 �j�����߂܂��B
�j�����߂܂��B�@�@�@�@�@
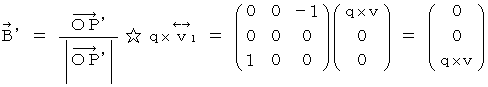
�@ ���������āA �����`�ƕ����b�Ƃ������a�ɋy�ڂ����[�����c�́i
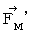 �j�́A ���̂悤�ɂȂ�܂��B
�j�́A ���̂悤�ɂȂ�܂��B�@�@�@�@�@
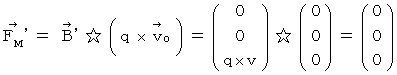
�@ ���āA �����ŖY��ĂȂ�Ȃ��̂́A�u ���z�d�� �v�̑��݂ł��B ����_
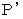 �Ɍ`�����ꂽ��������i
�Ɍ`�����ꂽ��������i 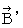 �j�́A �Ԏ��̕��̕����ɑ���
�j�́A �Ԏ��̕��̕����ɑ���  �ŁA �ړ����Ă��܂��B �Ȃ��Ȃ�A ���̑��x�́A ���̎�������̎Y�݂̐e�ł���Ƃ���́u ���ΓI��ԓd�C�� �v���`�����Ă��镉�̓d�חʂ̑��x�ɓ���������ł��B �܂�A �����b�̑��x�ɓ���������ł��B ���������āA ����_
�ŁA �ړ����Ă��܂��B �Ȃ��Ȃ�A ���̑��x�́A ���̎�������̎Y�݂̐e�ł���Ƃ���́u ���ΓI��ԓd�C�� �v���`�����Ă��镉�̓d�חʂ̑��x�ɓ���������ł��B �܂�A �����b�̑��x�ɓ���������ł��B ���������āA ����_ 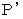 �ɂ͎��̂悤�ȉ��z�d��i
�ɂ͎��̂悤�ȉ��z�d��i 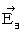 �j���`������Ă��܂��B
�j���`������Ă��܂��B�@�@�@�@�@
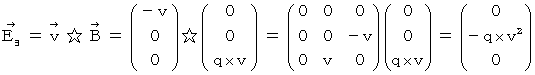
���������āA ���z�d��ɂ�蕨���a����́i
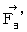 �j�͎��̂悤�ɂȂ�܂��B
�j�͎��̂悤�ɂȂ�܂��B�@�@�@�@�@
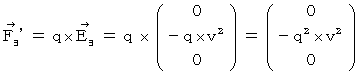
�@ ���������āA��O�ώ@�҂ɂƂ��āA �����`�ƕ����b�Ƃ������a�ɋy�ڂ��d���C�w�I�ȗ́i
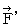 �j�́A ���̂悤�ɂȂ�܂��B
�j�́A ���̂悤�ɂȂ�܂��B�@�@�@�@�@
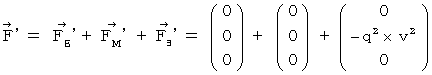
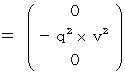
�@ ���������킯�ŁA ���̏ꍇ���A ��P�ώ@�҂̍��W�n�Ƒ�O�ώ@�҂̍��W�n�ƂŁA �����`�ƕ����b�������a�ɋy�ڂ��d���C�w�I�ȗ͂��������Ȃ��Ă���A ���ΐ��������������Ă��邱�Ƃ��킩��܂��B
�i�Q�j���s�ɏI������u �d��Ǝ���̊��S���� �v�ւ̎���
�@ �����d���g�̈��ł��邱�Ƃ������t�@���f�B�[�̍l����������ɔ��W�����āA ���̂悤�Ɍ������Ƃ͂ł��Ȃ��ł��傤���H
�@ �@�@�u�@�d��Ǝ���͓d����Ƃ����������̂̕ʁX�̌`�Ԃɂ����Ȃ��B �d��Ǝ���́A
�@�@�@�@�S�����������ʂł���A �ώ@�̂�����ɂ���āA �ǂ��炩�̐�߂銄�����傫��
�@�@�@�@�����Ă���Ƃ����悤�Ȃ��̂ł���B�v
�@ �����ŁA�u ���q�̓d����I�U���̖@�� �v�����̂悤�ɕύX���Ă݂܂��B �Ȃ��Ȃ�A ���̂ق������R�Ȋ��������邩��ł��B
�@�@�@�@�u�@�d�חʂ����������̌��q�̓d����I�U���́A �ǂ�Ȋώ@�̂����������
�@�@�@�@ ���A �P�ʐ�Ύ��Ԃ�����̐U�����A �܂�A ���q�̓d����I�U���̑����i �d
�@�@�@�@ �ח� �j�͈��ł���A ���̐U���� ��Ԑ��� �� ���Ύ��Ԑ��� �ɕ�������āA
�@�@�@�@ ���ꂼ�ꂪ��Ԃ𑬂�
 �œ`����Ă����B�@ �O�҂́A ������`�����ă��[����
�œ`����Ă����B�@ �O�҂́A ������`�����ă��[�����@�@�@�@ �c�͂݁A ��҂́A �d����`�����ăN�[�����͂ށB�v
�@ ����ƁA �N�[�����̖@���͎��̂悤�ɏ���������܂��B
�@�@�@�@
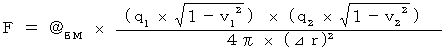
�@ �܂�A �d��ނ̂́A�u �S��������ԓd�C�� �v�ł͂Ȃ��A�u ���Ύ��ԓd�C�� �v�ł���Ƃ���̂ł��B
�@ ����ƁA�u �����d�� �v�� �N�[�����͂́A ���ꂼ�ꎟ�̂悤�ɕ\����܂��B
�@�@�@�@�@
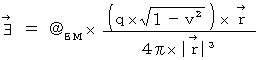
�@�@�@�@�@
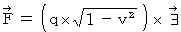
�@ �܂��A ����ނ̂́A�u ���ΓI��ԓd�C�� �v�ł͂Ȃ��A�u ��ԓd�C�� �v�ł���Ƃ��܂��B �Ȃ��Ȃ�A ���̂ق������R�Ȋ��������邩��ł��B ����ƁA ���̂悤�ɂȂ�܂��B
�@�@�@�@�@
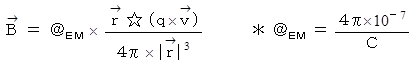
�@ ���ꂩ��A ��قǍl�����悤�ɁA �������x�ňړ����Ă���Q�̓d�חʂ̊Ԃɓ����͂̍��W�ϊ����l���Ă݂܂��傤�B
�@ �ݒ�͐�قǂ̍ŏ��ƑS�������ɂ��܂��B�i �����b�͑��݂��܂���B�j����ƁA ��P�ώ@�҂̍��W�n�ł́A �����`�̎��u ���Ύ��ԓd�C�� �v�̑傫����
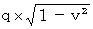 �ł���A �����a�̎��u ��ԓd�C�� �v�̑傫����
�ł���A �����a�̎��u ��ԓd�C�� �v�̑傫���� 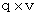 �ɂȂ�܂��B �܂��A ��O�ώ@�҂̍��W�n�ł́A �����`�̎��u ���Ύ��ԓd�C�� �v�̑傫����
�ɂȂ�܂��B �܂��A ��O�ώ@�҂̍��W�n�ł́A �����`�̎��u ���Ύ��ԓd�C�� �v�̑傫���� 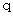 �ł���A �����a�̎��u ��ԓd�C�� �v�̑傫����
�ł���A �����a�̎��u ��ԓd�C�� �v�̑傫����  �ɂȂ�܂��B
�ɂȂ�܂��B�@ �ł́A ��P�ώ@�҂̍��W�n�ɂ����āA �����`�������a�ɋy�ڂ��d���C�I�ȗ͂����߂Ă݂܂��傤�B
�@ �܂��A ��P�ώ@�҂̎���_
 �ɂ���������d��i
�ɂ���������d��i 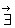 �j�����߂܂��B
�j�����߂܂��B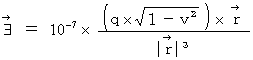 �@�ł���A�@�@
�@�ł���A�@�@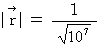 �@�̂Ƃ��A
�@�̂Ƃ��A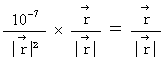 �@�ł�����A�@
�@�ł�����A�@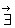 �͎��̂悤�ɂȂ�܂��B
�͎��̂悤�ɂȂ�܂��B�@�@�@�@�@
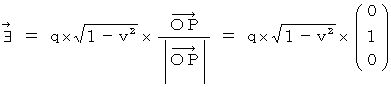
�@�@�@�@�@
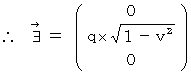
�@ ���ɁA ��P�ώ@�҂̎���_
 �ɂ������������i
�ɂ������������i 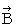 �j�����߂܂��B
�j�����߂܂��B�@�@�@�@�@
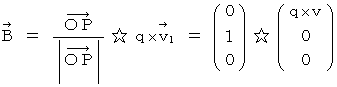
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
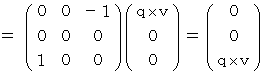
�@ ���āA�u �S��������ԓd�C��
 �v�Ɂu �d����e���\��
�v�Ɂu �d����e���\��  �v����p�����邱�Ƃɂ���āA�u �S�����d���C��
�v����p�����邱�Ƃɂ���āA�u �S�����d���C��  �v�邱�Ƃ��ł��܂��B
�v�邱�Ƃ��ł��܂��B�@�@�@�@
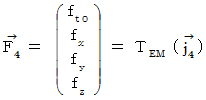
�@�@�@�@
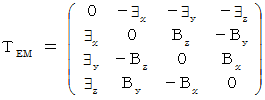
�@�@�@�@
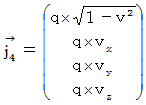
�@�@�@�@�܂�A
�@�@�@�@�@�@�@�@
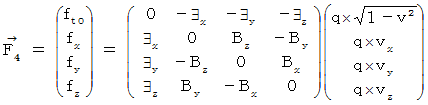
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
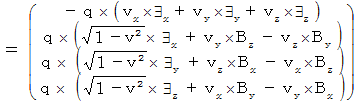
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�������A
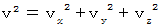
�� �R�����g�F
�@�� ���[�����c�͂́A ���̂悤�ɕ\����܂��B
�@�@�@�@�@
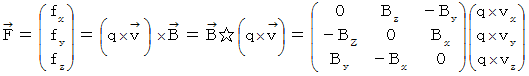
�@�@�@�@�@�@�@�@�@�@�@�@
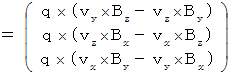
�@�� �N�[�����͂́A ���̂悤�ɕ\����܂��B
�@�@�@�@�@
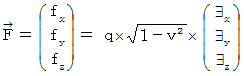
�@ �����ŁA�u ���f���d����e���\��
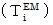 �v���Љ���Ă��������܂��B
�v���Љ���Ă��������܂��B�@�@�@�@
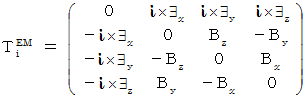
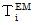 ��p����ƁA�u�S�����d���C�́i
��p����ƁA�u�S�����d���C�́i 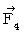 �j�v�́A ���̂悤�ɂȂ�܂��B
�j�v�́A ���̂悤�ɂȂ�܂��B�@�@�@�@
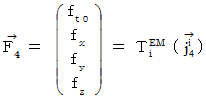
�@�@�@�@�@�@�@�@�@�@�������A�@
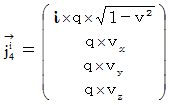
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���́A
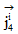 ���u ���f���S�����d�C�� �v�ƌ����Ă��܂��B
���u ���f���S�����d�C�� �v�ƌ����Ă��܂��B�@�@�@�@�܂�A
�@�@�@�@�@�@�@�@
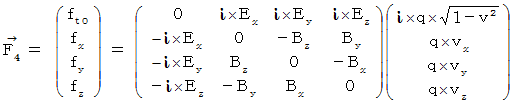
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
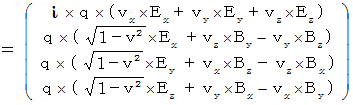
�@ �ł́A ���ɖ߂��āA ��P�ώ@�҂ɂƂ��Ă̕����`�������a�ɋy�ڂ��d���C�I�ȗ͂����߂Ă݂܂��傤�B ��P�ώ@�҂̍��W�n�ɂ����āA �����`�������a�ɋy�ڂ��u�S�����d���C�́i
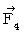 �j�v�́A �S��������ԓd�C�ʂ��d����e���\������p�����āA ���̂悤�ɂȂ�܂��B
�j�v�́A �S��������ԓd�C�ʂ��d����e���\������p�����āA ���̂悤�ɂȂ�܂��B�@�@�@�@
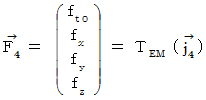
�@�@�@�@�@�@
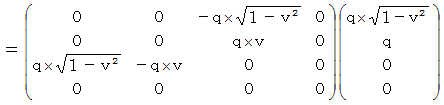
�@�@�@�@�@�@
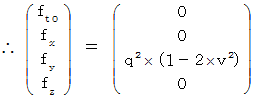
�@ �����āA ��O�ώ@�҂̍��W�n�ɂ����āA �����`�������a�ɋy�ڂ��d���C�I�ȗ͂����߂Ă݂܂��傤�B
�@ �܂��A ��O�ώ@�҂̎���_
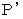 �ɂ���������d��i
�ɂ���������d��i 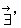 �j�����߂܂��B ��قǂƓ����ł��B
�j�����߂܂��B ��قǂƓ����ł��B�@�@�@�@�@
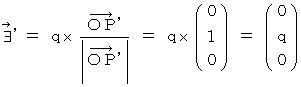
�@ ���ɁA ��O�ώ@�҂̎���_
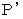 �ɂ������������i
�ɂ������������i 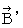 �j��
�j��  �ł��B
�ł��B�@ ���������āA �����`�������a�ɋy�ڂ��u �S�����d���C��
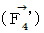 �v�́A ���̂悤�ɂȂ�܂��B
�v�́A ���̂悤�ɂȂ�܂��B�@�@�@�@
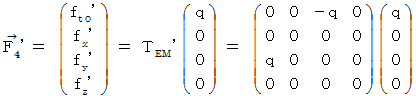
�@�@�@�@�@�@�@
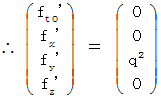
�@ ���������āA
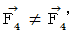 �@�ł��B �܂�A ��P�ώ@�҂̍��W�n�Ƒ�O�ώ@�҂̍��W�n�Ƃł́A �����`�������a�ɋy�ڂ��� ���قȂ�܂��B �{���́A ��P�ώ@�҂ɂƂ��Ă���O�ώ@�҂ɂƂ��Ă��A �����`�������a�ɋy�ڂ��d���C�I�ȗ͓͂������āA ���ΐ����������藧���Ă��邱�Ƃ����҂��āA ��قǂ̉���������̂ł����A �c�O�Ȃ���v���悤�ɂȂ�܂���ł����B �����A ���������ɓd��������Ă��铱���̊Ԃɐ˗͂����������̂ł�����A ���܂������̂ł����A �c�O�I �����͂��̔��̈��͂Ȃ̂ł��B
�@�ł��B �܂�A ��P�ώ@�҂̍��W�n�Ƒ�O�ώ@�҂̍��W�n�Ƃł́A �����`�������a�ɋy�ڂ��� ���قȂ�܂��B �{���́A ��P�ώ@�҂ɂƂ��Ă���O�ώ@�҂ɂƂ��Ă��A �����`�������a�ɋy�ڂ��d���C�I�ȗ͓͂������āA ���ΐ����������藧���Ă��邱�Ƃ����҂��āA ��قǂ̉���������̂ł����A �c�O�Ȃ���v���悤�ɂȂ�܂���ł����B �����A ���������ɓd��������Ă��铱���̊Ԃɐ˗͂����������̂ł�����A ���܂������̂ł����A �c�O�I �����͂��̔��̈��͂Ȃ̂ł��B�@ �����ŁA�u ���f���d����e���\��
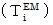 �v�̏o�Ԃł��B ������g���āA
�v�̏o�Ԃł��B ������g���āA 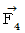 ��
�� 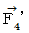 �����߂Ă݂܂��傤�B
�����߂Ă݂܂��傤�B�@�@�@�@
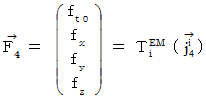
�@�@�@�@�@�@�@
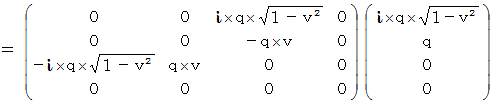
�@�@�@�@�@�@�@
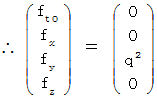
�@�@�@�@
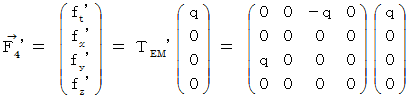
�@�@�@�@�@�@�@
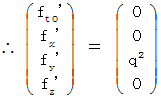
�@ ���������āA
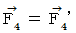 �@���@
�@���@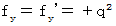 �@�ł��B ����ŁA �������肵�܂����ˁB �������A ���́A �u �������Ԃ��̗p���Ă���~���R�t�X�L�[����� �v�͌����̂��̂ł͂Ȃ��A �����w�������ׂ����̂ł͂Ȃ� �ƍl���܂��̂ŁA�u ���f���d����e���\�� �v��p���Ă��������ł��Ȃ������͊ԈႢ�ł���Ǝv���܂��B �����ŁA ���̏͂́i�Q�j�̉����͂��ׂċp�����邱�Ƃɂ��܂��B
�@�ł��B ����ŁA �������肵�܂����ˁB �������A ���́A �u �������Ԃ��̗p���Ă���~���R�t�X�L�[����� �v�͌����̂��̂ł͂Ȃ��A �����w�������ׂ����̂ł͂Ȃ� �ƍl���܂��̂ŁA�u ���f���d����e���\�� �v��p���Ă��������ł��Ȃ������͊ԈႢ�ł���Ǝv���܂��B �����ŁA ���̏͂́i�Q�j�̉����͂��ׂċp�����邱�Ƃɂ��܂��B�i�R�j�}�N�X�E�F���������ɔ�߂�ꂽ���f���d����̓�
�@ �~���R�t�X�L�[��Ԃɂ͓d���ꂪ�`������Ă���Ƃ��܂��B ����ƁA ����Ԃ��ړ����Ă���d�חʂ́u �S�����d�� �v���`�����܂��̂ŁA ���̓d�חʂɂ͓d����ɂ��u �S������ �v����p���܂��B ���鎞��_�ɂ�����d�����\���̂��u ���f���d����e���\��
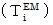 �v�ł��B�u ���f���d����e���\�� �v�́A �U�̐������琬��S�s�S��̔��Ώ̍s��ŕ\����܂��B
�v�ł��B�u ���f���d����e���\�� �v�́A �U�̐������琬��S�s�S��̔��Ώ̍s��ŕ\����܂��B�@�@�@�@
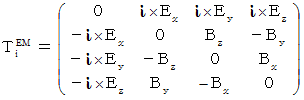
�@ �@�@�@�@�@�@�@�@�@�@�@�@�@���@
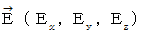 �͎����d��ł��B �����d��͓d������̑�
�͎����d��ł��B �����d��͓d������̑��@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���Ŋ��������̂ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�ڍH�c�P�ʌn�ł́A �����d��͓d��Ɠ����ł��B
�@�u ���f���d����e���\�� �v���u ���f���S�����d�� �v�ɍ�p������ƁA�u ���f���S������ �v�������܂��B ����͎��̐��`�x�N�g�������ŕ\����܂��B
�@�@�@�@
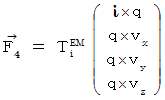
�@ �}�b�N�X�E�F���̕������́A�u ���f���d����e���\�� �v�̊e�����̊W�������Ă���ƂƂ��ɁA ���̂��Ƃ��߂Ă��܂��B
�@�u �~���R�t�X�L�[�S��������Ԃɂ����āA ���f���d����e���\�� ��Δ�������ƁA ���f���S��������ԓd�C�ʖ��x �� ���d���� �����������̂� ������B�v
�@ ���ꂩ��A ���̂��Ƃɂ��Đ������܂��B
�u ���f���d����e���\��
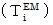 �v���A ������p���Ď��̂悤�ɕ\���܂��B
�v���A ������p���Ď��̂悤�ɕ\���܂��B�@�@�@�@
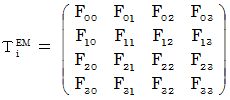
�܂��A �S��������ԍ��W
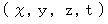 �����̂悤��
�����̂悤�� 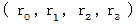 �ŕ\���܂��B
�ŕ\���܂��B�@�@�@�@
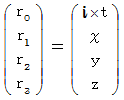
�@ ���ꂩ��A �}�N�X�E�F���̕��������A ���f���d����e���\���̐��� �� �S��������ԍ��W
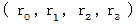 �ŕ\���Ă݂邱�Ƃɂ��܂��B
�ŕ\���Ă݂邱�Ƃɂ��܂��B�}�N�X�E�F���̕������i �ڍH�c�P�ʌn �j�F
�@�@�@�@�@�y �T �� �z�@�@
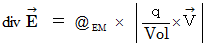
�@�@�@�@�@�y �U �� �z�@�@
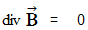
�@�@�@�@�@�y �V �� �z�@�@
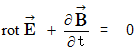
�@�@�@�@�@�y �W �� �z�@�@
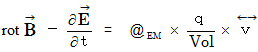
�@ �܂��A �}�N�X�E�F���̕����������Z�q�L����p���Ȃ��ŕ\���ƁA ���̂悤�ɂȂ�܂��B
�y �T �� �z
�@�@�@�@
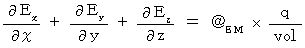 �@�@�@�@�@�@�E �E �E �E �E�i��001�j
�@�@�@�@�@�@�E �E �E �E �E�i��001�j�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���@
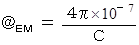
�y �U �� �z
�@�@�@�@
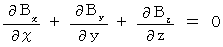 �@�@�@�@�@�@�@�@�@�@�@�E �E �E �E �E�i��002�j
�@�@�@�@�@�@�@�@�@�@�@�E �E �E �E �E�i��002�j�y �V �� �z
�@�@�@�@
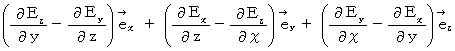
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
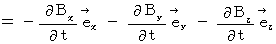
�y �W �� �z
�@�@�@
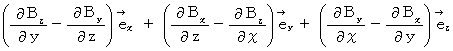
�@�@�@�@�@
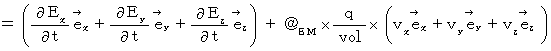
�y �V �� �z ���A
�@�@�@�@
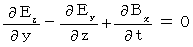 �@�@�@�@�@�E �E �E �E �E�i��003�j
�@�@�@�@�@�E �E �E �E �E�i��003�j�@�@�@�@
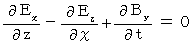 �@�@�@�@�@�E �E �E �E �E�i��004�j
�@�@�@�@�@�E �E �E �E �E�i��004�j�@�@�@�@
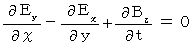 �@�@�@�@�@�E �E �E �E �E�i��005�j
�@�@�@�@�@�E �E �E �E �E�i��005�j�y �W �� �z ���A
�@�@�@�@
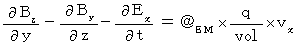 �@�@�@�@�@�E �E �E �E �E�i��006�j
�@�@�@�@�@�E �E �E �E �E�i��006�j�@�@�@�@
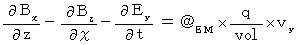 �@�@�@�@�@�E �E �E �E �E�i��007�j
�@�@�@�@�@�E �E �E �E �E�i��007�j�@�@�@�@
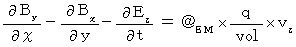 �@�@�@�@�@�E �E �E �E �E�i��008�j
�@�@�@�@�@�E �E �E �E �E�i��008�j�܂��A �y �U �� �z �� �y �V �� �z ���܂Ƃ߂Ă݂܂��B
�i��002�j���A
�@�@�@�@
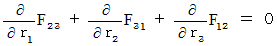 �@�@�@�@�E �E �E �E�i��002'�j
�@�@�@�@�E �E �E �E�i��002'�j�i��003�j���A
�@�@�@�@
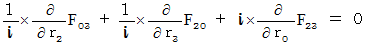
�@�@�@�@
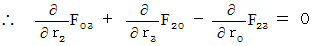
�@�@�@�@
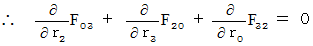
�@�@�@�@
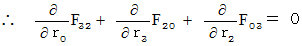 �@�@�@�@�E �E �E �E�i��003'�j
�@�@�@�@�E �E �E �E�i��003'�j�i��004�j���A
�@�@�@�@
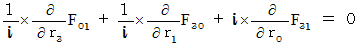
�@�@�@�@
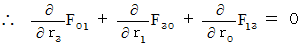
�@�@�@�@
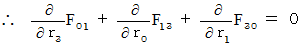 �@�@�@�@�E �E �E �E�i��004'�j
�@�@�@�@�E �E �E �E�i��004'�j�i��005�j���A
�@�@�@�@
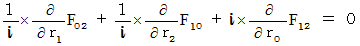
�@�@�@�@
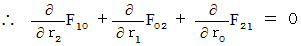 �@�@�@�@�E �E �E �E�i��005'�j
�@�@�@�@�E �E �E �E�i��005'�j�i��002'�j�`�i��005'�j�̂S�̎��́A ���̎��ɂ܂Ƃ߂邱�Ƃ��ł��܂��B
�@�@�@�@
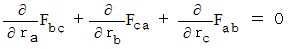
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �������A
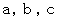 �́A ���ꂼ��قȂ� �O �` �R �̐���
�́A ���ꂼ��قȂ� �O �` �R �̐����@�@�@�@
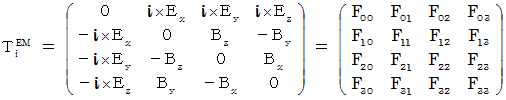
���ɁA �y �T �� �z �� �y �W �� �z ���܂Ƃ߂Ă݂܂��B
�i��001�j���A
�@�@�@�@
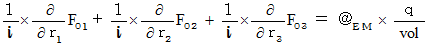
�@�@�@�@
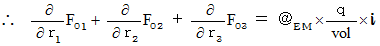 �@�@�@�@�E �E �E �E�i��001'�j
�@�@�@�@�E �E �E �E�i��001'�j�i��006�j���A
�@�@�@�@
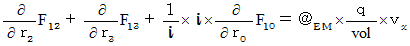
�@�@�@�@
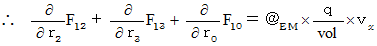
�@�@�@�@
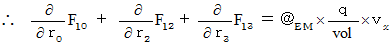 �@�@�@�@�E �E �E �E�i��006'�j
�@�@�@�@�E �E �E �E�i��006'�j�i��007�j���A
�@�@�@�@
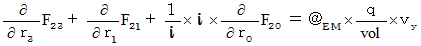
�@�@�@�@
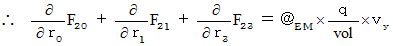 �@�@�@�@�E �E �E �E�i��007'�j
�@�@�@�@�E �E �E �E�i��007'�j�i��008�j���A
�@�@�@�@
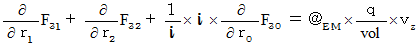
�@�@�@�@
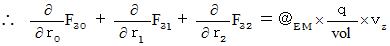 �@�@�@�@�E �E �E �E�i��008'�j
�@�@�@�@�E �E �E �E�i��008'�j�i��001'�j�Ɓi��006'�j�`�i��008'�j�̂S�̎����܂Ƃ߂ċL�q���܂��B
�@�@�@�@
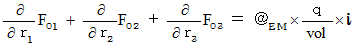
�@�@�@�@
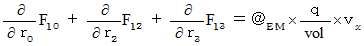
�@�@�@�@
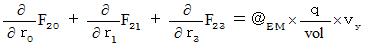
�@�@�@�@
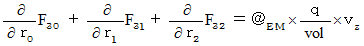
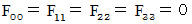 �ł�����A �����S�̎��͎��̂悤�ɂȂ�܂��B
�ł�����A �����S�̎��͎��̂悤�ɂȂ�܂��B�@�@�@�@
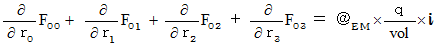
�@�@�@�@
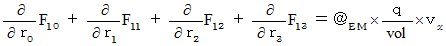
�@�@�@�@
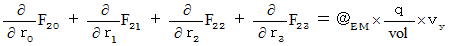
�@�@�@�@
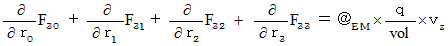
�����̂S�̎��́A ���̎��ɂ܂Ƃ߂邱�Ƃ��ł��܂��B
�@�@�@�@
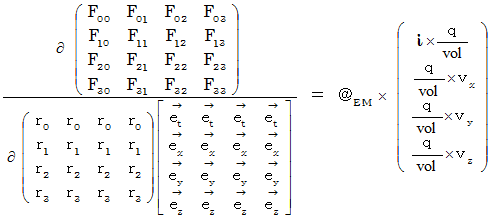
���������āA ���̎��������܂��B
�@�@�@�@
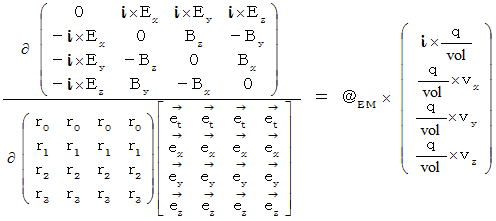
�@�@�@�@�@�@�@�@���@�R�����g�F
�@�@�@�@�@�@�@�@�@�@�@�@�@�x�N�g���F�@
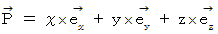 �@���A ���̂悤�ɕ\�����Ƃɂ�
�@���A ���̂悤�ɕ\�����Ƃɂ��@�@�@�@�@�@�@�@�@�@�@�@�܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
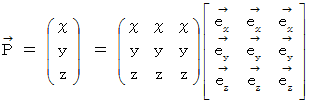
�@�@�@�@�@�@�@�@�@�@�@�@�@�e���\�����x�N�g���ŕΔ�������ƃx�N�g���������܂��B
�@ ���̎��͎��̂悤�ɕ\�����Ƃ��ł��܂��B
�@�@�@�@
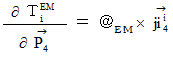
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
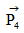 �F�@�S��������Ԉʒu�x�N�g��
�F�@�S��������Ԉʒu�x�N�g���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
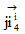 �F�@���f���S��������ԓd�C�ʖ��x
�F�@���f���S��������ԓd�C�ʖ��x�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
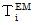 �F�@���f���d����e���\��
�F�@���f���d����e���\���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
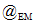 �F�@���d�����@�@
�F�@���d�����@�@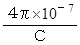
�i�S�j�d���g�̔���
�@ ���ꑊ�ΐ����_�̂Q�匴���́A�u ���ΐ����� �v�Ɓu �������s�� �v�ł���A ���ꑊ�ΐ����_�̍��{�́A�u ���[�����c�ϊ� �v�ł��B�u ���[�����c�ϊ� �v�́A �}�N�X�E�F���������ɑ���u ���ΐ����� �v�̗v�����瓱�����Ƌ��ɁA�u �������s�� �v�����������܂��B �O�҂̓��[�����c�ɂ���ĂȂ���A ��҂̓A�C���V���^�C���ɂ���ĂȂ���܂����B �����I�ɂ́A ���[�����c�̂ق������������O�ɂȂ�܂��B
�@ ���Ƃ͐l�Ԃ̎��o�ő����邱�Ƃ̂ł���d���g�ł��̂ŁA �l�Ԃ��鎩�R�̗���ɗ������w�ł́A�u �� �v�Ƃ������t���u �d���g �v�Ƃ��������w�p��ɒu���������ق����킩��₷���Ǝv���܂��B ���ꂾ���ł��A �}�N�X�E�F������������舵���Ă��� �d�� �� ���� �� �� �Ɩ��ڂȊW�ɂ��邱�Ƃ�����܂��B �S��������Ԃ��ړ����Ă���d�חʂɂ���Č`������� �d�� �� ���� �́A ���͂̋�Ԃɓ`���܂��B ���Ƃ��A��ԂɐÎ~���Ă���d�חʂ́A �d����`�����A ���ꂪ���͂̋�Ԃɓ`���܂��B ����́A �����ɂ���l�ɁA �傫�Ȑ��Œ��ڌ��t���`���̂ł͂Ȃ��āA �ׂ̐l����ׂ̐l�ւƏ����Ȑ��œ`�����Ă����ē`���̂Ɏ��Ă��܂��B �������A �d��́A ���̏ꍇ�̑����̐l�ɑ�������}�̂��Ȃ��Ƃ���Ԃ�`����Ă����܂��B �����A ���̓d�חʂ��P�U�����n�߂���A ����͓d�ꂾ���łȂ�������`�����܂����A ���̂Ƃ��A �d��⎥��͎��͂̋�Ԃɂǂ̂悤�ɓ`����Ă����̂ł��傤���H�@�`���X�s�[�h���Î~���Ă���d�חʂ��`������d��̓`��鑬���Ɠ����ł��邱�Ƃ́A �N�ɂ��z�������Ǝv���܂��B �d�חʂ��P�U������ƁA ���̐U�������ɐ����Ȃ����߂��̋�_�ł́A �������ω������������̕����ɂȂ����蕉�̕����ɂȂ����肷��d�ꂪ�`������܂��B ����ƁA ���̒P�U������d��ɂ���āA �������ω������������̕����ɂȂ����蕉�̕����ɂȂ����肷�鎥�ꂪ�`������܂��B ����ƁA ���̒P�U�����鎥��ɂ���āA �������ω������������̕����ɂȂ����蕉�̕����ɂȂ����肷��d�ꂪ�`������܂��B ���̕ω����� �d�� �� ���� �́u ������������ �v�̍�p�ɂ���Đ��܂��̂��d���g�ł��B ���̐U���́A ���ʂ̔g�̂悤�ɁA �����_�ł̈ʑ����ׂ̋�_�̈ʑ��ɏ������x��ē`���A �S�̂Ƃ��āA �d����̉��g�Ƃ��Ď��͂̋�ԂɍL�����Ă����܂��B �d���g�̓`��鑬���́A �d��⎥��̓`��鑬���Ɠ����ł��B
�@ �����d������������S��������ԂɊg�����A ���̂悤�ɕ\���܂��B
�@�@�@�@�����d�� �F�@
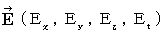 �@�@�@�@�������� �F�@
�@�@�@�@�������� �F�@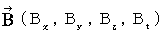
����ƁA �d�חʂ̑��݂��Ȃ���Ԃɂ����āA ���̂Q�̎������藧���܂��B
�@�@�@�@�@
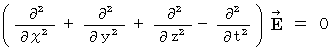 �@�@�@�@�E �E �E �E �E�i�� 22-1�j
�@�@�@�@�E �E �E �E �E�i�� 22-1�j�@�@�@�@�@
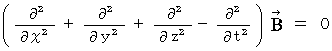 �@�@�@�@�E �E �E �E �E�i�� 22-2�j
�@�@�@�@�E �E �E �E �E�i�� 22-2�j�@ �܂����ꂩ��A ���̂��Ƃɂ��Đ������܂��B
������Ƃ��̑O�ɁA �x�N�g������̊�{�������f�ڂ��Ă����܂��B
�@�@�X�J���[ �F�@
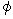
�@�@�x�N�g�� �F�@

�@�@
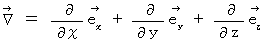 �@�@�@�@�@�@�i �n�~���g�����Z�q �j
�@�@�@�@�@�@�i �n�~���g�����Z�q �j�@�@
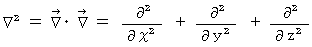 �@�@�@�i ���v���X���Z�q
�@�@�@�i ���v���X���Z�q  �j
�j�@�@���z �F�@
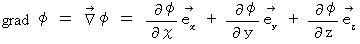
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
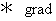 �́A �X�J���[ �� �x�N�g�� �ɕϊ����鉉�Z�q�ł��B
�́A �X�J���[ �� �x�N�g�� �ɕϊ����鉉�Z�q�ł��B�@�@���U �F�@
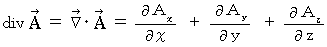
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
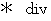 �́A �x�N�g�� �� �X�J���[ �ɕϊ����鉉�Z�q�ł��B
�́A �x�N�g�� �� �X�J���[ �ɕϊ����鉉�Z�q�ł��B�@�@��] �F�@
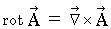
�@�@�@�@�@�@�@�@�@�@�@�@
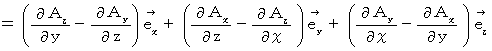
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
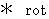 �́A �x�N�g�� �� �x�N�g�� �ɕϊ����鉉�Z�q�ł��B
�́A �x�N�g�� �� �x�N�g�� �ɕϊ����鉉�Z�q�ł��B�@�@�@
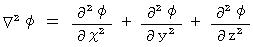
�@�@�@
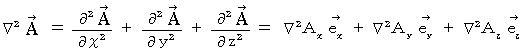
�@ �ł́A �{��ɓ���܂��傤�B �d���C�w�̌����̓}�N�X�E�F���̕������ɂ܂Ƃ߂��Ă��܂��̂ŁA �܂���������n�܂�܂��B
�d�חʂ̑��݂��Ȃ���Ԃɂ�����}�N�X�E�F���̕������i �ڍH�c�P�ʌn �j�F
�@ �@�@�@�@
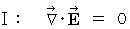
�@�@�@�@�@

�@�@�@�@�@
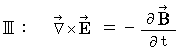
�@�@�@�@�@
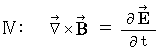
�x�N�g����͂̌��� �� ��
 ���A
���A�@ �@�@�@
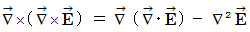
�@�@�@�@�@�@�@�@�@�@�@�@�@
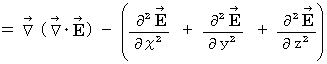
�@�@�@�@�@�@�@�@�@�@�@�@�@
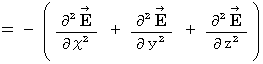 �@�@�@�E �E �E �E �E�i�� 22-3�j
�@�@�@�E �E �E �E �E�i�� 22-3�j��
 �� ��
�� ��  ���A
���A�@ �@�@�@
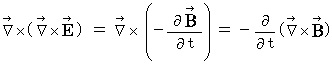
�@�@�@�@�@�@�@�@�@�@�@�@�@
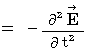 �@�@�@�E �E �E �E �E�i�� 22-4�j
�@�@�@�E �E �E �E �E�i�� 22-4�j�i�� 22-3�j�Ɓi�� 22-4�j���A
�@�@�@�@�@
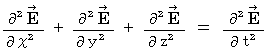
�@�@
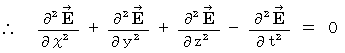
�㎮�𐬕��\������ƁA ���̂悤�ɂȂ�܂��B
�@�@�@�@�@
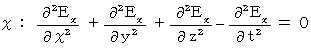
�@�@�@�@�@
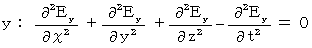
�@�@�@�@�@
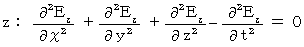
�@�@�@�@�@
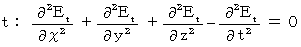
�x�N�g����͂̌��� �� ��
 ���A
���A�@ �@�@�@
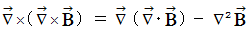
�@�@�@�@�@�@�@�@�@�@�@�@�@
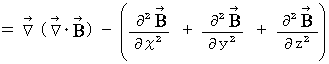
�@�@�@�@�@�@�@�@�@�@�@�@�@
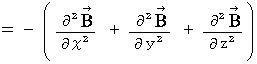 �@�@�@�E �E �E �E �E�i�� 22-5�j
�@�@�@�E �E �E �E �E�i�� 22-5�j��
 �� ��
�� ��  ���A
���A�@ �@�@�@
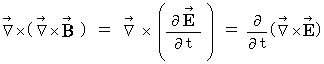
�@�@�@�@�@�@�@�@�@�@�@�@�@
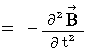 �@�@�@�E �E �E �E �E�i�� 22-6�j
�@�@�@�E �E �E �E �E�i�� 22-6�j�i�� 22-5�j�Ɓi�� 22-6�j���A
�@�@�@�@�@
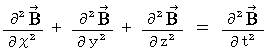
�@�@
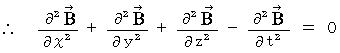
�@�ȏ���A �d�חʂ̑��݂��Ȃ��^�ł́A �d��Ǝ���Ɋւ��āA (�� 22-1�j�Ɓi�� 22-2�j�����藧���Ă��邱�Ƃ��킩��܂����B
�@�i�� 22-1�j��i�� 22-2�j�̎��̌`�́A�u �g�������� �v�ƌ����܂��B �g���������͎��̂悤�Ȍ`�����Ă��܂��B
�@�@�@
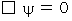
�@�@�@�@�@�@�@�@�@�������A
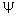 �� �g���� �F
�� �g���� �F�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
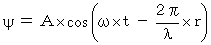
�@�@�@�@�@�@�@�@�@�@�@�@�@�@
 �� �_�����x���V�A�� �F
�� �_�����x���V�A�� �F�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
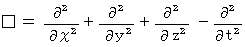
�@ �����ł��Ƃ��A ��Ԃ��y�������ɂ����ɓ`���A ���w�������ɂ̂��U������d���̔g�������������̂悤�ɂ��܂��B
�@�@�@�@
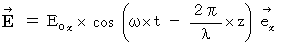
����́A ���̂悤�ɂ��\����܂��B
�@�@�@�@
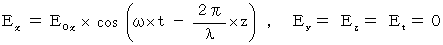
���ꂪ���̎������������Ƃ��ȉ��Ɏ����܂��B
�@�@�@�@�@
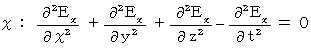
�@�@�@�@�@
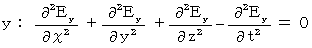
�@�@�@�@�@
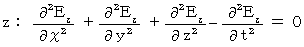
�@�@�@�@�@
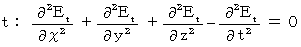
�@ �܂��A �x�C�y�C�s �� �Ɋւ��ẮA
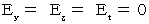 �@��薾�炩�ɐ��藧���Ă��܂��B
�@��薾�炩�ɐ��藧���Ă��܂��B�@ �܂��A �w �� �Ɋւ��ẮA
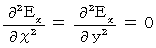 �@�ł�����A ����
�@�ł�����A ����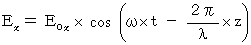 �@���@�@
�@���@�@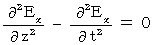 �@�������Ƃ����������킯�ł��B
�@�������Ƃ����������킯�ł��B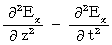
�@�@�@�@�@�@
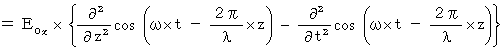
�@�@�@�@�@�@
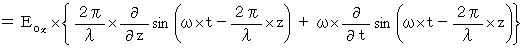
�@�@�@�@�@�@
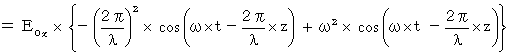
�@�@�@�@�@�@
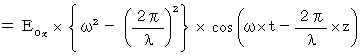
�����ŁA
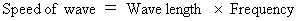 �@���A ���̎������藧���܂��B
�@���A ���̎������藧���܂��B�@�@�@�@�@
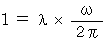 �@�@�@�@�@
�@�@�@�@�@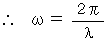
���������āA
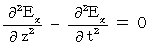 �@�ɂȂ邱�Ƃ��킩��܂��B
�@�ɂȂ邱�Ƃ��킩��܂��B�@ ���ɁA �}�N�X�E�F���������� ��
 ���v���o���Ă��������B �ȉ��ɍČf���܂��B
���v���o���Ă��������B �ȉ��ɍČf���܂��B�@�@�@�@�@
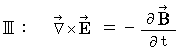
�@ �����ŁA ���̎��Ɂ@
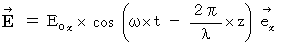 �@�������܂��B
�@�������܂��B����ƁA ���ӂ͎��̂悤�ɂȂ�܂��B
�@ �@�@�@
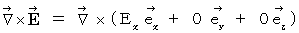
�@�@�@�@�@�@�@�@�@

�@�@�@�@�@�@�@�@�@
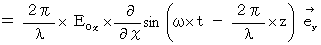
���������āA ���̂悤�ɂȂ�܂��B
�@�@�@�@
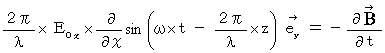
���������āA
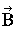 �͎��̂悤�ɂȂ�܂��B
�͎��̂悤�ɂȂ�܂��B�@�@�@�@
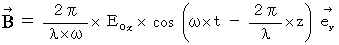
�����ŁA
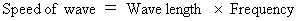 �@���A ���̎������藧���܂��B
�@���A ���̎������藧���܂��B�@�@�@�@
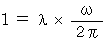
���������āA ���̂悤�ɂȂ�܂��B
�@�@�@�@
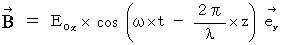
�������āA �������́A ���ǎ��̂Q�̎��܂����B
�@�@�@�@�@�@
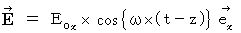
�@�@�@�@�@�@
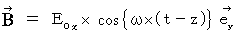
�@ ������
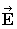 ��
�� 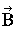 ���A �������͓d���g�̑��݂ɋC�Â��܂��B ����́A �����ʑ��ƐU���̓d��Ǝ��ꂪ���p�����ɐU�����Ȃ���
���A �������͓d���g�̑��݂ɋC�Â��܂��B ����́A �����ʑ��ƐU���̓d��Ǝ��ꂪ���p�����ɐU�����Ȃ���  �̃x�N�g���̕����ɑ���
�̃x�N�g���̕����ɑ���  �ŋ�Ԃ�`���g�ł��B
�ŋ�Ԃ�`���g�ł��B