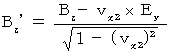(5)マクスウェル方程式の解釈
一般的なマクスウェル方程式は、 次のようなものです。

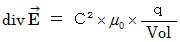

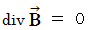

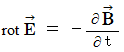

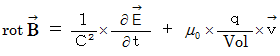
*
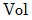 は体積
は体積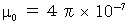 ,
, 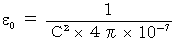
これらを、 実質電場( 電場を光の速さで割ったもの )を使って表すと、 次のようになります。

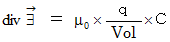

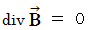

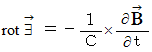

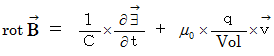
コメント:
-
これらは、
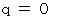 のときは、 次のように表されます。
のときは、 次のように表されます。
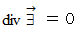

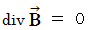

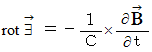

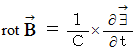
 式の両辺に回転演算子を作用させたものに、
式の両辺に回転演算子を作用させたものに、  と
と  を代入し、
を代入し、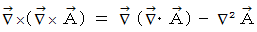 という公式を使うと、 次のようになります。
という公式を使うと、 次のようになります。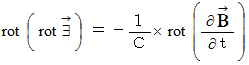
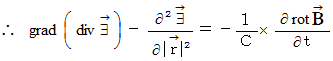
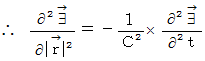
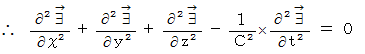
この式は、 波動方程式です。 したがって、 電場は光の速さで伝わる
波のようなものであることがわかります。
一方、 マクスウェル方程式を、 目・工・田 単位系 を用いて、 私バージョンで表すと、 次のようになります。

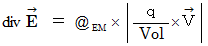

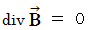

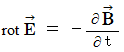

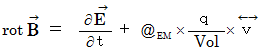
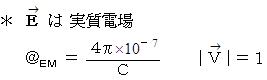
それぞれの式の意味は、 次のようなものです。
 電場を形成する4次元時空間電気量は、 それが存在する微小空間において電場を湧き出している。( 4次元時空間電気量の符号が - のときは、 電場を吸い込んでいる。)その湧き出す( 吸い込む )電場の大きさは、 単位体積あたりの4次元時空間電気量に比例する。( この式は、 クーロン力の定義 や ガウスの法則 を含んでいる。)
電場を形成する4次元時空間電気量は、 それが存在する微小空間において電場を湧き出している。( 4次元時空間電気量の符号が - のときは、 電場を吸い込んでいる。)その湧き出す( 吸い込む )電場の大きさは、 単位体積あたりの4次元時空間電気量に比例する。( この式は、 クーロン力の定義 や ガウスの法則 を含んでいる。) たとえ磁場を形成するものが存在するとしても、 それらは決して、 それが存在する微小空間において磁場を湧き出すことはできない。 したがって、 単極 ( モノポール )の磁場だけを持つ物質は存在しない。
たとえ磁場を形成するものが存在するとしても、 それらは決して、 それが存在する微小空間において磁場を湧き出すことはできない。 したがって、 単極 ( モノポール )の磁場だけを持つ物質は存在しない。 磁場の時間的な変化は、 周囲に電場を形成する。 形成される電場は、 仮想の「 均一の電荷 の集まり 」に対して、 渦を作るような力となる。 その大きさは磁場の変化量に比例する。 また、 その渦の回転によって仮想の目ネジが進む方向は、 磁場のベクトルが変化する方向と逆である。( この式は、 ファラデーの電磁誘導の法則を含んでいる。)
磁場の時間的な変化は、 周囲に電場を形成する。 形成される電場は、 仮想の「 均一の電荷 の集まり 」に対して、 渦を作るような力となる。 その大きさは磁場の変化量に比例する。 また、 その渦の回転によって仮想の目ネジが進む方向は、 磁場のベクトルが変化する方向と逆である。( この式は、 ファラデーの電磁誘導の法則を含んでいる。) 電場の時間的な変化( 変位電流 )は、 周囲に磁場を形成する。 形成される磁場は、 仮想の「 均一の空間電気量 の束 」に対して、 回転させるような力となる。 その大きさは電場の変化量に比例する。 また、 その回転によって仮想の目ネジが進む方向は、 電場のベクトルが変化する方向である。( この式は、 マクスウェルの法則を含んでいる。)
電場の時間的な変化( 変位電流 )は、 周囲に磁場を形成する。 形成される磁場は、 仮想の「 均一の空間電気量 の束 」に対して、 回転させるような力となる。 その大きさは電場の変化量に比例する。 また、 その回転によって仮想の目ネジが進む方向は、 電場のベクトルが変化する方向である。( この式は、 マクスウェルの法則を含んでいる。)また、 相対的空間電気量は、 周囲に磁場を形成する。 形成される磁場たちは、 仮想の「 均一の空間電気量 の束 」に対して、 回転させるような力となる。 その大きさは相対的空間電気量の大きさに比例し、 また、 その回転によって仮想の目ネジが進む方向は、 相対的空間電気量の向きである。( この式は、 アンペールの法則を含んでいる。)
(6)4次元電磁ポテンシャル と マックスウェルの方程式
マクスウェル方程式を電磁場のポテンシャルを使って表現すると、 電場と磁場の統一性がさらにはっきりと見えてきますし、 また、「 4次元時空間 」という発想が生まれてきます。
まず、 簡単に、 電磁場のポテンシャルについて箇条書きをしておきます。
 電荷量の周辺には、 スカラーポテンシャルが発生していています。
電荷量の周辺には、 スカラーポテンシャルが発生していています。 それを「 電位 」または「 静電ポテンシャル 」と言います。
それを「 電位 」または「 静電ポテンシャル 」と言います。 電位は、 電荷量から遠い位置ほど小さくなっています。
電位は、 電荷量から遠い位置ほど小さくなっています。 電位の下り方向の勾配は、 電場になります。
電位の下り方向の勾配は、 電場になります。 相対的空間電気量の周辺には、 ベクトルポテンシャルが発生しています。
相対的空間電気量の周辺には、 ベクトルポテンシャルが発生しています。 それを「 電流ポテンシャル 」と私は言っています。
それを「 電流ポテンシャル 」と私は言っています。 「 電流ポテンシャル 」は、 相対的空間電気量から遠い位置ほど小さくなっています。
「 電流ポテンシャル 」は、 相対的空間電気量から遠い位置ほど小さくなっています。 「 電流ポテンシャル 」の回転は、 磁場になります。
「 電流ポテンシャル 」の回転は、 磁場になります。 静電ポテンシャル と 電流ポテンシャル を組み合わせて、「 4次元電磁ポテンシャル
静電ポテンシャル と 電流ポテンシャル を組み合わせて、「 4次元電磁ポテンシャル(
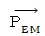 )」と言います。
)」と言います。マクスウェルの4つの方程式は、 電位
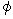 と 電流ポテンシャル
と 電流ポテンシャル 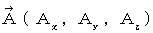 とを用いて、 次の4つの式で表されます。
とを用いて、 次の4つの式で表されます。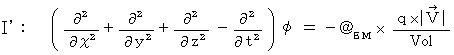
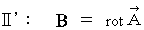
つまり、
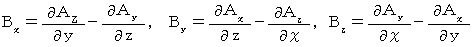
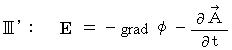
つまり、
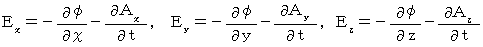
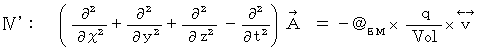
*
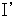 と
と 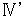 とをまとめると次のようになります。
とをまとめると次のようになります。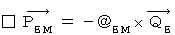
ただし、
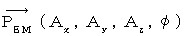
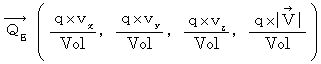
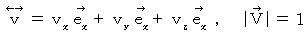
* ダランベルシアン :
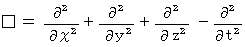 は、 ラプラシアン
は、 ラプラシアン の4次元時空間バージョンです。
の4次元時空間バージョンです。つまり、
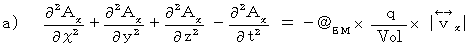
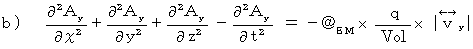
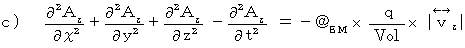
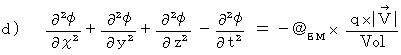
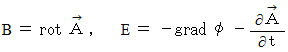 のとき、 ベクトル関数
のとき、 ベクトル関数 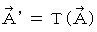 から得られる
から得られる 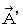 と スカラー関数
と スカラー関数 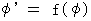 から得られる
から得られる 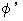 が次の式を満たしているとき、
が次の式を満たしているとき、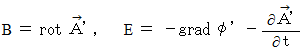
「 ベクトル関数(
 )と スカラー関数(
)と スカラー関数( 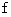 )は、 ゲージ変換 である。」と言います。
)は、 ゲージ変換 である。」と言います。さて、 任意のスカラー関数を
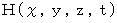 とし、 次のようにしたときに、
とし、 次のようにしたときに、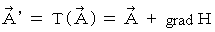
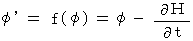
以下のように、
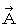 と
と 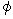 から
から 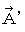 と
と 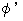 へ変換しても、
へ変換しても、 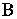 と
と 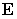 は変化しません。
は変化しません。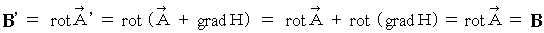
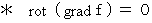 という公式があります。
という公式があります。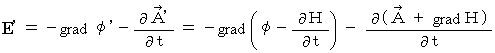
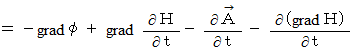
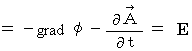
したがって、 この2つの関数
 と
と 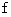 は、 ともにゲージ変換です。
は、 ともにゲージ変換です。ではこれから、 マクウスウェルの方程式がどうして
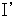 から
から 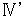 のように表されるのか説明しましょう。
のように表されるのか説明しましょう。最初に、 マクスウェルの方程式を再度記載しておきます。
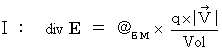
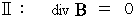
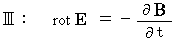
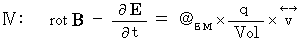
まず、 電流ポテンシャルを
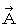 とし、 次の式が成り立つと仮定します。
とし、 次の式が成り立つと仮定します。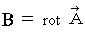 ・ ・ ・ ・(式 22-12)
・ ・ ・ ・(式 22-12)すると、 式
 より、 次のようになります。
より、 次のようになります。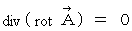
この式は、 ベクトル解析の定理 :
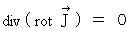 を満足しています。 また、「
を満足しています。 また、「 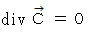 ならば、
ならば、 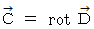 を満たす
を満たす 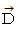 が必ず存在する。」というベクトル解析の定理も存在します。 したがって、(式 22-12)は 式
が必ず存在する。」というベクトル解析の定理も存在します。 したがって、(式 22-12)は 式  に相当する式であることがわかります。
に相当する式であることがわかります。また、 式
 と(式 22-12)より、 次の式が導かれます。
と(式 22-12)より、 次の式が導かれます。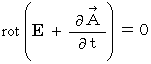
すると、
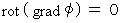 という公式から、 次の式が導かれます。
という公式から、 次の式が導かれます。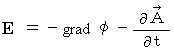 ・ ・ ・ ・(式 22-13)
・ ・ ・ ・(式 22-13)ここで、 電磁気学の公式 :
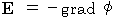 より、(式 22-13)の
より、(式 22-13)の 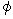 は電位であることがわかります。 すると、(式 22-13)から、 私たちは次のことを知ります。
は電位であることがわかります。 すると、(式 22-13)から、 私たちは次のことを知ります。「 電場は、 電位の勾配だけで作られているのではなく、 電流ポテンシャルの
時間的変化によっても作られている。」
(式 22-12)と(式 22-13)の
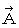 と
と 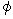 を
を 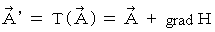 から得られる
から得られる 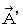 と
と 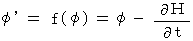 から得られる
から得られる 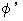 に置き換えても、
に置き換えても、 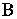 や
や 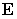 が変化しないことは前述したとおりです。
が変化しないことは前述したとおりです。そして、 マクスウェルの方程式の 式
 と 式
と 式  は、
は、 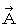 と
と 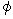 を用いて、 それぞれ次のように表すことができます。
を用いて、 それぞれ次のように表すことができます。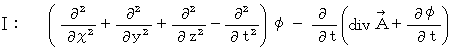
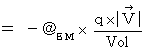 ・ ・ ・ ・(式 22-11)
・ ・ ・ ・(式 22-11)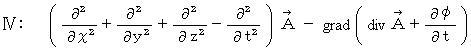
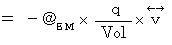 ・ ・ ・(式 22-14)
・ ・ ・(式 22-14)式
 の導き方は、 以下のごとしです。
の導き方は、 以下のごとしです。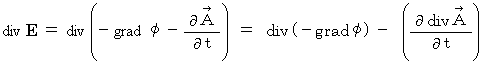
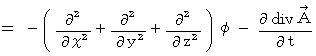
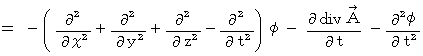
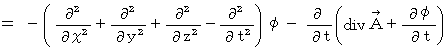
式
 の導き方は、 以下のごとしです。
の導き方は、 以下のごとしです。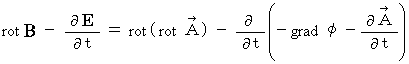
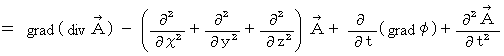
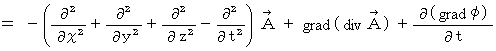
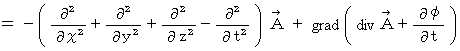
もし、
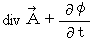 が
が  であれば、(式22-11)と(式22-14)はよく似た形になります。
であれば、(式22-11)と(式22-14)はよく似た形になります。そこで
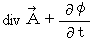 について考えます。
について考えます。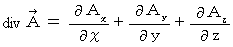 ですので、 4次元ベクトル
ですので、 4次元ベクトル 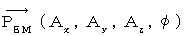 を考え、 次のように表します。
を考え、 次のように表します。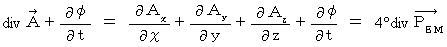
この4次元ベクトル
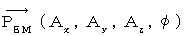 は、「 4次元電磁ポテンシャル 」と言われます。 4次元電磁ポテンシャルは、 電流ポテンシャル と 静電ポテンシャル を組み合わせた4次元ベクトルです。
は、「 4次元電磁ポテンシャル 」と言われます。 4次元電磁ポテンシャルは、 電流ポテンシャル と 静電ポテンシャル を組み合わせた4次元ベクトルです。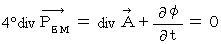 と仮定すると、 マクスウェル方程式に相当する(式 22-11)~(式 22-14)は次のようなります。
と仮定すると、 マクスウェル方程式に相当する(式 22-11)~(式 22-14)は次のようなります。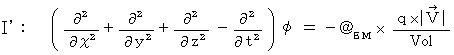
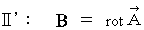
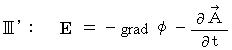
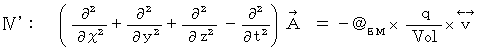
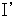 と
と 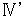 とをまとめると次のようになります。
とをまとめると次のようになります。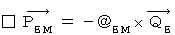
ただし、
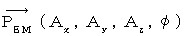
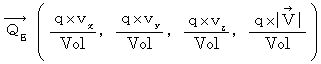
私は、 この式を「 湧き出し0の4次元電磁ポテンシャルによる電磁気学
の基礎方程式 」と言っています。
これから、
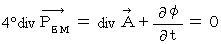 という仮定に矛盾がないかどうか見ていきましょう。
という仮定に矛盾がないかどうか見ていきましょう。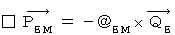 より、
より、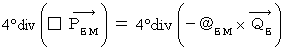
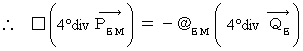 ・ ・ ・ ・ ・(式 22-15)
・ ・ ・ ・ ・(式 22-15)ところで、 マクスウェル方程式
 の両辺の発散をとると次のようになります。
の両辺の発散をとると次のようになります。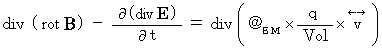
定理から
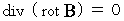 ですので、 これと 式
ですので、 これと 式  を 上式に代入すると、
を 上式に代入すると、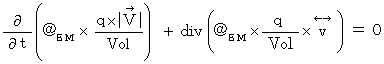
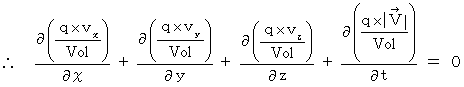
この式は、
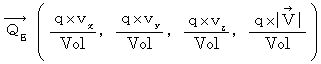 とおくと、 次のように表すことができます。
とおくと、 次のように表すことができます。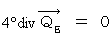 ・ ・ ・ ・ ・(式 22-16)
・ ・ ・ ・ ・(式 22-16)この式は、 一般に「 電荷保存法則 」と言われますが、私は「 4次元電気量密度湧き出し0の法則 」と言っています。また、私は
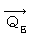 を「 4次元電気量密度 」と言っています。
を「 4次元電気量密度 」と言っています。(式 22-16)を(式 22-15)に代入すると、 次の式が得られます。
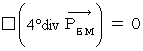
では、 実際にこの式の左辺が
 になるかどうか見ていきましょう。
になるかどうか見ていきましょう。 まず、 左辺を展開します。
まず、 左辺を展開します。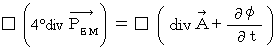
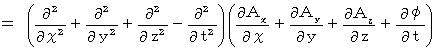
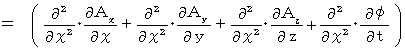
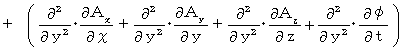
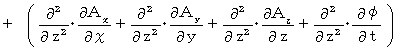
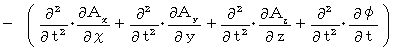
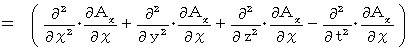
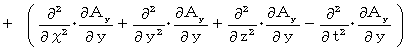
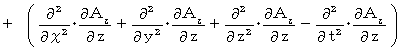
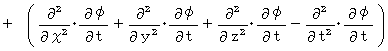
 次に、
次に、 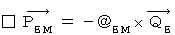 の成分表示の式たちを加工します。
の成分表示の式たちを加工します。湧き出し0の4次元電磁ポテンシャルによる電磁気学の基本方程式の X 軸成分の両辺を χ で微分すると、
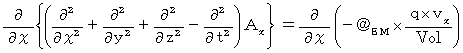
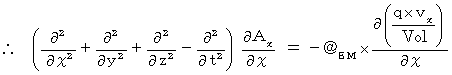
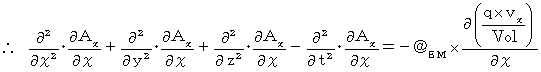
湧き出し0の4次元電磁ポテンシャルによる電磁気学の基本方程式の Y 軸成分の両辺を y で微分すると、
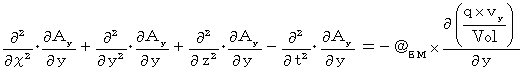
湧き出し0の4次元電磁ポテンシャルによる電磁気学の基本方程式の Z 軸成分の両辺を z で微分すると、
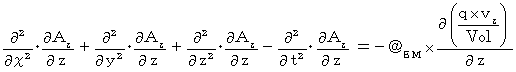
湧き出し0の4次元電磁ポテンシャルによる電磁気学の基本方程式の T 軸成分の両辺を t で微分すると、
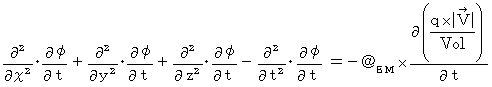

 で得られた4つの式たちを
で得られた4つの式たちを  に代入します。
に代入します。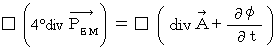
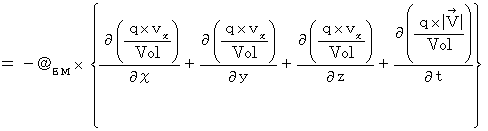
4次元電気量密度湧き出し0の法則 :
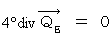
つまり、
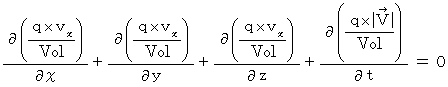 より、
より、結局、 次のようになります。
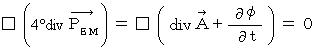
というわけで、
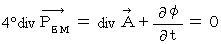 という仮定の式に矛盾はありませんでした。 そこで、 この式を採択することにします。 この式は、 一般に「 ローレンツ条件 」とか「 ローレンツゲージ 」と言われています。 私はこれを「 4次元電磁ポテンシャル湧き出し0の条件 」と言っています。
という仮定の式に矛盾はありませんでした。 そこで、 この式を採択することにします。 この式は、 一般に「 ローレンツ条件 」とか「 ローレンツゲージ 」と言われています。 私はこれを「 4次元電磁ポテンシャル湧き出し0の条件 」と言っています。では、「 ローレンツ条件 」を満たす電磁ポテンシャル
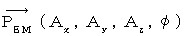 は必ず存在するのでしょうか? そんな
は必ず存在するのでしょうか? そんな 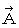 と
と 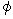 のペアは必ず存在するのでしょうか?
のペアは必ず存在するのでしょうか?そこで、 まず、
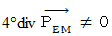 と仮定してみます。
と仮定してみます。そして、 この
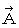 と
と 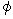 のペアを次のようにゲージ変換してみます。 ゲージ変換ですから、 これによって
のペアを次のようにゲージ変換してみます。 ゲージ変換ですから、 これによって 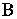 や
や 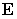 が変化することはありません。
が変化することはありません。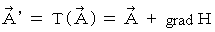 ,
, 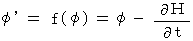
ただし、
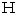 は任意のスカラー関数
は任意のスカラー関数次に、 この
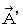 と
と 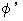 のペアによる4次元電磁ポテンシャル
のペアによる4次元電磁ポテンシャル 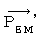 の発散を求めます。
の発散を求めます。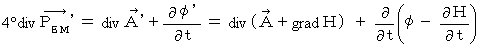
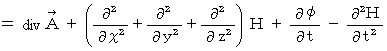
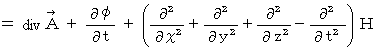
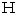 は任意のスカラー関数ですので、 以下の条件を満たす
は任意のスカラー関数ですので、 以下の条件を満たす 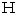 を選んでやると、
を選んでやると、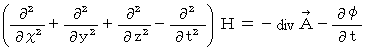
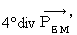 は必ず
は必ず  になります。
になります。以上より、 湧き出し0の4次元電磁ポテンシャルが必ず存在することがわかりました。 したがって、 どんな場合でも、 電磁場のポテンシャルを用いてマクスウェルの方程式を表すことが可能であることがわかりました。
湧き出し0の4次元電磁ポテンシャルによる電磁気学の基本方程式は、 ローレンツ変換にて共変性があります。 つまりローレンツ変換にてその形を変えません。 なぜならば、 マクスウェル方程式の共変性を保証する座標変換を求めて発見されたのが、 ローレンツ変換だからです。
電荷量の存在しない空間では、 湧き出し0の4次元電磁ポテンシャルによる電磁気学の基本方程式は、 波動方程式になります。
(7)複素数電磁場テンソルの起源
マクスウェルの4つの方程式は、 静電場のスカラーポテンシャル( 電位
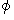 )と 磁場のベクトルポテンシャル
)と 磁場のベクトルポテンシャル 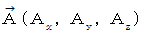 とを用いて、 4つの式で表されることを先に述べました。
とを用いて、 4つの式で表されることを先に述べました。 これから、 そのうち2つの式を用いて考えていきます。 それは、 マクスウェルの 式Ⅱ と 式Ⅲ に相当する次の式たちです。
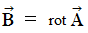 ・ ・ ・ ・(式 2271)
・ ・ ・ ・(式 2271)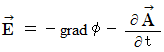 ・ ・ ・ ・(式 2272)
・ ・ ・ ・(式 2272)1番目に、(式 2271)は、 次のように表されます。
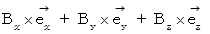
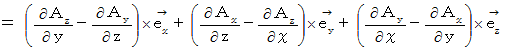
したがって、 次のようになります。
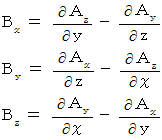
ここで、 次のように置きます。
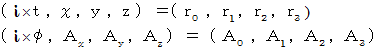
コメント : ここでは、「 複素数4次元電磁ポテンシャル 」
を次のように表します。
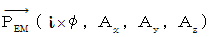
また、 次のような2階のテンソルを考えます。
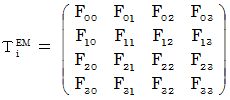
そして、 右のように置きます。
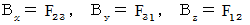
すると、 次のようになります。
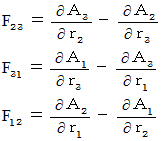
したがって、 この3つの式たちは、 次の式に含まれることがわかります。
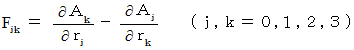 ・ ・ ・ ・(式 2273)
・ ・ ・ ・(式 2273)さて、(式 2273)より次の式が成り立ちます。
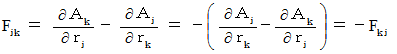
2番目に、(式 2272):
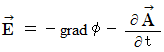 は次のよう表されます。
は次のよう表されます。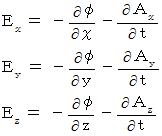
ここで、 右のように置きます。
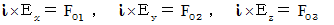
すると、 次のようになります。
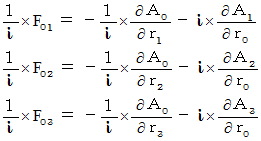
この3つの式たちは、 それぞれ次のように変形されます。
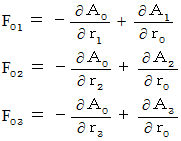
よって、 この3つの式たちは、 それぞれ次のように変形されます。
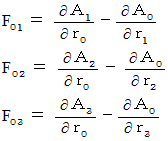
したがって、 この3つの式たちは、 次の式にまとめることができます。
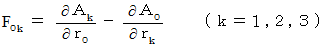
この式は、(式 2273):
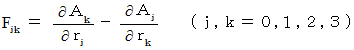 に含まれます。
に含まれます。3番目に、 以上から、
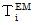 は次のようになります。
は次のようになります。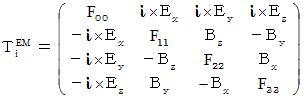
こういうタイプのテンソルは、「 反対称テンソル 」と言われます。
そうして、 最後に
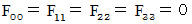 として、 でき上がったのが、「 複素数電磁場テンソル
として、 でき上がったのが、「 複素数電磁場テンソル 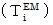 」です。
」です。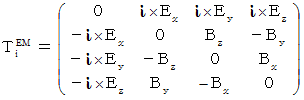
(8)マクスウェル方程式から導かれたローレンツ変換( ローレンツ変換の起源 )
1904年に、 ローレンツが、 マクスウェルの方程式が座標変換にても成立し続ける、 ローレンツ変換を完成させました。 それは簡単に言うと次のような方法でした。
目・工・田単位系のように光の速さが
 となる単位系では、 マクスウェルの方程式を演算子を用いずに表すと、 次のようになります。
となる単位系では、 マクスウェルの方程式を演算子を用いずに表すと、 次のようになります。【 Ⅰ 式 】
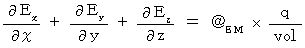 ・ ・ ・ ・ ・(式001)
・ ・ ・ ・ ・(式001)*

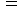
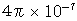
【 Ⅱ 式 】
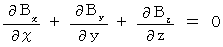 ・ ・ ・ ・ ・(式002)
・ ・ ・ ・ ・(式002)【 Ⅲ 式 】
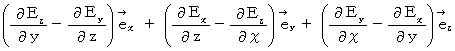
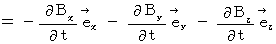
【 Ⅳ 式 】
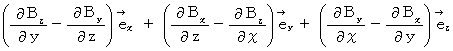
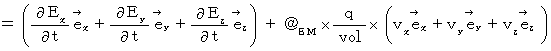
【 Ⅲ 式 】 より、
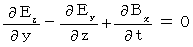 ・ ・ ・ ・ ・(式003)
・ ・ ・ ・ ・(式003)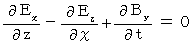 ・ ・ ・ ・ ・(式004)
・ ・ ・ ・ ・(式004)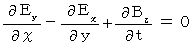 ・ ・ ・ ・ ・(式005)
・ ・ ・ ・ ・(式005)【 Ⅳ 式 】 より、
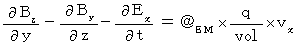 ・ ・ ・ ・ ・(式006)
・ ・ ・ ・ ・(式006)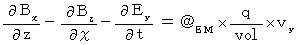 ・ ・ ・ ・ ・(式007)
・ ・ ・ ・ ・(式007)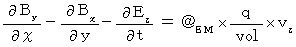 ・ ・ ・ ・ ・(式008)
・ ・ ・ ・ ・(式008)以上は、 第2観察者の座標系
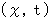 であるとします。 ここで、 第2観察者に対してχ軸方向へ速さ
であるとします。 ここで、 第2観察者に対してχ軸方向へ速さ 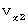 で移動している第1観察者の座標系
で移動している第1観察者の座標系 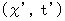 を考えます。 相対性原理により、 そこでもマクスウェルの方程式は成り立ちます。 そこで、 第1観察者の座標系におけるマクスウェル方程式を次のように表します。
を考えます。 相対性原理により、 そこでもマクスウェルの方程式は成り立ちます。 そこで、 第1観察者の座標系におけるマクスウェル方程式を次のように表します。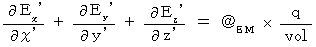 ・ ・ ・ ・ ・(式101)
・ ・ ・ ・ ・(式101)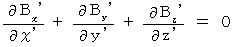 ・ ・ ・ ・ ・(式102)
・ ・ ・ ・ ・(式102)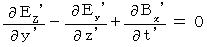 ・ ・ ・ ・ ・(式103)
・ ・ ・ ・ ・(式103)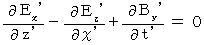 ・ ・ ・ ・ ・(式104)
・ ・ ・ ・ ・(式104)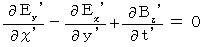 ・ ・ ・ ・ ・(式105)
・ ・ ・ ・ ・(式105)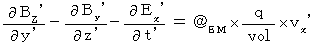 ・ ・ ・ ・ ・(式106)
・ ・ ・ ・ ・(式106)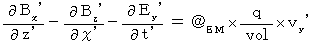 ・ ・ ・ ・ ・(式107)
・ ・ ・ ・ ・(式107)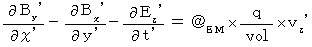 ・ ・ ・ ・ ・(式108)
・ ・ ・ ・ ・(式108)では、 第2観察者の座標系
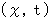 から第1観察者の座標系
から第1観察者の座標系 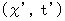 への座標変換式を求めてみましょう。 座標変換は線形変換であること、 また、 静止系において
への座標変換式を求めてみましょう。 座標変換は線形変換であること、 また、 静止系において 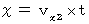 を満たす時空点は、 運動系の空間原点が存在する時空点に座標変換されることより、 この座標変換を次のように書くことができます。
を満たす時空点は、 運動系の空間原点が存在する時空点に座標変換されることより、 この座標変換を次のように書くことができます。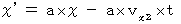 ・ ・ ・ ・ ・(式400)
・ ・ ・ ・ ・(式400)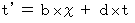 ・ ・ ・ ・ ・(式401)
・ ・ ・ ・ ・(式401)すると、 次の式たちが成り立ちます。
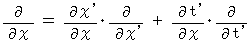
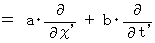 ・ ・ ・ ・ ・(式009)
・ ・ ・ ・ ・(式009)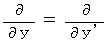 ・ ・ ・ ・ ・(式010)
・ ・ ・ ・ ・(式010)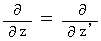 ・ ・ ・ ・ ・(式011)
・ ・ ・ ・ ・(式011)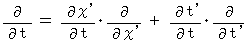
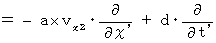 ・ ・ ・ ・ ・(式012)
・ ・ ・ ・ ・(式012)(式009)、(式010)、(式011)を (式001)に代入して、
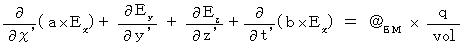
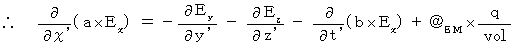
・ ・ ・ ・ ・(式201)
(式009)、(式010)、(式011)を (式002)に代入して、
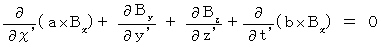
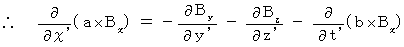
・ ・ ・ ・ ・(式202)
(式010)、(式011)、(式012)を (式003)に代入して、
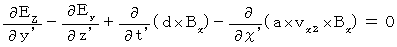
・ ・ ・ ・ ・(式203)
(式009)、(式011)、(式012)を (式004)に代入して、
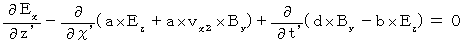
・ ・ ・ ・ ・(式204)
(式009)、(式010)、(式012)を (式005)に代入して、
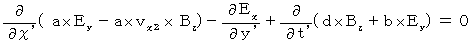
・ ・ ・ ・ ・(式205)
(式010)、(式011)、(式012)を (式006)に代入して、
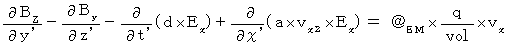
・ ・ ・ ・ ・(式206)
(式009)、(式011)、(式012)を (式007)に代入して、
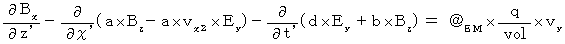
・ ・ ・ ・ ・(式207)
(式009)、(式010)、(式012)を (式008)に代入して、
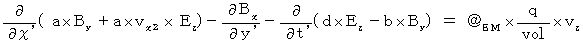
・ ・ ・ ・ ・(式208)
次の式たちを比較することによって、 下の(式314)~(式338)の式を得ます。
(式204)と(式104)、(式205)と(式105)、(式207)と(式107)、(式208)と(式108)
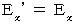 ・ ・ ・ ・ ・(式314)
・ ・ ・ ・ ・(式314)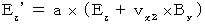 ・ ・ ・ ・ ・(式324)
・ ・ ・ ・ ・(式324)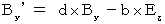 ・ ・ ・ ・ ・(式334)
・ ・ ・ ・ ・(式334)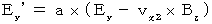 ・ ・ ・ ・ ・(式315)
・ ・ ・ ・ ・(式315)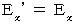 ・ ・ ・ ・ ・(式325)
・ ・ ・ ・ ・(式325)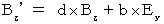 ・ ・ ・ ・ ・(式335)
・ ・ ・ ・ ・(式335)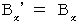 ・ ・ ・ ・ ・(式317)
・ ・ ・ ・ ・(式317)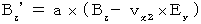 ・ ・ ・ ・ ・(式327)
・ ・ ・ ・ ・(式327)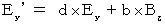 ・ ・ ・ ・ ・(式337)
・ ・ ・ ・ ・(式337)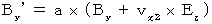 ・ ・ ・ ・ ・(式318)
・ ・ ・ ・ ・(式318)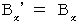 ・ ・ ・ ・ ・(式328)
・ ・ ・ ・ ・(式328)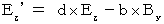 ・ ・ ・ ・ ・(式338)
・ ・ ・ ・ ・(式338)(式315)と(式337)より、
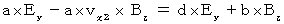
(式324)と(式338)より、
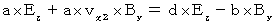
(式334)と(式318)より、
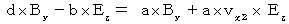
(式335)と(式327)より、
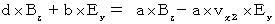
上の4つの式たちより、
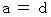 ・ ・ ・ ・ ・(式402)
・ ・ ・ ・ ・(式402)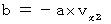 ・ ・ ・ ・ ・(式403)
・ ・ ・ ・ ・(式403)ここで、(式202)を(式203)に代入すると、 次のようになります。
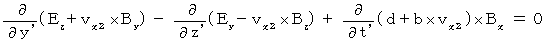
この式に(式324)、(式315)、(式317)を代入すると、 次の式が得られます。
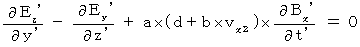
この式と(式103)とを比較すると、
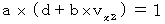
そこで、 この式に、(式402)と(式403)を代入すると、
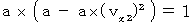
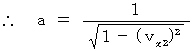 ・ ・ ・ ・ ・(式404)
・ ・ ・ ・ ・(式404)(式404)を(式402)に代入して、
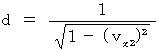
(式402)を(式403)に代入して、
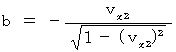
したがって、(式400)と(式401)は、 次のようになります。
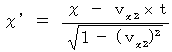
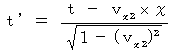
これらの式が、「 マクスウェルの方程式はどの慣性系でも成り立つ。 」という公理から導かれた座標変換です。 この座標変換が「 ローレンツ変換 」です。
また、 ローレンツ変換の導入の過程で、 次のような「 電場と磁場の座標変換方式 」が存在していることもわかります。
(式314):
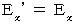
(式315)より、
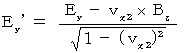
(式324)より、
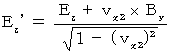
(式317):
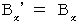
(式318)より、
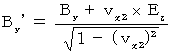
(式327)より、